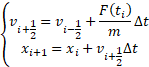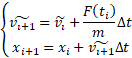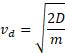"Численные методы интегрирования уравнений движения для одномерной линейной цепочки и частицы в потенциальной яме Леннарда-Джонса" — различия между версиями
(Новая страница: «'''''Курсовой проект по Механике дискретных сред''''' '''Исполни…») |
Totamonik (обсуждение | вклад) (→1. Одномерная линейная цепочка) |
||
| (не показано 10 промежуточных версий этого же участника) | |||
| Строка 8: | Строка 8: | ||
==Постановка задачи:== | ==Постановка задачи:== | ||
| − | # Сравнить различные методы интегрирования уравнений движения (Верле, Рунге-Кутта 4 порядка). Реализовать фиксированные, свободные и периодические условия | + | # Сравнить различные методы интегрирования уравнений движения (Верле, Рунге-Кутта 4 порядка). Реализовать фиксированные, свободные и периодические условия |
# Численно определить скорость диссоциации частицы в потенциальной яме Леннарда-Джонса | # Численно определить скорость диссоциации частицы в потенциальной яме Леннарда-Джонса | ||
==Теоретическая сводка:== | ==Теоретическая сводка:== | ||
| − | + | ==== 1. Одномерная линейная цепочка ==== | |
Рассмотрим модель колебаний одинаковых атомов массой m, находящихся в одномерной цепочке. Пусть в этой цепочке находится N атомов, связанных между собой квазиупругой силой с коэффициентом упругости k. | Рассмотрим модель колебаний одинаковых атомов массой m, находящихся в одномерной цепочке. Пусть в этой цепочке находится N атомов, связанных между собой квазиупругой силой с коэффициентом упругости k. | ||
| − | [[Image: | + | [[Image:Изображение22331.png|top]] |
| − | + | Если учитывать взаимодействие только соседних атомов, уравнение движения можно записать в следующем виде: | |
| − | + | [[Image:Изображение22333.png|top]] | |
| − | |||
| + | Для решения уравнения движения воспользуемся численными методами интегрирования: | ||
| − | + | а. Метод Верле | |
| + | [[Image:Изображение151.png|top]] | ||
| + | |||
| + | Введем обозначения: | ||
| + | |||
| + | [[Image:Изображение1512.png|top]] | ||
| + | |||
| + | Тогда для численной реализации удобно записать: | ||
| + | |||
| + | [[Image:Изображение1513.png|top]] | ||
| − | |||
б. Метод Рунге-Кутта 4 порядка | б. Метод Рунге-Кутта 4 порядка | ||
| − | + | [[Image:Изображение22334.png|top]] | |
| − | |||
| − | |||
| − | + | [[Image:Изображение22335.png|top]] | |
| − | + | [[Image:Изображение22336.png|top]] | |
| − | + | [[Image:Изображение22337.png|top]] | |
| − | + | [[Image:Изображение22338.png|top]] | |
| − | + | [[Image:Изображение22339.png|top]] | |
| − | + | [[Image:Изображение223310.png|top]] | |
| − | + | [[Image:Изображение223311.png|top]] | |
| − | + | [[Image:Изображение223312.png|top]] | |
| + | [[Image:Изображение223313.png|top]] | ||
| − | + | [[Image:Изображение223314.png|top]] | |
| + | [[Image:Изображение223315.png|top]] | ||
| − | + | Для каждого из методов реализуются 3 вида граничных условий: | |
| − | + | * Фиксированные граничные условия | |
| − | + | [[Image:Изображение223316.png|top]] | |
| − | + | [[Image:Изображение223317.png|top]] | |
| − | + | [[Image:Изображение223318.png|top]] | |
| + | [[Image:Изображение223319.png|top]] | ||
| − | + | * Свободные граничные условия | |
| + | [[Image:Изображение223320.png|top]] | ||
| + | [[Image:Изображение223321.png|top]] | ||
| − | + | * Периодические граничные условия | |
| − | + | [[Image:Изображение223322.png|top]] | |
| − | + | [[Image:Изображение223323.png|top]] | |
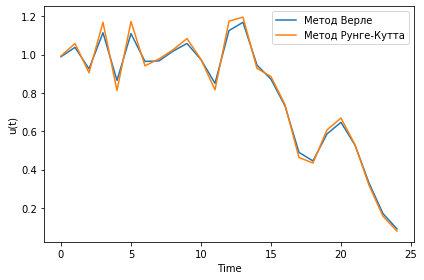
| + | Случай с закрепленными краями: | ||
| − | + | [[Image:Изображение155100.png|top]] | |
| + | Случай с периодическими граничными условиями: | ||
| + | [[Image:Изображение1551p.png|top]] | ||
| − | + | Случай со свободными краями: | |
| − | + | [[Image:Изображение1551f.png|top]] | |
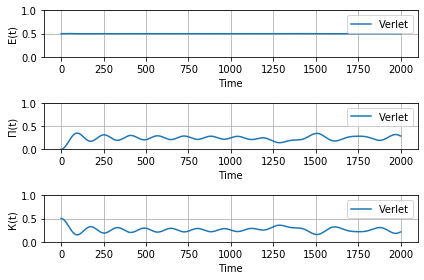
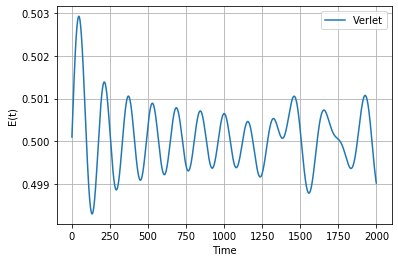
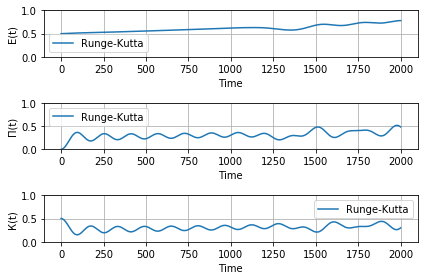
| − | + | Распределение энергии: | |
| + | [[Image:Изображение27015.png|top]] | ||
| − | + | [[Image:Изображение28011.png|top]] | |
| + | [[Image:Изображение27016.png|top]] | ||
| + | ====2. Частица в потенциальной яме Леннарда-Джонса ==== | ||
Уравнение движения частицы в потенциальной яме Леннарда-Джонса: | Уравнение движения частицы в потенциальной яме Леннарда-Джонса: | ||
| − | + | [[Image:Изображение223324.png|top]] | |
| − | + | [[Image:Изображение223325.png|top]] | |
| − | [[Image: | + | [[Image:Изображение223326.png|top]] |
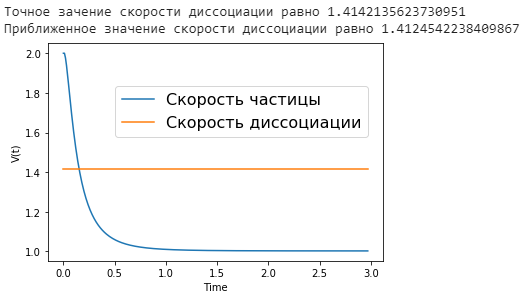
Скоростью диссоциации будем называть скорость, которую необходимо сообщить частице, чтобы она улетела на бесконечность. | Скоростью диссоциации будем называть скорость, которую необходимо сообщить частице, чтобы она улетела на бесконечность. | ||
| − | [[Image: | + | [[Image:Изображение223327.png|top]] |
| − | + | [[Image:Изображение2331.PNG|top]] | |
| − | Вывод: | + | ==Вывод:== |
| − | + | * Были реализованы различные методы интегрирования уравнения движения одномерной линейной цепочки. Заметим, что метод Верле является симплектическим и сохраняет энергию, в то время как метод Рунге-Кутта энергию не сохраняет. | |
| + | * Была численно найдена скорость диссоциации частицы в потенциальной яме Леннарда-Джонса, которая с заданной точностью совпала с теоретическим значением. | ||
Текущая версия на 11:01, 28 января 2020
Курсовой проект по Механике дискретных сред
Исполнитель: Троцкая Валерия
Группа: 3630103/60101
Семестр: осенний семестр 2019-2020 учебного года
Содержание
Постановка задачи:[править]
- Сравнить различные методы интегрирования уравнений движения (Верле, Рунге-Кутта 4 порядка). Реализовать фиксированные, свободные и периодические условия
- Численно определить скорость диссоциации частицы в потенциальной яме Леннарда-Джонса
Теоретическая сводка:[править]
1. Одномерная линейная цепочка[править]
Рассмотрим модель колебаний одинаковых атомов массой m, находящихся в одномерной цепочке. Пусть в этой цепочке находится N атомов, связанных между собой квазиупругой силой с коэффициентом упругости k.
Если учитывать взаимодействие только соседних атомов, уравнение движения можно записать в следующем виде:
Для решения уравнения движения воспользуемся численными методами интегрирования:
а. Метод Верле
Введем обозначения:
Тогда для численной реализации удобно записать:
б. Метод Рунге-Кутта 4 порядка
Для каждого из методов реализуются 3 вида граничных условий:
- Фиксированные граничные условия
- Свободные граничные условия
- Периодические граничные условия
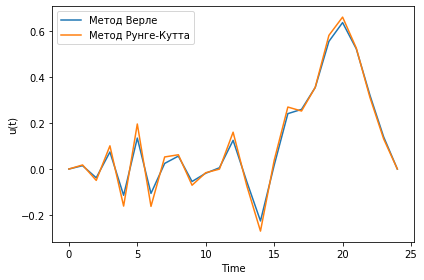
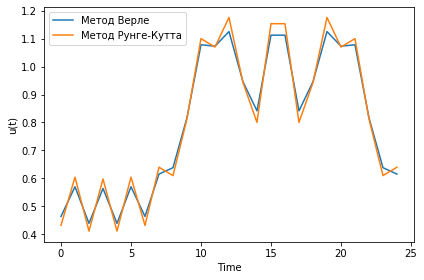
Случай с закрепленными краями:
Случай с периодическими граничными условиями:
Случай со свободными краями:
Распределение энергии:
2. Частица в потенциальной яме Леннарда-Джонса[править]
Уравнение движения частицы в потенциальной яме Леннарда-Джонса:
Скоростью диссоциации будем называть скорость, которую необходимо сообщить частице, чтобы она улетела на бесконечность.
Вывод:[править]
- Были реализованы различные методы интегрирования уравнения движения одномерной линейной цепочки. Заметим, что метод Верле является симплектическим и сохраняет энергию, в то время как метод Рунге-Кутта энергию не сохраняет.
- Была численно найдена скорость диссоциации частицы в потенциальной яме Леннарда-Джонса, которая с заданной точностью совпала с теоретическим значением.