"Одномерная линейная цепочка" — различия между версиями
Catvicaf (обсуждение | вклад) |
|||
| (не показано 16 промежуточных версий 2 участников) | |||
| Строка 8: | Строка 8: | ||
==Постановка задачи== | ==Постановка задачи== | ||
| − | Сравнить различные методы интегрирования уравнений движения одномерной линейной цепочки (Верле, Рунге-Кутта). | + | 1) Сравнить различные методы интегрирования уравнений движения одномерной линейной цепочки (Верле, Рунге-Кутта). |
| + | Реализовать фиксированные, свободные и периодические граничные условия. | ||
| + | |||
| + | 2) Рассмотреть движение частицы в потенциальной яме Леннарда-Джонса: численно определить скорость диссоциации. | ||
| + | |||
| + | ==Первая задача== | ||
| − | + | ===Первая задача: решение=== | |
Уравнение движения: | Уравнение движения: | ||
| + | |||
<math> \dot{v} = w^2 (x_{i+1} - 2x_{i} + x_{i-1}) </math><br> | <math> \dot{v} = w^2 (x_{i+1} - 2x_{i} + x_{i-1}) </math><br> | ||
| − | |||
<math> \dot{x} = v </math><br> | <math> \dot{x} = v </math><br> | ||
| − | === | + | ===Первая задача: метод Верле=== |
<math> v_{i+1} = v_i + w^2 (x_{i+1} - 2x_{i} + x_{i-1})\Delta t </math><br> | <math> v_{i+1} = v_i + w^2 (x_{i+1} - 2x_{i} + x_{i-1})\Delta t </math><br> | ||
<math> x_{i+1} = x_i + v_{i+1}\Delta t </math><br> | <math> x_{i+1} = x_i + v_{i+1}\Delta t </math><br> | ||
| + | |||
| + | |||
| + | ===Первая задача: метод Рунге-Кутта 4 порядка=== | ||
| + | <math> v_{i+1} = v_i + \frac {g_1 + 2g_2+2g_3+g_4}{6}</math><br> | ||
| + | <math> x_{i+1} = x_i + \frac {k_1 + 2k_2+2k_3+k_4}{6}</math><br> | ||
| + | |||
| + | Где | ||
| + | |||
| + | <math> v_{i+1} = v_i + \frac {g_1 + 2g_2+2g_3+g_4}{6}</math><br> | ||
| + | |||
| + | ===Первая задача: дополнительные данные=== | ||
| + | |||
| + | Коэффициент упругости: | ||
| + | <math> c = 1.</math><br> | ||
| + | |||
| + | Масса: | ||
| + | <math> m = 1.</math><br> | ||
| + | |||
| + | Частице под номером 5 задавали перемещение равное 1. | ||
| + | |||
| + | ===Первая задача: результат=== | ||
| + | |||
| + | Метод Верле с фиксированными границами: | ||
| + | |||
| + | [[File:Nomber1VfixedAll.gif]] | ||
| + | |||
| + | Метод Верле со свободными границами: | ||
| + | |||
| + | [[File:Nomber1Vfree.gif]] | ||
| + | |||
| + | Метод Верле с периодическими граничными условиями: | ||
| + | |||
| + | [[File:Nomber1Vperiod.gif]] | ||
| + | |||
| + | Метод Рунге-Кутта 4 порядка с фиксированными границами: | ||
| + | |||
| + | [[File:Namber1rkFixedAll.gif]] | ||
| + | |||
| + | Метод Рунге-Кутта 4 порядка со свободными границами: | ||
| + | |||
| + | [[File:Namber1rkFreeAll.gif]] | ||
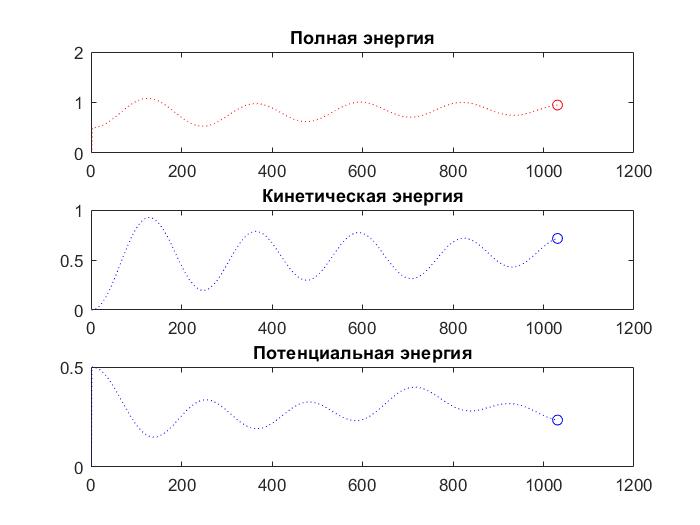
| + | [[File:RkFreeAll.jpg]] | ||
| + | |||
| + | Метод Рунге-Кутта 4 порядка с периодическими граничными условиями: | ||
| + | |||
| + | [[File:Namber1rkPeriod.gif]] | ||
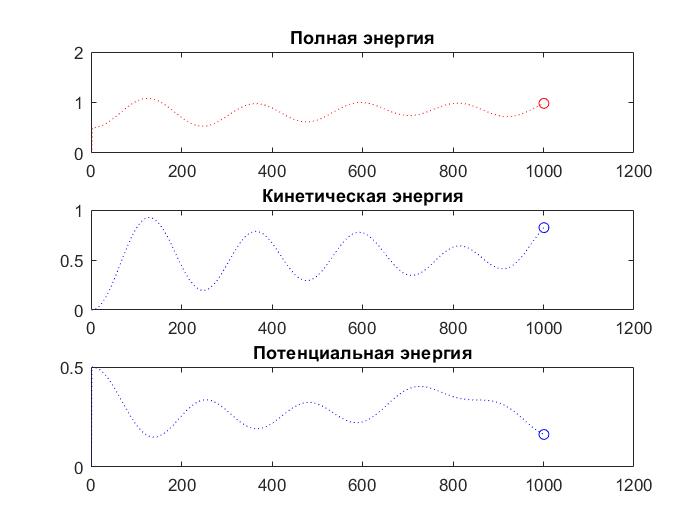
| + | [[File:RkPeriod.jpg]] | ||
| + | |||
| + | ==Вторая задача== | ||
| + | |||
| + | ===Вторая задача: решение=== | ||
| + | Уравнение движения частицы в потенциальной яме Леннарда-Джонса: | ||
| + | |||
| + | <math> v_{i+1} = v_i + F_{r}(x_i)\Delta t </math><br> | ||
| + | <math> x_{i+1} = x_i + v_i \Delta t </math><br> | ||
| + | |||
| + | Где | ||
| + | |||
| + | <math> F_{r}(x_i) = \frac{12D(-(\frac{a}{x})^{13} + (\frac{a}{x})^{7})}{a}</math><br> | ||
Текущая версия на 00:01, 22 января 2020
Курсовой проект по Механике дискретных сред
Исполнитель: Кравченко Ирина
Группа: 3630103/60101
Семестр: осень 2019
Содержание
Постановка задачи[править]
1) Сравнить различные методы интегрирования уравнений движения одномерной линейной цепочки (Верле, Рунге-Кутта). Реализовать фиксированные, свободные и периодические граничные условия.
2) Рассмотреть движение частицы в потенциальной яме Леннарда-Джонса: численно определить скорость диссоциации.
Первая задача[править]
Первая задача: решение[править]
Уравнение движения:
Первая задача: метод Верле[править]
Первая задача: метод Рунге-Кутта 4 порядка[править]
Где
Первая задача: дополнительные данные[править]
Коэффициент упругости:
Масса:
Частице под номером 5 задавали перемещение равное 1.
Первая задача: результат[править]
Метод Верле с фиксированными границами:
Метод Верле со свободными границами:
Метод Верле с периодическими граничными условиями:
Метод Рунге-Кутта 4 порядка с фиксированными границами:
Метод Рунге-Кутта 4 порядка со свободными границами:
Метод Рунге-Кутта 4 порядка с периодическими граничными условиями:
Вторая задача[править]
Вторая задача: решение[править]
Уравнение движения частицы в потенциальной яме Леннарда-Джонса:
Где