Динамическая потеря устойчивости цепочки частиц, соединенных линейными пружинами и имеющими изгибную жесткость — различия между версиями
Bars-ik98 (обсуждение | вклад) |
Bars-ik98 (обсуждение | вклад) (→Построение модели) |
||
| (не показано 6 промежуточных версий этого же участника) | |||
| Строка 21: | Строка 21: | ||
Для решения задачи использовался метод Верле (leapfrog): | Для решения задачи использовался метод Верле (leapfrog): | ||
| − | <math> a_i = F( | + | <math> a_i = F(r_i), </math><br> |
<math> v_{i+\frac {1}{2}} = v_{i-\frac {1}{2}} + a_i dt, </math><br> | <math> v_{i+\frac {1}{2}} = v_{i-\frac {1}{2}} + a_i dt, </math><br> | ||
| − | <math> | + | <math> r_{i+1} = r_{i} + v_{i+\frac {1}{2}} dt</math> |
===Начальные условия=== | ===Начальные условия=== | ||
| Строка 33: | Строка 33: | ||
Левый конец цепочки закреплен, правому задана постоянная скорость.<br> | Левый конец цепочки закреплен, правому задана постоянная скорость.<br> | ||
| − | <math> | + | <math>v_0 = 0</math><br> <math>v_n = -v</math><br> |
===Параметры системы=== | ===Параметры системы=== | ||
| − | Для проведения | + | Для проведения моделирования задаются следующие параметры: |
| − | масса частиц <math> m= | + | масса частиц <math> m=1</math>, жесткость угловой пружины <math> C_s=1</math>, количество частиц в цепочке <math> n=10</math>, равновесная длина пружины <math>{\pmb a_{0}=1}</math>. Остальные параметры системы выражаются через данные. |
===Взаимодействия в системе=== | ===Взаимодействия в системе=== | ||
| Строка 53: | Строка 53: | ||
==Модель== | ==Модель== | ||
В данной программе в начальный момент времени задаются: | В данной программе в начальный момент времени задаются: | ||
| − | *<math> | + | *<math>{\frac{\pmb k}{\pmb C_{s}}}</math> - отношение жесткости линейной пружины к угловой пружине |
| − | *<math> | + | *<math>{\frac{\pmb y_{i}}{\pmb a_{0}}}</math> - отношение начального вертикального смещения к равновесной длине пружины (в процентах) |
| − | *<math>< | + | *<math>{\frac{\pmb v}{\pmb v_{s}}}</math> - отношение скорости правой частицы к <math>{\pmb v_{s}}={\pmb a_{0}}*\sqrt{\frac{\pmb C_{s}}{\pmb m}}</math> |
*Возможность придания скорости левой частице | *Возможность придания скорости левой частице | ||
| − | {{#widget:Iframe|url=http://tm.spbstu.ru/htmlets/VaraevV/Barsik/ | + | {{#widget:Iframe|url=http://tm.spbstu.ru/htmlets/VaraevV/Barsik/HTMLfinal.html|width=850|height=850|border=0}} |
<div class="mw-collapsible mw-collapsed" style="width:100%" > | <div class="mw-collapsible mw-collapsed" style="width:100%" > | ||
| Строка 320: | Строка 320: | ||
</div> | </div> | ||
==Результаты моделирования== | ==Результаты моделирования== | ||
| + | Графики зависимости обезрамеренной продольной силы <math>{\frac{\pmb F_{x}(t)}{\pmb F_{e}}}</math>, где <math>{\pmb F_{е}}</math> - Эйлерова критическая сила в статике, от времени <math>t</math> (от количества итераций) при различных значениях параметров построены в python по данным полученным из программы javascript. | ||
| + | *Как видно из графиков зависимости обезрамеренной продольной силы <math>{\frac{\pmb F_{x}(t)}{\pmb F_{e}}}</math> от времени <math>t</math> (от количества итераций) (Рис. 2 и Рис. 3) линейный участок роста продольной силы имеет наибольшую длину при малых начальных вертикальных смещениях. Следовательно критическая сила, при которой продольная сила перестает расти линейно и начинает уменьшаться, наступает для начального вертикального смещения "<math><1%</math>"относительно равновесной длины пружины <math>{\pmb a_{0}}</math> при большей силе, нежели при начальном смещении "<math><6%</math>" или "<math><11%</math>"относительно равновесной длины пружины <math>{\pmb a_{0}}</math>. | ||
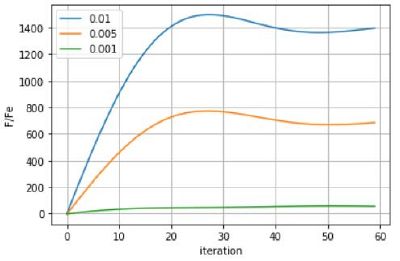
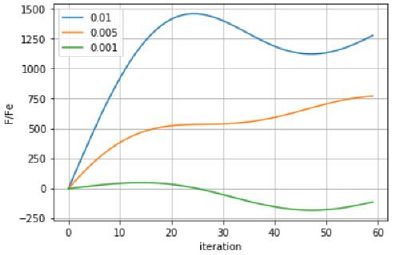
| + | *Из графиков зависимости обезрамеренной продольной силы <math>{\frac{\pmb F_{x}(t)}{\pmb F_{e}}}</math> от времени <math>t</math> (от количества итераций) (Рис. 4, Рис. 5 и Рис. 6) видно, что линейный участок роста продольной силы имеет наибольшую длину при большом значении скорости правой частицы. Это справедливо для любого начального вертикального смещения частиц. Следовательно критическая сила, при которой продольная сила перестает расти линейно и начинает уменьшаться, наступает для скорости правой частицы <math>{\frac{\pmb v}{\pmb v_{s}}=0.01}</math> при большей силе, нежели при скорости правой частицы <math>{\frac{\pmb v}{\pmb v_{s}}=0.005}</math> или <math>{\frac{\pmb v}{\pmb v_{s}}=0.001}</math>. | ||
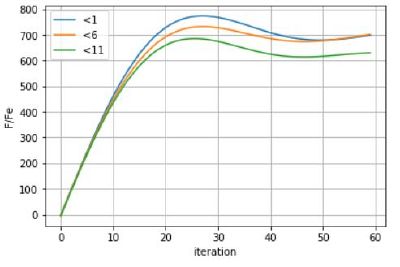
| + | [[Файл:K502.JPG|thumb|Рис.2 Зависимость продольной силы <math>{\frac{\pmb F_{x}(t)}{\pmb F_{e}}}</math> от времени t (от количества итераций) при <math>{\frac{\pmb k}{\pmb C_{s}}=0.5}</math>, при скорости правой частицы <math>{\frac{\pmb v}{\pmb v_{s}}=0.005}</math> и различных начальных вертикальных смещениях.|справа|400px]] | ||
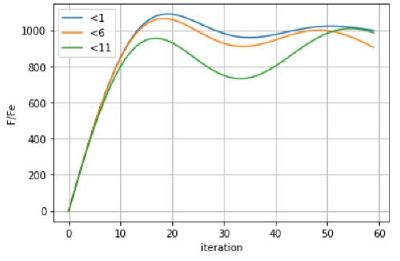
| + | [[Файл:K1000.JPG|thumb|Рис.3 Зависимость продольной силы <math>{\frac{\pmb F_{x}(t)}{\pmb F_{e}}}</math> от времени t (от количества итераций) при <math>{\frac{\pmb k}{\pmb C_{s}}=1}</math>, при скорости правой частицы <math>{\frac{\pmb v}{\pmb v_{s}}=0.005}</math> и различных начальных вертикальных смещениях.|справа|400px]] | ||
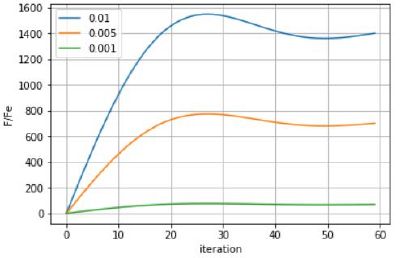
| + | [[Файл:Nachsmesh1.JPG|thumb|Рис.4 Зависимость продольной силы <math>{\frac{\pmb F_{x}(t)}{\pmb F_{e}}}</math> от времени t (от количества итераций) при <math>{\frac{\pmb k}{\pmb C_{s}}=0.5}</math>, начальных вертикальных смещениях <math>{\frac{\pmb y_{i}}{\pmb a_{0}}<1}</math>, при различных скоростях правой частицы.|справа|400px]] | ||
| + | [[Файл:nachsmesh6.JPG|thumb|Рис.5 Зависимость продольной силы <math>{\frac{\pmb F_{x}(t)}{\pmb F_{e}}}</math> от времени t (от количества итераций) при <math>{\frac{\pmb k}{\pmb C_{s}}=0.5}</math>, начальных вертикальных смещениях <math>{\frac{\pmb y_{i}}{\pmb a_{0}}<6}</math>, при различных скоростях правой частицы.|справа|400px]] | ||
| + | [[Файл:Nachsmesh11.JPG|thumb|Рис.6 Зависимость продольной силы <math>{\frac{\pmb F_{x}(t)}{\pmb F_{e}}}</math> от времени t (от количества итераций) при <math>{\frac{\pmb k}{\pmb C_{s}}=0.5}</math>, начальных вертикальных смещениях <math>{\frac{\pmb y_{i}}{\pmb a_{0}}<11}</math>, при различных скоростях правой частицы.|справа|400px]] | ||
| + | ==Ссылки== | ||
| + | *Kuzkin V.A., Dannert M.M.: Dynamic buckling of a column under constant speed compression. Acta Mech (2016) 227:1645-1652. | ||
Текущая версия на 12:40, 17 декабря 2019
Курсовой проект по Механике дискретных сред
Исполнитель: Барсуков Севастьян
Группа: 3630103/60101
Семестр: осень 2019
Содержание
Постановка задачи[править]
Исследовать динамическую потерю устойчивости цепочки частиц, соединенных линейными пружинами и имеющими изгибную жесткость при различных начальных отклонениях, а также при различных скоростях последней частицы.
Построение модели[править]
В данной работе моделирование цепочки проводится методом динамики частиц.
Уравнение движения:
Метод решения[править]
Для решения задачи использовался метод Верле (leapfrog):
Начальные условия[править]
Частицы обладают случайными начальными вертикальными смещениями:
Граничные условия[править]
Левый конец цепочки закреплен, правому задана постоянная скорость.
Параметры системы[править]
Для проведения моделирования задаются следующие параметры: масса частиц , жесткость угловой пружины , количество частиц в цепочке , равновесная длина пружины . Остальные параметры системы выражаются через данные.
Взаимодействия в системе[править]
В системе имеется два типа взаимодействия:
1. Потенциал линейной пружины:
Частицы соединены линейной пружиной:
где k - линейная жесткость пружины; r – расстояние между частицами.
2. Потенциал угловой пружины:
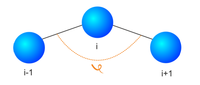
Частицы соединены угловой пружиной, как показано на рис. 1:
где Cs – жесткость, φ – угол образованный 2-мя соседними связями.
Модель[править]
В данной программе в начальный момент времени задаются:
- - отношение жесткости линейной пружины к угловой пружине
- - отношение начального вертикального смещения к равновесной длине пружины (в процентах)
- - отношение скорости правой частицы к
- Возможность придания скорости левой частице
Текст программы на языке JavaScript:
1 window.addEventListener("load", program_code, false);
2 function program_code() {
3 var ctx = canvas_example.getContext("2d");
4 var w = canvas_example.width;
5 var h = canvas_example.height;
6 ctx.strokeRect(0,0,w,h);
7 //var ctx1 = canvas_example1.getContext("2d");
8 //var w1 = canvas_example1.width;
9 //var h1 = canvas_example1.height;
10 //ctx1.strokeRect(0,0,w1,h1);
11
12 var v0 = 10; //Скорость правого шарика
13 var v01 = 0; //Скорость левого шарика
14 var m = 10; //Масса шарика
15 var ht = 20; //параметр рисования
16 var htt = 40; //параметр рисования
17 var Cs = 10000; //Жесткость на изгиб
18 var rad = 5; //Радиус шариков
19 var dt = 0.01;
20 var tt = 0; // Время
21 var dy=document.getElementById('r3'); //Начальные смещения по оси y, задаваемые пользователем
22 var ppp2=document.getElementById('text3');
23 ppp2.innerHTML=dy.value;
24 dy.oninput = function() {
25 ppp2.innerHTML="<"+dy.value;
26 for (var i=0;i<u_len;i++){
27 Yt[i] = dy.value*Math.random()+h/2;
28 }
29 Yt[0] = h/2;
30 Yt[u_len-1] = h/2;
31 r_ = [Xt,Yt];
32 defaultdraw();
33 }
34 var F_ = [0,0];
35 var pp = [0,0];
36 var FF = [];
37 var v = [[v01,0,0,0,0,0,0,0,0,v0],[0,0,0,0,0,0,0,0,0,0]]; //массив скоростей
38 var kk = -5; //Жесткость пружины
39 var Xt = [w/11,2*w/11,3*w/11,4*w/11,5*w/11,6*w/11,7*w/11,8*w/11,9*w/11,10*w/11]; //начальные положения частиц по оси X
40 var u_len = Xt.length;
41 var Yt = []; //Начальные смещения по оси y
42 for (var i=0;i<u_len;i++){
43 Yt[i] = 1*Math.random()+h/2;
44 }
45 Yt[0] = h/2; //Граничные условия
46 Yt[u_len-1] = h/2;
47 var r_ = [Xt,Yt]; //Вектор перемещений
48 var r12_ = [[0,0,0,0,0,0,0,0,0],[0,0,0,0,0,0,0,0,0]]; //Вектор между частицами
49 var r12 = [0,0,0,0,0,0,0,0,0]; //Модуль вектора перемещений
50
51 // Рисование в начальном положении
52 function defaultdraw(){
53 ctx.clearRect(0,0,w,h);
54 ctx.strokeRect(0,0,w,h);
55 for (var i=0;i<u_len;i++){
56 ctx.beginPath();
57 ctx.arc(Xt[i],Yt[i],rad,0,Math.PI*2);
58 ctx.fill();
59 }
60 for (var i=0;i<u_len-1;i++){
61 var x_st = r_[0][i]
62 var y_st = r_[1][i]
63 var x_end = r_[0][i+1]
64 var y_end = r_[1][i+1]
65 var l = r_[0][i+1] - r_[0][i];
66 var ly = r_[1][i+1] - r_[1][i]
67 ctx.beginPath();
68 ctx.bezierCurveTo(x_st, y_st, x_st + l / 4, y_st + ly / 4 + ht, x_st + l / 2, y_st + ly / 2);
69 ctx.bezierCurveTo(x_st + l / 2, y_st + ly / 2, x_st + 3 * l / 4, y_st + 3 * ly / 4 - ht, x_st + l, y_st + ly);
70 ctx.stroke();
71 }
72 for (var i=0;i<u_len-2;i++){
73 var x_st = r_[0][i]
74 var y_st = r_[1][i]
75 var x_end = r_[0][i+1]
76 var y_end = r_[1][i+1]
77 var x_end_end = r_[0][i+1]
78 var y_end_end = r_[1][i+1]
79 var l = r_[0][i+1] - r_[0][i]
80 var ly = r_[1][i+1] - r_[1][i]
81 var l1 = r_[0][i+2] - r_[0][i+1]
82 var ly1 = r_[1][i+2] - r_[1][i+1]
83 ctx.beginPath();
84 ctx.bezierCurveTo(x_st+l/2, y_st+ly/2, x_st + l, y_st+ly+htt , x_st+l + l1/2, y_st +ly+ ly1/2);
85 ctx.stroke();
86 }
87 }
88 defaultdraw();
89
90 var Css=document.getElementById('r1'); //Задаваемая угловая жесткость
91 var ppp=document.getElementById('text');
92 var k1=document.getElementById('r2'); //Задаваемая жесткость
93 var ppp1=document.getElementById('text2');
94 ppp.innerHTML=Css.value;
95 ppp1.innerHTML=-k1.value;
96 Css.oninput = function() {
97 ppp.innerHTML=Css.value;
98 }
99 k1.oninput = function() {
100 ppp1.innerHTML=-k1.value;
101 }
102
103 // Физический модуль
104 function physics() {
105 chbox=document.getElementById('one'); // Будет ли скорость у левой частицы
106 if (chbox.checked) {
107 v01 = v0
108 }
109 else {
110 v01 = 0
111 }
112
113 Cs = Css.value
114 kk = k1.value
115 for (var i=0;i<u_len-1;i++){
116 r12_[0][i] = r_[0][i+1]-r_[0][i];
117 r12_[1][i] = r_[1][i+1]-r_[1][i];
118 }
119 for (var i=0;i<u_len-1;i++){
120 r12[i] = Math.sqrt(r12_[0][i]*r12_[0][i]+r12_[1][i]*r12_[1][i]);
121 }
122 f = []
123 for (var i=0;i<2;i++){
124 f[i] = []
125 for (var j=0;j<u_len;j++){
126 f[i][j] = 0
127 }
128 }
129 for (var i=0;i<u_len-2;i++){
130 F_[0] = kk*((w/(u_len+1))-r12[i])*(r12_[0][i]/r12[i])
131 F_[1] = kk*((w/(u_len+1))-r12[i])*(r12_[1][i]/r12[i])
132
133 etta = -(r12_[0][i]*r12_[0][i+1]+r12_[1][i]*r12_[1][i+1]) / ( r12[i]*r12[i+1] );
134 phi = Math.acos(etta);
135 Fp = [0,0];
136 Fn = [0,0];
137 F = [0,0];
138 if (phi != Math.PI){
139 koef = Cs * (Math.PI - phi)/(Math.sqrt(1-etta*etta) * r12[i] * r12[i+1]);
140 A = [[ 1 - Math.pow(r12_[0][i]/r12[i],2), -r12_[0][i]*r12_[1][i]/(r12[i]*r12[i])], [-r12_[0][i]*r12_[1][i]/(r12[i]*r12[i]), 1 - Math.pow(r12_[1][i]/r12[i],2) ]];
141 B = [[ 1 - Math.pow(r12_[0][i+1]/r12[i+1],2), -r12_[0][i+1]*r12_[1][i+1]/(r12[i+1]*r12[i+1])],[ -r12_[0][i+1]*r12_[1][i+1]/(r12[i+1]*r12[i+1]), 1 - Math.pow(r12_[1][i+1]/r12[i+1],2) ]];
142 Fp = [-koef*(r12_[0][i+1]*A[0][0]+r12_[1][i+1]*A[1][0]),-koef*(r12_[0][i+1]*A[0][1]+r12_[1][i+1]*A[1][1])];
143 Fn = [koef*(r12_[0][i]*B[0][0]+r12_[1][i]*B[1][0]),koef*(r12_[0][i]*B[0][1]+r12_[1][i]*B[1][1])];
144 F = [-Fn[0] - Fp[0],-Fn[1] - Fp[1]];
145 }
146 f[0][i] = f[0][i] + F_[0] + Fp[0];
147 f[1][i] = f[1][i] + F_[1] + Fp[1];
148 f[0][i+1] = f[0][i+1]-F_[0]+F[0];
149 f[1][i+1] = f[1][i+1]-F_[1]+F[1];
150 f[0][i+2] = f[0][i+2]+Fn[0];
151 f[1][i+2] = f[1][i+2]+Fn[1];
152 }
153 pp[0] = kk*((w/(u_len+1))-r12[u_len-2])*(r12_[0][u_len-2]/r12[u_len-2])
154 pp[1] = kk*((w/(u_len+1))-r12[u_len-2])*(r12_[1][u_len-2]/r12[u_len-2])
155 f[0][u_len-2] = f[0][u_len-2] +pp[0];
156 f[1][u_len-2] = f[1][u_len-2] +pp[1];
157 f[0][u_len-1] = f[0][u_len-1]-pp[0];
158 f[1][u_len-1] = f[1][u_len-1]-pp[1];
159 for (var i=0;i<u_len-1;i++){
160 v[0][i] = v[0][i] + (f[0][i]/m) * dt;
161 v[1][i] = v[1][i] + (f[1][i]/m) * dt;
162 }
163
164
165 v[0][0] = v01;
166 v[1][0] = 0;
167 v[0][u_len-1] = -v0;
168 v[1][u_len-1] = 0;
169 for (var i=0;i<u_len;i++){
170 r_[0][i] = r_[0][i] + v[0][i] * dt;
171 r_[1][i] = r_[1][i] + v[1][i] * dt;
172 }
173 }
174 //Модуль рисования
175 function draw() {
176 tt=tt+1
177 // Условия остановки выполнения программы
178 if ((tt>6300) && (v01==0)){
179 clearInterval(tim)
180 }
181 if ((tt>3150) && (v01!=0)){
182 clearInterval(tim)
183 }
184 ctx.clearRect(0,0,w,h);
185 ctx.strokeRect(0,0,w,h);
186 // Рисование шариков
187 for (var i=0;i<u_len;i++){
188 ctx.beginPath();
189 ctx.arc(r_[0][i],r_[1][i],rad,0,Math.PI*2);
190 ctx.fill();
191 }
192 //if ((tt%10==0){
193 FF.push(f[0][u_len-1])
194 //}
195 if (tt==60){
196 console.log(JSON.stringify(FF))
197 }
198 // График силы
199 //for (var i=0;i<u_len;i++){
200 // ctx1.beginPath();
201 // ctx1.arc(tt/10,-f[0][u_len-1]/10+h/2,1,0,Math.PI*2);
202 // ctx1.stroke();
203 //}
204 ctx.beginPath();
205 for (var i=0;i<u_len-1;i++){
206 var x_st = r_[0][i]
207 var y_st = r_[1][i]
208 var x_end = r_[0][i+1]
209 var y_end = r_[1][i+1]
210 var l = r_[0][i+1] - r_[0][i];
211 var ly = r_[1][i+1] - r_[1][i]
212 ctx.beginPath();
213 ctx.bezierCurveTo(x_st, y_st, x_st + l / 4, y_st + ly / 4 + ht, x_st + l / 2, y_st + ly / 2);
214 ctx.bezierCurveTo(x_st + l / 2, y_st + ly / 2, x_st + 3 * l / 4, y_st + 3 * ly / 4 - ht, x_st + l, y_st + ly);
215 ctx.stroke();
216 }
217 for (var i=0;i<u_len-2;i++){
218 var x_st = r_[0][i]
219 var y_st = r_[1][i]
220 var x_end = r_[0][i+1]
221 var y_end = r_[1][i+1]
222 var x_end_end = r_[0][i+1]
223 var y_end_end = r_[1][i+1]
224 var l = r_[0][i+1] - r_[0][i]
225 var ly = r_[1][i+1] - r_[1][i]
226 var l1 = r_[0][i+2] - r_[0][i+1]
227 var ly1 = r_[1][i+2] - r_[1][i+1]
228 ctx.beginPath();
229 ctx.bezierCurveTo(x_st+l/2, y_st+ly/2, x_st + l, y_st+ly+htt , x_st+l + l1/2, y_st +ly+ ly1/2);
230 ctx.stroke();
231 }
232 ctx.closePath();
233 }
234 // Контрольный модуль
235 function control(){
236 physics();
237 draw();
238 }
239 var tim;
240 // Функция остановки программы
241 function go1(){
242 clearInterval(tim);
243 }
244 // Функция работы программы
245 function go(){
246 clearInterval(tim);
247 control() ;
248 tim = setInterval(control,1000/60);
249 }
250 button_aler.onclick=go //Кнопка старта
251 button_aler1.onclick=go1 //Кнопка остановки
252 }
Результаты моделирования[править]
Графики зависимости обезрамеренной продольной силы , где - Эйлерова критическая сила в статике, от времени (от количества итераций) при различных значениях параметров построены в python по данным полученным из программы javascript.
- Как видно из графиков зависимости обезрамеренной продольной силы от времени (от количества итераций) (Рис. 2 и Рис. 3) линейный участок роста продольной силы имеет наибольшую длину при малых начальных вертикальных смещениях. Следовательно критическая сила, при которой продольная сила перестает расти линейно и начинает уменьшаться, наступает для начального вертикального смещения ""относительно равновесной длины пружины при большей силе, нежели при начальном смещении "" или ""относительно равновесной длины пружины .
- Из графиков зависимости обезрамеренной продольной силы от времени (от количества итераций) (Рис. 4, Рис. 5 и Рис. 6) видно, что линейный участок роста продольной силы имеет наибольшую длину при большом значении скорости правой частицы. Это справедливо для любого начального вертикального смещения частиц. Следовательно критическая сила, при которой продольная сила перестает расти линейно и начинает уменьшаться, наступает для скорости правой частицы при большей силе, нежели при скорости правой частицы или .
Ссылки[править]
- Kuzkin V.A., Dannert M.M.: Dynamic buckling of a column under constant speed compression. Acta Mech (2016) 227:1645-1652.