Участник:Isi1313188 — различия между версиями
(→Расчеты элементов проекта) |
(→Расчёты элементов проекта) |
||
| (не показано 128 промежуточных версий этого же участника) | |||
| Строка 25: | Строка 25: | ||
* Вишнев Артем | * Вишнев Артем | ||
* Данилова Дарья | * Данилова Дарья | ||
| + | * Доенина Анна | ||
* Егунова Анастасия | * Егунова Анастасия | ||
* Ефимов Евгений | * Ефимов Евгений | ||
| Строка 38: | Строка 39: | ||
==Работа по проекту== | ==Работа по проекту== | ||
===Действия, выполняемые машиной Голдберга=== | ===Действия, выполняемые машиной Голдберга=== | ||
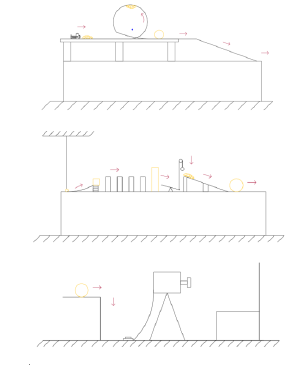
| − | [[File: | + | [[File:22Snimok.png|thumb|Схема устройства этапов Машины Голдберга, совершающей фотоснимок]] |
# Запуск резинки, толкающей машинку | # Запуск резинки, толкающей машинку | ||
# Машинка совершает элемент "мертвая петля" на трассе | # Машинка совершает элемент "мертвая петля" на трассе | ||
| Строка 45: | Строка 46: | ||
# Маятник толкает домино | # Маятник толкает домино | ||
# В процессе падают все доминошки | # В процессе падают все доминошки | ||
| − | # Последняя из домино толкает | + | # Последняя из домино толкает брусок |
| − | # | + | # Брусок толкает машинку |
# Машинка толкает кубик | # Машинка толкает кубик | ||
# Кубик падает на рычаг | # Кубик падает на рычаг | ||
| Строка 73: | Строка 74: | ||
===Инструменты для создания проекта=== | ===Инструменты для создания проекта=== | ||
| − | + | * Лобзик электрический | |
| + | * Напильник ручной | ||
| + | * Шуруповерт | ||
| + | * Клеевой пистолет | ||
| + | * Молоток | ||
===Этапы создания проекта=== | ===Этапы создания проекта=== | ||
| Строка 99: | Строка 104: | ||
|- | |- | ||
| 15.04.19 | | 15.04.19 | ||
| − | | | + | | Окончательное создание первых этапов установки и контроль их работы |
| − | | | + | | Неполная работоспособность установки, в следствие чего возникла необходимость замены некоторых материалов |
| − | | | + | | Первые этапы установки находятся в рабочем состояние примерно на 75% |
|- | |- | ||
| 16.04.19 | | 16.04.19 | ||
| − | | | + | | Сбор отдельных этапов установки, требующих наиболее прикладную составляющую, и проверка их на работоспособность, примерный расчёт необходимых параметром для этих этапов |
| − | | | + | | Нехватка материалов, поэтому необходимость докупать материалы; появление необходимости получения навыков работы с прикладными инструментами |
| − | | | + | | Первые этапы установки готовы и работают в идеальном состоянии, частично созданы последующие этапы машины |
|- | |- | ||
| 29.04.19 | | 29.04.19 | ||
| − | | | + | | Сбор всех этапов установки в единое целое, проверка их работоспособности |
| − | | | + | | Наличие недочетов в работе установки |
| − | | | + | | Установка практически приобрела свой окончательный вид |
|- | |- | ||
| 30.04.19 | | 30.04.19 | ||
| − | | | + | | Повторный, полный сбор установки с устранением выявленных неполадок |
| − | | | + | | Практически не возникло, были убраны небольшие недочеты, чтобы установка работала каждый раз в штатном режиме |
| − | | | + | | Окончательно готовая установка |
|- | |- | ||
| 14.05.19 | | 14.05.19 | ||
| − | | | + | | Проведение контрольных запусков машины, оформление вики-страницы |
| − | + | | Трудности при создание вики-страницы из-за не знания языка программирования | |
| − | + | | Удачное прохождение машиной всех этапов, создание фотографий посредством её; приобретение необходимые знаний по оформлению вики-страницы, преодоление трудностей | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | == | + | ==Расчёты элементов проекта== |
| − | * | + | *Расчёт скорости машины, с которой она поедет при запуске пружины (Войтенко М.) |
<div class="mw-collapsible mw-collapsed"> | <div class="mw-collapsible mw-collapsed"> | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| − | |||
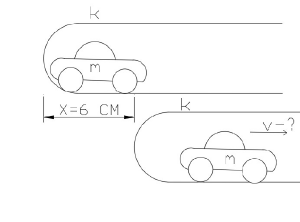
::<math>Дано:</math> | ::<math>Дано:</math> | ||
| + | [[File:Схема для расчета скорости машины.png|thumb|Схема для расчета скорости машины, с которой она поедет при запуске пружины]] | ||
::<math>k=0{,}1~кН/м</math> | ::<math>k=0{,}1~кН/м</math> | ||
::<math>m=40~г</math> | ::<math>m=40~г</math> | ||
| Строка 168: | Строка 143: | ||
::<math>Решение:</math> | ::<math>Решение:</math> | ||
| − | ::<math>Согласно ~закону ~сохранения ~энергии ~при ~отсутствии ~неконсервативных ~сил | + | ::<math>Согласно ~закону ~сохранения ~энергии ~при ~отсутствии ~неконсервативных~сил</math> |
| + | ::<math>полная ~механическая ~энергия ~системы ~тел ~сохраняется.</math> | ||
::<math>E=const E _{1}=E _{2}</math> | ::<math>E=const E _{1}=E _{2}</math> | ||
| − | ::<math>Конечная ~энергия ~системы ~определяется ~только ~кинетической ~энергией ~машинки, | + | ::<math>Конечная ~энергия ~системы ~определяется ~только ~кинетической ~энергией~машинки,</math> |
| + | ::<math>которая ~определяется ~по ~формуле:</math> | ||
::<math>E _{2}=\frac{(m\cdot v^2)}{2}</math> | ::<math>E _{2}=\frac{(m\cdot v^2)}{2}</math> | ||
| − | ::<math>Начальная ~энергия ~системы ~определяется~потенциальной ~энергией ~растянутой ~резинки:</math> | + | ::<math>Начальная ~энергия ~системы ~определяется~потенциальной ~энергией</math> |
| + | ::<math>~растянутой ~резинки:</math> | ||
::<math>E _{1} = \frac{(k\cdot x^2)}{2} </math> | ::<math>E _{1} = \frac{(k\cdot x^2)}{2} </math> | ||
::<math>В ~итоге:</math> | ::<math>В ~итоге:</math> | ||
| Строка 179: | Строка 157: | ||
::<math>v\approx3~м/c </math> | ::<math>v\approx3~м/c </math> | ||
| − | ::<math>Ответ: | + | ::<math>Ответ:v\approx3~м/c. </math> |
| − | |||
</div> | </div> | ||
</div> | </div> | ||
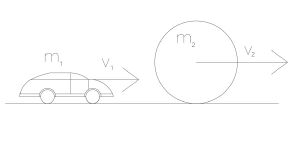
| − | + | *Расчёт скорости машинки при соударении с шариком (Егунова А.) | |
| − | * | ||
<div class="mw-collapsible mw-collapsed"> | <div class="mw-collapsible mw-collapsed"> | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| Строка 211: | Строка 187: | ||
::<math>Выразим ~v_{1} ~через ~ускорение:</math> | ::<math>Выразим ~v_{1} ~через ~ускорение:</math> | ||
::<math> a_{1}=\frac{dv_{1}}{dt} </math> | ::<math> a_{1}=\frac{dv_{1}}{dt} </math> | ||
| − | ::<math> a_{1} \cdot | + | ::<math> a_{1} \cdot \int\limits_{0}^{t_{1}} \, dt = \int\limits_{v_{0}}^{v_{1}} \, dv </math> |
::<math> a_{1}=\frac{v_{1}-v_{0}}{t_{1}} </math> | ::<math> a_{1}=\frac{v_{1}-v_{0}}{t_{1}} </math> | ||
::<math> v_{1}=a_{1} \cdot t_{1}+v_{0}</math> | ::<math> v_{1}=a_{1} \cdot t_{1}+v_{0}</math> | ||
| Строка 234: | Строка 210: | ||
::<math> v_{3}=-1{,}792 \cdot 0{,}125+1{,}128=0{,}904 ~м/с</math> | ::<math> v_{3}=-1{,}792 \cdot 0{,}125+1{,}128=0{,}904 ~м/с</math> | ||
| − | ::<math>Ответ: | + | ::<math>Ответ:v_{3}=0{,}904~м/с.</math> |
| − | |||
</div> | </div> | ||
</div> | </div> | ||
| − | + | *Расчёт скорости мяча, приобретенной в результате упругого соударения с машиной (Доенина А.) | |
| − | |||
| − | * | ||
<div class="mw-collapsible mw-collapsed"> | <div class="mw-collapsible mw-collapsed"> | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
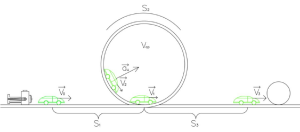
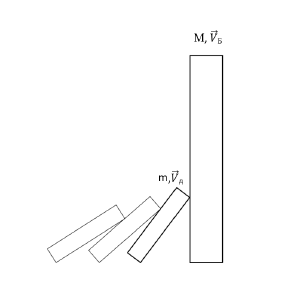
| − | [[File: | + | [[File:Схема для расчёта скорости мяча.jpg|thumb|Схема для расчёта приобретенной в результате упругого соударения с машиной скорости мяча |
| + | ]] | ||
::<math>Дано:</math> | ::<math>Дано:</math> | ||
::<math>m_{1}=0{,}04~кг</math> | ::<math>m_{1}=0{,}04~кг</math> | ||
::<math>m_{2}=0{,}056~кг</math> | ::<math>m_{2}=0{,}056~кг</math> | ||
| − | ::<math> | + | ::<math>v_{1}=0{,}904~м/с</math> |
| − | ::<math>Найти:~ | + | ::<math>Найти:~v_{2}</math> |
::<math>Решение:</math> | ::<math>Решение:</math> | ||
| Строка 257: | Строка 231: | ||
::<math>p_{11}+p_{12}=p_{21}+p_{22} </math> | ::<math>p_{11}+p_{12}=p_{21}+p_{22} </math> | ||
::<math>p_{12}=0,~так~как~мяч~в~начале~покоится,~а~p_{21}=0,~так~как~машина~останавливается.~Следовательно: </math> | ::<math>p_{12}=0,~так~как~мяч~в~начале~покоится,~а~p_{21}=0,~так~как~машина~останавливается.~Следовательно: </math> | ||
| − | ::<math>m_{1} \cdot | + | ::<math>m_{1} \cdot v_{1}=m_{2} \cdot v_{2} </math> |
::<math>Выражаем~скорость~шарика:</math> | ::<math>Выражаем~скорость~шарика:</math> | ||
| − | ::<math> | + | ::<math>v_{2}=\frac{m_{1} \cdot v_{1}}{m_{2}} </math> |
| − | ::<math> | + | ::<math>Подставим~численные~значения: </math> |
| + | ::<math>v_{2}=\frac{0{,}04~кг \cdot 0{,}904~м/c}{0{,}056~кг} </math> | ||
| + | ::<math>v_{2}=0{,}65~м/с </math> | ||
| − | ::<math>Ответ: | + | ::<math>Ответ:0{,}65~м/с </math> |
| − | |||
</div> | </div> | ||
</div> | </div> | ||
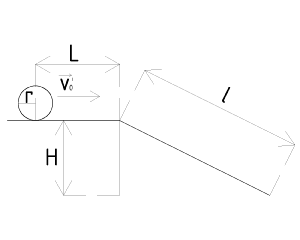
| + | *Расчёт скорости шара в конце наклонной плоскости (Ефимов Е.) | ||
| + | <div class="mw-collapsible mw-collapsed"> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | [[File:4задача.png|thumb|Расчет скорости шара в конце наклонной плоскости]] | ||
| + | ::<math>Дано:</math> | ||
| + | ::<math>L=15~см</math> | ||
| + | ::<math>H=13{,}3~см</math> | ||
| + | ::<math>l=29{,}8~см</math> | ||
| + | ::<math>r=3{,}1~см</math> | ||
| + | ::<math>v_{0}'=0{,}65~м/c</math> | ||
| − | + | ::<math>Найти:~v</math> | |
| + | |||
| + | ::<math>Решение:</math> | ||
| + | ::<math>Для~решения~задачи~используем~формулу~(1):</math> | ||
| + | ::<math>v=\omega \cdot r~(1)</math> | ||
| + | ::<math>где~\omega=\beta \cdot t</math> | ||
| + | ::<math>\beta=\frac{M}{l}</math> | ||
| + | ::<math>Найдем~момент~внешних~сил~относительно~точки~касания~плоскости~и~шара.</math> | ||
| + | ::<math>Этот~момент~будет~обеспечиваться~только~силой~тяжести,~т.к.~остальные~моменты~будут~равны~0.</math> | ||
| + | ::<math>M=m \cdot g \cdot r \cdot sin\alpha</math> | ||
| + | ::<math>Найдем~I~(момент~инерции~шара~относительно~оси,~проходящей~через~точку~касания~плоскости)~при~помощи~теоремы~Штейнера:</math> | ||
| + | ::<math>I=I_{ц}+m \cdot r^2</math> | ||
| + | ::<math>Момент~инерции~относительно~центра~шара~вычисляется~следующим~образом:</math> | ||
| + | ::<math>I_{ц}=\frac{2}{5} \cdot m \cdot r^2</math> | ||
| + | ::<math>Таким~образом:</math> | ||
| + | ::<math>I=\frac{7}{5} \cdot m \cdot r^2</math> | ||
| + | ::<math>Подставив~полученные~выражения~в~формулу~(1),~получим:</math> | ||
| + | ::<math>v=\frac{5}{7} \cdot g \cdot t \cdot sin\alpha~(2)</math> | ||
| + | ::<math>Используя~формулы~(3)~и~(4),~выразим~время~(5):</math> | ||
| + | ::<math>S=\frac{v^2-v_{0}^2}{2 \cdot a}~(3)</math> | ||
| + | ::<math>a=\frac{v^2-v_{0}^2}{2 \cdot S}</math> | ||
| + | ::<math>v=v_{0}+a \cdot t~(4)</math> | ||
| + | ::<math>v=v_{0}+\frac{v^2-v_{0}^2}{2 \cdot S} \cdot t~(4)</math> | ||
| + | ::<math>t=\frac{2S}{v+v_{0}}~(5)</math> | ||
| + | ::<math>Подставим~(5)~в~(2):</math> | ||
| + | ::<math>v=\frac{5}{7} \cdot g \cdot \frac{2S}{v+v_{0}} \cdot sin\alpha~</math> | ||
| + | ::<math>v^2+v \cdot v_{0}-\frac{10}{7} \cdot g \cdot l \cdot \frac{H}{l}=0~(6)</math> | ||
| + | ::<math>Так~как~силой~трения~качения~в~условиях~данной~задачи~мы~пренебрегаем,~то~в~качестве</math> | ||
| + | ::<math>𝑣_{0}~мы~принимаем~v_{0}~-~скорость,~которую~сообщает~шару~машинка~в~предыдущей~задаче.</math> | ||
| + | ::<math>Подставим~численные~значения~в~формулу~(6):</math> | ||
| + | ::<math>700 \cdot v^2+455 \cdot v -1329{,}08=0</math> | ||
| + | ::<math>Решим~квадратное~уравнение,~получим~два~корня:</math> | ||
| + | ::<math>v_{1}=1{,}091~м/c</math> | ||
| + | ::<math>v_{2}=-1{,}741~м/c</math> | ||
| + | ::<math>Отрицательное~v~не~подходит~нам,~так~как~нас~интересует~модуль~скорости.</math> | ||
| + | ::<math>Поэтому~ответом~данной~задачи~является~v=1{,}091~м/c</math> | ||
| + | |||
| + | ::<math>Ответ:v=1{,}091~м/с</math> | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
| + | |||
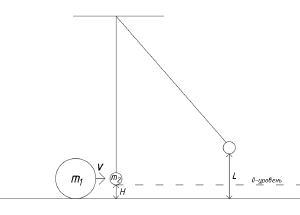
| + | *Расчёт оптимальной массы шарика, необходимой для поднятия после удара на высоту h (Лось П.) | ||
<div class="mw-collapsible mw-collapsed"> | <div class="mw-collapsible mw-collapsed"> | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| − | [[File: | + | [[File:2019-05-28 16-51-17.png|thumb|Расчет оптимальной массы шарика, необходимой для поднятия после удара на высоту h]] |
::<math>Дано:</math> | ::<math>Дано:</math> | ||
| − | ::<math>m_{ | + | ::<math>m_{1}=0{,}056~кг</math> |
| − | ::<math>m_{ | + | ::<math>v=1{,}091~м/с</math> |
| − | ::<math> | + | ::<math>H=0{,}04~м</math> |
| + | ::<math>L=0{,}12~м</math> | ||
| + | ::<math>g=9{,}8~м/с^2</math> | ||
| + | |||
| + | ::<math>Найти:~m_{2}</math> | ||
| + | |||
| + | ::<math>Решение:</math> | ||
| + | ::<math>Шарик~массы~m_{2},~подвешенный~на~нити,~находится~на~некоторой~высоте~h,</math> | ||
| + | ::<math>которая~равна~L-H=0{,}12~м-0{,}04~м=0{,}08~м</math> | ||
| + | ::<math>На~него~налетает~мяч~массы~m_{1},~происходит~упругое ~соударение,</math> | ||
| + | ::<math>поэтому~запишем~закон~сохранения~импульса~(ЗСИ):</math> | ||
| + | ::<math>m_{1} \cdot v=m_{2} \cdot v',~где~v'-скорость~шарика~после~соударения.</math> | ||
| + | ::<math>v'=\frac{m_{1} \cdot v}{m_{2}}</math> | ||
| + | ::<math>Запишем~также~закон~сохранения~энергии(ЗСЭ)~для~шарика,~учитывая,~что~он~поднимется~на~высоту~h:</math> | ||
| + | ::<math>\frac{m_{2} \cdot v'^2}{2}=m_{2} \cdot g \cdot h</math> | ||
| + | ::<math>Подставив~v',~получим:</math> | ||
| + | ::<math>\frac{m_{2} \cdot m_{1}^2 \cdot v^2}{2 \cdot m_{2}^2}=m_{2} \cdot g \cdot h</math> | ||
| + | ::<math>Выразим~m_{2}:</math> | ||
| + | ::<math>m_{2}=\frac{m_{1} \cdot v}{\sqrt{2 \cdot g \cdot h}}</math> | ||
| + | ::<math>m_{2}=\frac{0{,}056~кг \cdot 1{,}091~м/с}{\sqrt{2 \cdot 9{,}8~м/с^2 \cdot 0{,}08~м}}=0{,}04~кг</math> | ||
| + | ::<math>Сравниваем ~с ~экспериментальным ~значением ~массы~и~видим,~что ~масса ~получилась ~подходящей</math> | ||
| − | ::<math>Найти:~ | + | ::<math>Ответ:m _{2}=0{,}04~кг.</math> |
| + | |||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | *Расчёт оптимальной высоты подъема шарика (Панова Ю.) | ||
| + | <div class="mw-collapsible mw-collapsed"> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | [[File:6 zadachka.png|thumb|Расчет оптимальной высоты подъема шарика]] | ||
| + | ::<math>Дано:</math> | ||
| + | ::<math>v=1{,}2~м/с</math> | ||
| + | ::<math>g=9{,}8~м/с^2</math> | ||
| + | |||
| + | ::<math>Найти:~h</math> | ||
::<math>Решение:</math> | ::<math>Решение:</math> | ||
| − | ::<math> | + | ::<math>Используем~закон~сохранения~энергии~(ЗСЭ)</math> |
| − | ::<math> | + | ::<math>E_{к}=E_{п}</math> |
| − | ::<math> | + | ::<math>\frac{m \cdot v^2}{2}=m \cdot g \cdot h</math> |
| − | ::<math> | + | ::<math>Получаем~значение~оптимальной~высоты~h:</math> |
| − | + | ::<math>h=\frac {v^2}{2g}=\frac {1{,}2^2}{2 \cdot 9{,}8}=0{,}07~м</math> | |
| − | ::<math> | + | ::<math>Сравниваем~с~экспериментальным~значением~высоты,~которое~равно~0{,}064~м</math> |
| − | ::<math>Ответ: | + | ::<math>Ответ:h=0{,}07~м</math> |
| − | |||
</div> | </div> | ||
</div> | </div> | ||
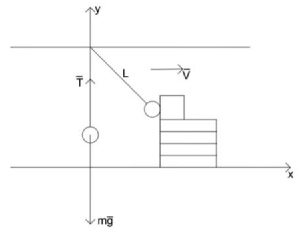
| + | *Расчёт скорости кубика, приобретённой в результате cоударения с шариком на нити (Вишнев А.) | ||
| + | <div class="mw-collapsible mw-collapsed"> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | [[File:Задача77.png|thumb|Расчет скорости кубика, приобретенной в результате соударения с шариком на нити]] | ||
| + | ::<math>Дано:</math> | ||
| + | ::<math>m=0{,}009~кг</math> | ||
| + | ::<math>M=0{,}016~кг</math> | ||
| + | ::<math>g=9{,}8~м/c^2</math> | ||
| + | ::<math>\left | \vec{T} \right |=0{,}2~Н</math> | ||
| + | ::<math>L=0{,}2~м</math> | ||
| + | |||
| + | ::<math>Найти:~v_{кубик}</math> | ||
| + | |||
| + | ::<math>Решение:</math> | ||
| + | ::<math>Обозначим~массу~шарика~через~m,~а~массу~кубика~через~M. </math> | ||
| + | ::<math>По~второму~закону~Ньютона~в~проекциях~на~ось~Oy~инерциальной~системы~отсчёта~Oxy: </math> | ||
| + | ::<math>\frac{m \cdot v_{шарик}^2}{L}=T-m \cdot g</math> | ||
| + | ::<math>Следовательно:</math> | ||
| + | ::<math>v_{шарик}=\sqrt{(\frac{T}{m}-g) \cdot L}</math> | ||
| + | ::<math>Происходит~упругое~соударение.~По~закону~сохранения~импульса~(ЗСИ):</math> | ||
| + | ::<math>m \cdot v_{шарик}=M \cdot v_{кубик} </math> | ||
| + | ::<math>Соответственно~скорость~кубика~равна:</math> | ||
| + | ::<math>v_{кубик}=\frac{m \cdot v_{шарик}}{M}=\frac{m \cdot \sqrt{(\frac{T}{m}-g) \cdot L}}{M}</math> | ||
| + | ::<math>Получим~численное~значение:</math> | ||
| + | ::<math>v_{кубик}=\frac{0{,}009~кг \cdot \sqrt{(\frac{0{,}2~Н}{0{,}009~кг}-9{,}8~Н) \cdot 0{,}2~м}}{0{,}016~кг}\approx 1{,}2~м/c</math> | ||
| + | |||
| + | ::<math>Ответ:v_{кубик}=1{,}2~м/c</math> | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
| − | * | + | *Расчёт скорости домино (Савчиков А.) |
<div class="mw-collapsible mw-collapsed"> | <div class="mw-collapsible mw-collapsed"> | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
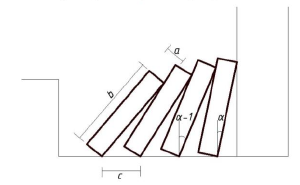
| − | ::<math> | + | [[File:Zadacha 8 1.png|thumb|Расчет скорости домино]] |
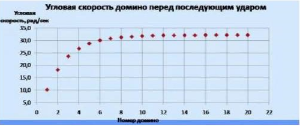
| − | ::<math> | + | [[File:Zadacha 8 2.png|thumb|Угловая скорость домино перед последующим ударом]] |
| − | ::<math> | + | ::<math>Дано:</math> |
| + | ::<math>a=15~мм</math> | ||
| + | ::<math>b=75~мм</math> | ||
| + | ::<math>c=30~мм</math> | ||
| + | ::<math>M=16~г</math> | ||
| + | ::<math>m=17~г</math> | ||
| + | ::<math>v_{кубик}=1{,}2~м/c</math> | ||
| + | |||
| + | ::<math>Найти:~cоотношение~скоростей~домино~и~скорость~последнего~домино</math> | ||
| + | |||
| + | ::<math>Решение:</math> | ||
| + | ::<math>Для~нахождения~нужных~нам~величин~условимся~считать,</math> | ||
| + | ::<math>что~все~домино~являются~однородными~гладкими~прямоугольными~брусками.</math> | ||
| + | ::<math>Все~домино~в~начальный~момент~стоят~на~ровной~горизонтальной~плоскости.</math> | ||
| + | ::<math>Во~время~движения~трение~между~домино~отсутствует.</math> | ||
| + | ::<math>Проскальзывания~домино~на~поверхности~нет.</math> | ||
| + | ::<math>Тогда~для~каждой~пары~соседних~домино~выполняется~равенство:</math> | ||
| + | ::<math>sin((\alpha-1)-\alpha)=\frac{c \cdot cos\alpha}{b}-\frac{a}{b}</math> | ||
| + | ::<math>Пользуясь~этим~соотношением~можно~вычислить~углы~наклона~каждого~домино~перед~N.</math> | ||
| + | ::<math>Дифференцируя~данное~равенство,~можно~найти~соотношение~скоростей~этих~домино~в~каждый~момент~времени:</math> | ||
| + | ::<math>(\alpha-1)'=(1-\frac{c \cdot sin\alpha}{b \cdot cos((\alpha-1)-\alpha)}) \cdot \alpha'</math> | ||
| + | ::<math>В~~процессе~каждое~домино~ударяет~последующее,~сообщая~ему~некоторую~начальную~скорость.</math> | ||
| + | ::<math>При~этом~согласно~эксперименту~скорость~движения~“волны”~падающих~домино~достигает~своей~постоянной~скорости~примерно~на~10~домино.</math> | ||
| + | ::<math>Поэтому~мы~можем~использовать~данное~равенство~для~нахождения~соотношения~скоростей,~так~как~в~нашем~случае~у~нас~всего~4~элемента.</math> | ||
| + | ::<math>\frac{(\alpha-1)'}{\alpha'}=1-\frac{0{,}03~м \cdot \frac{15}{75}}{0{,}075~м \cdot 0{,}97979}=0{,}9182</math> | ||
| + | ::<math>То~есть~каждая~следующая~домино~(до~10~домино)~будет~иметь~скорость,~в~\frac{1}{0{,}9182}=1{,}089~раз~большую~предыдущей.</math> | ||
| + | ::<math>Согласно~закону~сохранения~импульса(ЗСИ):</math> | ||
| + | ::<math>M \cdot v_{кубик}=m \cdot v_{1} </math> | ||
| + | ::<math>v_{1}=\frac{0{,}016~кг \cdot 1{,}2~м/c}{0{,}017~кг}=1{,}13~м/c</math> | ||
| + | ::<math>v_{4}=1{,}13~м/c \cdot (1{,}089)^3=1{,}45~м/с</math> | ||
| − | ::<math>Ответ: | + | ::<math>Ответ:Соотношение~скоростей~домино~=~1{,}089.~Скорость~последнего~домино~=~1{,}45~м/c</math> |
| − | |||
</div> | </div> | ||
| + | </div> | ||
| + | |||
| + | *Расчёт скорости бруска, приобретенной в результате соударения (Нахимовский А.) | ||
| + | <div class="mw-collapsible mw-collapsed"> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | [[File:1Snimok.png|thumb|Расчет скорости бруска, приобретенной в результате соударения]] | ||
| + | ::<math>Дано:</math> | ||
| + | ::<math>v_{домино}=1{,}45~м/с</math> | ||
| + | ::<math>m_{домино}=0{,}017~кг</math> | ||
| + | ::<math>M_{брусок}=0{,}106~кг</math> | ||
| + | |||
| + | ::<math>Найти:~v_{брусок}</math> | ||
| + | |||
| + | ::<math>Решение:</math> | ||
| + | |||
| + | ::<math>Происходит~соударение~домино,~обладающего~начальной~скоростью,~с~неподвижным~бруском</math> | ||
| + | ::<math>который~впоследствии~начинает~падать.</math> | ||
| + | ::<math>Воспользуемся~законом~сохранения~импульса~(ЗСИ):</math> | ||
| + | ::<math>m_{домино} \cdot v_{домино}=M_{брусок} \cdot v_{брусок} </math> | ||
| + | ::<math>v_{брусок}=\frac{m_{домино} \cdot v_{домино}}{M_{брусок}} </math> | ||
| + | ::<math>Подставим~численные~значения:</math> | ||
| + | ::<math>v_{брусок}=\frac{0{,}017~кг \cdot 1{,}45~м/c}{0{,}106~кг} </math> | ||
| + | ::<math>v_{брусок}=0{,}23~м/c </math> | ||
| + | |||
| + | ::<math>Ответ:v_{брусок}=0{,}23 м/c</math> | ||
| + | |||
| + | |||
| + | ::<math>Примечание:</math> | ||
| + | ::<math>В~данной~задаче~рассматривались~идеальные~условия,~позволяющие~приближённо~рассчитать~искомую~величину.~В~реальности~при~</math> | ||
| + | ::<math>соударении~часть~механической~энергии~будет~переходить~во~внутреннюю~энергию~домино~и~бруска.~Величина,~способная~</math> | ||
| + | ::<math>охарактеризовать~данные~потери,~называется~ударной~вязкостью.</math> | ||
| + | ::<math>Ударная~вязкость~—~способность~материала~поглощать~механическую~энергию~в~процессе~деформации~и~разрушения~под~действием~</math> | ||
| + | ::<math>ударной~нагрузки.</math> | ||
| + | ::<math>В~условиях~нашей~задачи~ударная~вязкость~древесины~была~настолько~мала,~что~её~влиянием~можно~было~пренебречь~и~</math> | ||
| + | ::<math>воспользоваться~законом~сохранения~импульса.</math> | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | *Расчёт ускорения, с которым груз, перекинутый через неподвижный блок, падает на машину (Сиротина А.) | ||
| + | <div class="mw-collapsible mw-collapsed"> | ||
| + | <div class="mw-collapsible-content"> | ||
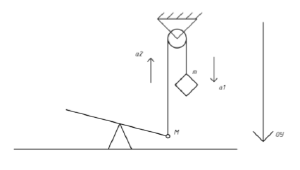
| + | [[File:Zadacha 10 Ot Nasti.png|thumb|Расчет ускорения, с которым груз, перекинутый через неподвижный блок, падает на машину]] | ||
| + | ::<math>Дано:</math> | ||
| + | ::<math>M=0{,}054~кг</math> | ||
| + | ::<math>m=0{,}06~кг</math> | ||
| + | ::<math>g=9{,}81~м/c^2</math> | ||
| + | |||
| + | ::<math>Найти:~a</math> | ||
| + | |||
| + | ::<math>Решение:</math> | ||
| + | ::<math>По~второму~закону~Ньютона~распишем~действующие~на~грузы~силы~и~ускорение,~спроецированные~на~Oy:</math> | ||
| + | ::<math>m \cdot a_{1}=m \cdot g -T_{1}</math> | ||
| + | ::<math>-M \cdot a_{2}=M \cdot g -T_{2}</math> | ||
| + | ::<math>Нить,~перекинутая~через~блок,~нерастяжимая,~значит,~за~одно~и~то~же~время~тела~будут~проходить~одинаковые~пути.</math> | ||
| + | ::<math>Ускорения~будут~постоянны:~a_{1}=a_{2}=a.</math> | ||
| + | ::<math>Кроме~того,~масса~нити~и~блока~пренебрежимо~малы,~в~задаче~не~учитывается~момент~инерции~и~cилы~последнего.</math> | ||
| + | ::<math>Из~этого~следует,~что~сила~натяжения~нити~при~переходе~через~блок~меняет~своё~направление,~но~не~меняет~значение:</math> | ||
| + | ::<math>T_{1}=T_{2}=T</math> | ||
| + | ::<math>m \cdot a_{1}=m \cdot g -T</math> | ||
| + | ::<math>M \cdot a_{2}=T- M \cdot g</math> | ||
| + | ::<math>Решим~систему~уравнений~и~выведем~формулу~нахождения~ускорения~второго~груза:</math> | ||
| + | ::<math>T=m \cdot g - m \cdot a </math> | ||
| + | ::<math>T=M \cdot g + M \cdot a</math> | ||
| + | ::<math>m \cdot g - m \cdot a=M \cdot g + M \cdot a</math> | ||
| + | ::<math>a=\frac{m-M}{m+M} \cdot g</math> | ||
| + | ::<math>Подставив~значения~масс,~найдём~ускорение:</math> | ||
| + | ::<math>a=\frac{0{,}06~кг-0{,}054~кг}{0{,}06~кг+0{,}054~кг} \cdot 9{,}81~м/c^2=0{,}51~м/c^2</math> | ||
| + | |||
| + | ::<math>Ответ:а=0{,}51 м/c^2</math> | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
| + | |||
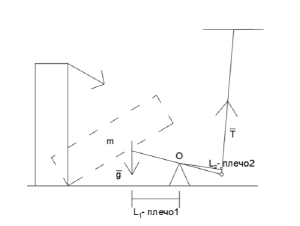
| + | *Расчёт силы натяжения нити (Хайбулина О.) | ||
| + | <div class="mw-collapsible mw-collapsed"> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | [[File:Zadacha 10.png|thumb|Расчет силы натяжения нити]] | ||
| + | ::<math>Дано:</math> | ||
| + | ::<math>m=0{,}106~кг</math> | ||
| + | ::<math>L_{1}=10~см</math> | ||
| + | ::<math>L_{2}=7{,}5~см</math> | ||
| + | |||
| + | ::<math>Найти:~T</math> | ||
| + | |||
| + | ::<math>Решение:</math> | ||
| + | ::<math>Используем ~закон ~сохранения ~моментов ~сил ~(ЗСМС):</math> | ||
| + | ::<math>В ~нашем ~случае: ~M_{1}=M_{2}:</math> | ||
| + | ::<math>m \cdot g \cdot L_{1}=T \cdot L_{2}</math> | ||
| + | ::<math>T=m \cdot g \cdot \frac {L_{1}}{L_{2}}</math> | ||
| + | ::<math>Подставляем ~численные ~значения ~и ~получаем ~T:</math> | ||
| + | ::<math>T=1{,}385~Н</math> | ||
| + | |||
| + | ::<math>Ответ:T=1{,}385~Н. </math> | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
| + | |||
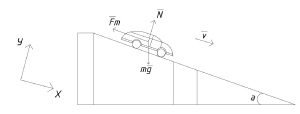
| + | *Расчёт коэффициента трения машинки с наклонной плоскостью (Филиппенкова А.) | ||
| + | <div class="mw-collapsible mw-collapsed"> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | [[File:Расчёт коэффициента трения машинки с наклонной плоскостью.png|thumb|Расчёт коэффициента трения машинки с наклонной плоскостью]] | ||
| + | ::<math>Дано:</math> | ||
| + | ::<math>α=30°~</math> | ||
| + | ::<math>h=0{,}1~м</math> | ||
| + | ::<math>t=0{,}3~c</math> | ||
| + | |||
| + | ::<math>Найти:~μ</math> | ||
| + | |||
| + | ::<math>Решение:</math> | ||
| + | ::<math>Используя ~второй ~закон ~Ньютона:</math> | ||
| + | ::<math>m \cdot \vec{g} + \vec{F_{тр}}+ \vec{N}= m \cdot \vec{a}</math> | ||
| + | ::<math>Перепишем ~с ~учетом~ проекций~ на~ ось~ Ox:</math> | ||
| + | ::<math>m \cdot g \cdot sin{α} - F_{тр}=m \cdot a</math> | ||
| + | ::<math>Перепишем ~с ~учетом~ проекций~ на~ ось~ Oy:</math> | ||
| + | ::<math>N- m \cdot g \cdot cos{α} = 0</math> | ||
| + | ::<math>F_{тр}= μ \cdot N</math> | ||
| + | ::<math>a= g \cdot sin{α} - g \cdot μ \cdot cos{α}</math> | ||
| + | ::<math>S= \frac {a \cdot t^2}{2}</math> | ||
| + | ::<math>t= \sqrt({\frac{2 \cdot S}{a}})</math> | ||
| + | ::<math>Из ~прямоугольного ~треугольника ~АВС:</math> | ||
| + | ::<math>sin{α}=\frac {h}{S}</math> | ||
| + | ::<math>S=\frac {h}{sin{α}}</math> | ||
| + | ::<math>t=\sqrt({\frac {2 \cdot h}{sin{α} \cdot g \cdot(sin{α}-μ \cdot cos{α})}})</math> | ||
| + | ::<math>Подставив~численные~значения,~получим:</math> | ||
| + | ::<math>μ=0{,}04</math> | ||
| + | |||
| + | ::<math>Ответ:μ=0{,}04. </math> | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
| + | |||
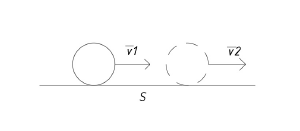
| + | *Расчёт конечной скорости шарика при прохождении пути S (Шестаков Д.) | ||
| + | <div class="mw-collapsible mw-collapsed"> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | [[File:Расчет конечной скорости шарика при прохождении пути S.png|thumb|Расчет конечной скорости шарика при прохождении пути S]] | ||
| + | ::<math>Дано:</math> | ||
| + | ::<math>v_{1}=0{,}5~м/с~</math> | ||
| + | ::<math>S=0{,}07~м</math> | ||
| + | ::<math>t=0{,}15~c</math> | ||
| + | |||
| + | ::<math>Найти:~v_{2}</math> | ||
| + | |||
| + | ::<math>Решение:</math> | ||
| + | ::<math>Из~уравнения~равнозамедленного~движения:</math> | ||
| + | ::<math>S=v \cdot t-\frac{a \cdot t^2}{2}</math> | ||
| + | ::<math>a=\frac{2 \cdot(v \cdot t - S)}{t^2}</math> | ||
| + | ::<math>v_{2}=v_{1}+a \cdot t</math> | ||
| + | ::<math>v_{2}=v_{1}+ \frac{2 \cdot(v \cdot t - S)}{t^2}</math> | ||
| + | ::<math>v_{2}=v_{1}+2 \cdot v_{1} - \frac{S}{t}</math> | ||
| + | ::<math>Таким~образом,~конечная~скорость~рассчитывается~по~формуле:</math> | ||
| + | ::<math>v_{2}=3 \cdot v_{1} - \frac{S}{t}</math> | ||
| + | ::<math>Подставив~численные~значения,~получим:</math> | ||
| + | ::<math>v_{2}=1{,}033~м/c</math> | ||
| + | |||
| + | ::<math>Ответ:v_{2}=1{,}033~м/c</math> | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
| + | |||
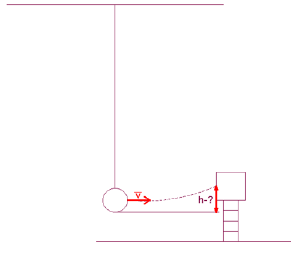
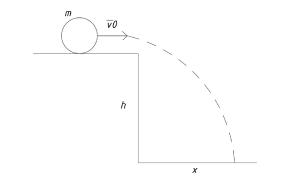
| + | *Расчёт длины полёта шарика до кнопки (Данилова Д.) | ||
| + | <div class="mw-collapsible mw-collapsed"> | ||
| + | <div class="mw-collapsible-content"> | ||
| + | [[File:Расчет длины полета шарика до кнопки.png|thumb|Расчет длины полета шарика до кнопки]] | ||
| + | ::<math>Дано:</math> | ||
| + | ::<math>v_{0}=1{,}033~м/с~</math> | ||
| + | ::<math>h=0{,}07~м</math> | ||
| + | |||
| + | ::<math>Найти:~x~</math> | ||
| + | |||
| + | ::<math>Решение:</math> | ||
| + | ::<math>Рассмотрим~систему~уравнений:</math> | ||
| + | ::<math>x=v_{0} \cdot t</math> | ||
| + | ::<math>y=y_{0}- \frac{g \cdot t^2}{2}</math> | ||
| + | ::<math>Тогда:</math> | ||
| + | ::<math>h=\frac{g \cdot t^2}{2}</math> | ||
| + | ::<math>t=\sqrt{\frac{2h}{g}}</math> | ||
| + | ::<math>Следовательно:</math> | ||
| + | ::<math>x=v_{0} \cdot \sqrt{\frac{2h}{g}}</math> | ||
| + | ::<math>Подставив~численные~значения,~получим:</math> | ||
| + | ::<math>x=0{,}15~м</math> | ||
| + | |||
| + | ::<math>Ответ:x=0{,}15~м</math> | ||
| + | |||
| + | </div> | ||
</div> | </div> | ||
==Результаты по проекту== | ==Результаты по проекту== | ||
| − | Машина Голдберга выполняет необходимую задачу: нажимает на кнопку для | + | Машина Голдберга выполняет необходимую задачу: нажимает на дистанционную кнопку для создания фотоснимка. В процессе расчетов и пробных запусков были устранены некоторые этапы и модифицированы существующие конструкции. В ходе вычислений были изменены некоторые параметры установки и исправлены неполадки. |
| − | Видео | + | Видео рабочего процесса создания машины Голдберга. |
| − | {{#widget:YouTube|id= | + | {{#widget:YouTube|id=NZYKrm9Clnk}} |
| − | Видео | + | Видео всех этапов Машины Голдберга. |
| − | {{#widget:YouTube|id= | + | {{#widget:YouTube|id=G4aPihxHQi0}} |
==Литература и ссылки== | ==Литература и ссылки== | ||
Текущая версия на 12:12, 15 июня 2019
Машина Голдберга, машина Руба Голдберга, машина Робинсона-Голдберга, Машина Робинсона или заумная машина — это устройство, которое выполняет очень простое действие чрезвычайно сложным образом — как правило, посредством длинной последовательности взаимодействий по «принципу домино». По принципу работы Машины Голдберга мы собираем установку "Фотоаппарат Голдберга".
Содержание
Описание[править]
Актуальность[править]
Данный проект является актуальным за счет того, что при создании данной машины Голдберга можно найти практическое применение курсу теоретической механики, развить прикладные способности, а также научиться использовать разнообразное оборудование.
Цель проекта[править]
Воссоздать машину Голдберга, результатом работы которой будет осуществление фотоснимка.
Задачи проекта[править]
- Обозначить последовательность действий, которые будут выполняться машиной Голдберга
- Создать схему Машины Голдберга.
- Создать цифровую модель данной установки
- Подобрать необходимые материалы и инструменты для проекта
- Сделать отдельные этапы проекта
- Произвести необходимые расчеты и вычисления для определения параметров отдельных частей проекта.
- Собрать воедино все этапы Машины Голдберга.
- Произвести пробные запуски и устранить недочеты.
- Смонтировать видео.
- Произвести показательный запуск Машины Голдберга.
- Создать вики-страницу проекта
Проектная команда[править]
Группа 13131/8
- Войтенко Мария
- Вишнев Артем
- Данилова Дарья
- Доенина Анна
- Егунова Анастасия
- Ефимов Евгений
- Лось Полина
- Нахимовский Алексей
- Панова Юлия
- Савчиков Артем
- Сиротина Анастасия
- Филиппенкова Алина
- Хайбулина Олеся
- Шестаков Данил
Работа по проекту[править]
Действия, выполняемые машиной Голдберга[править]
- Запуск резинки, толкающей машинку
- Машинка совершает элемент "мертвая петля" на трассе
- Машинка толкает шарик
- Шарик скатывается по наклонной плоскости и толкает маятник
- Маятник толкает домино
- В процессе падают все доминошки
- Последняя из домино толкает брусок
- Брусок толкает машинку
- Машинка толкает кубик
- Кубик падает на рычаг
- Рычаг поднимается с другой стороны
- Блок перевешивает на другую сторону
- Груз блока толкает шарик
- Шарик катится и падает на кнопку
- Совершается фотоснимок
Материалы и предметы для создания проекта[править]
- Мячики
- Элемент "мертвая петля"
- 2 машинки
- Рычаг
- Нить
- Фанера
- Доски
- Клей
- Кегля
- Стул
- Неподвижный блок
- Резинка
- Кнопка дистанционного управления
- Домино
- Скотч
Инструменты для создания проекта[править]
- Лобзик электрический
- Напильник ручной
- Шуруповерт
- Клеевой пистолет
- Молоток
Этапы создания проекта[править]
| Срок | Задачи | Возникающие проблемы | Что сделано к сроку |
| 05.03.19 | Обсуждение этапов работы Машины Голдберга | Возникновение разногласий по поводу последовательности действий, этапов машины | Нахождение оптимальной схемы машины, создание чернового варианта модели |
| 19.03.19 | Утверждение этапов модели, создание списка материалов и распределение по мини-группам | Неравномерное распределение по группам; прения по поводу того, на чем будет машина стоять, сколько места займет и на каких этапах потребуются более высокие конструкции | Определение наиболее подходящего распределения по группам, распределение задач и постановка целей; нахождение компромисса по поводу спорных моментов |
| 02.04.19 | Нахождение материалов, создание начальных этапов | Проблематичность обеспечения некоторыми изначально включенными в список материалами, количество провальных запусков машины на первых этапах, преобладавшее над удачными | Замена труднодоставаемых материалов другими ("мёртвой" петли, изначально планировавшейся быть напечатанной на 3D-принтере, на установку из детского набора), возникновение понимания того, как лучше всего дать машинке старт, создание "бортиков" на 2 этапе, дабы обеспечить удачный спуск машинки |
| 15.04.19 | Окончательное создание первых этапов установки и контроль их работы | Неполная работоспособность установки, в следствие чего возникла необходимость замены некоторых материалов | Первые этапы установки находятся в рабочем состояние примерно на 75% |
| 16.04.19 | Сбор отдельных этапов установки, требующих наиболее прикладную составляющую, и проверка их на работоспособность, примерный расчёт необходимых параметром для этих этапов | Нехватка материалов, поэтому необходимость докупать материалы; появление необходимости получения навыков работы с прикладными инструментами | Первые этапы установки готовы и работают в идеальном состоянии, частично созданы последующие этапы машины |
| 29.04.19 | Сбор всех этапов установки в единое целое, проверка их работоспособности | Наличие недочетов в работе установки | Установка практически приобрела свой окончательный вид |
| 30.04.19 | Повторный, полный сбор установки с устранением выявленных неполадок | Практически не возникло, были убраны небольшие недочеты, чтобы установка работала каждый раз в штатном режиме | Окончательно готовая установка |
| 14.05.19 | Проведение контрольных запусков машины, оформление вики-страницы | Трудности при создание вики-страницы из-за не знания языка программирования | Удачное прохождение машиной всех этапов, создание фотографий посредством её; приобретение необходимые знаний по оформлению вики-страницы, преодоление трудностей |
Расчёты элементов проекта[править]
- Расчёт скорости машины, с которой она поедет при запуске пружины (Войтенко М.)
- Расчёт скорости машинки при соударении с шариком (Егунова А.)
- Расчёт скорости мяча, приобретенной в результате упругого соударения с машиной (Доенина А.)
- Расчёт скорости шара в конце наклонной плоскости (Ефимов Е.)
- Расчёт оптимальной массы шарика, необходимой для поднятия после удара на высоту h (Лось П.)
- Расчёт оптимальной высоты подъема шарика (Панова Ю.)
- Расчёт скорости кубика, приобретённой в результате cоударения с шариком на нити (Вишнев А.)
- Расчёт скорости домино (Савчиков А.)
- Расчёт скорости бруска, приобретенной в результате соударения (Нахимовский А.)
- Расчёт ускорения, с которым груз, перекинутый через неподвижный блок, падает на машину (Сиротина А.)
- Расчёт силы натяжения нити (Хайбулина О.)
- Расчёт коэффициента трения машинки с наклонной плоскостью (Филиппенкова А.)
- Расчёт конечной скорости шарика при прохождении пути S (Шестаков Д.)
- Расчёт длины полёта шарика до кнопки (Данилова Д.)
Результаты по проекту[править]
Машина Голдберга выполняет необходимую задачу: нажимает на дистанционную кнопку для создания фотоснимка. В процессе расчетов и пробных запусков были устранены некоторые этапы и модифицированы существующие конструкции. В ходе вычислений были изменены некоторые параметры установки и исправлены неполадки.
Видео рабочего процесса создания машины Голдберга.
Видео всех этапов Машины Голдберга.
Литература и ссылки[править]
- Инструкция по оказанию первой доврачебной помощи
- Инструкция по охране труда при работе с ручным инструментом
- Как создать машину Руба Голдберга самому
- Краткая теория по теоретической механике
- Машина Голдберга
- Методическое пособие по использованию 3D принтера DFKit
- Методическое пособие по использованию ЧПУ лазерного станка DFKit
- Примеры различных машин Голдберга:
75 Rube Goldberg Ideas & Inventions | DoodleChaos The Dresser - Rube Goldberg Machine for Getting Dressed | Joseph's Machines Marble run | Vivify cg Мастерская Голдберга | СПб и Мск | Лекториум