Колебания одномерной цепочки — различия между версиями
Loban9614 (обсуждение | вклад) (→Анализ результатов) |
Loban9614 (обсуждение | вклад) (→Решение задачи) |
||
| (не показано 6 промежуточных версий этого же участника) | |||
| Строка 15: | Строка 15: | ||
===Решение задачи=== | ===Решение задачи=== | ||
| − | Рассмотрим модель колебаний одномерной многоатомной цепочки равных масс. Пусть в этой цепочке находится N атомов. Обозначим смещение n-го атома | + | Рассмотрим модель колебаний одномерной многоатомной цепочки равных масс. Пусть в этой цепочке находится N атомов. Обозначим смещение n-го атома <math> u_{n} </math>, а атома, отстоящего от него на p узлов, <math> u_{n+p} </math> . Примем в качестве положительных смещения атомов вправо от положения равновесия, а отрицательных – влево. |
Каждый атом смещается только вдоль цепочки, что следует из требования одномерности модели. Пусть атомы связаны между собой упругой силой, соответствующей потенциалу Леннарда-Джонса с коэффициентом упругости С. | Каждый атом смещается только вдоль цепочки, что следует из требования одномерности модели. Пусть атомы связаны между собой упругой силой, соответствующей потенциалу Леннарда-Джонса с коэффициентом упругости С. | ||
| Строка 21: | Строка 21: | ||
F(r) = \frac{12D}{a}\left[-\left(\frac{a}{r}\right)^{13} + \left(\frac{a}{r}\right)^{7}\right]. | F(r) = \frac{12D}{a}\left[-\left(\frac{a}{r}\right)^{13} + \left(\frac{a}{r}\right)^{7}\right]. | ||
</math> | </math> | ||
| − | Найдем уравнение движения n-го и n+1-го атома в цепи. В равновесном положении силы, действующие на атомы, равны нулю. При | + | Найдем уравнение движения n-го и n+1-го атома в цепи. В равновесном положении силы, действующие на атомы, равны нулю. При смещениях на каждый n-й атом будет действовать сила со стороны соседних атомов. |
::<math> | ::<math> | ||
| − | m\ddot{r}=-\ | + | m\ddot{r}_{i}=-\nablaП_{i} |
</math> | </math> | ||
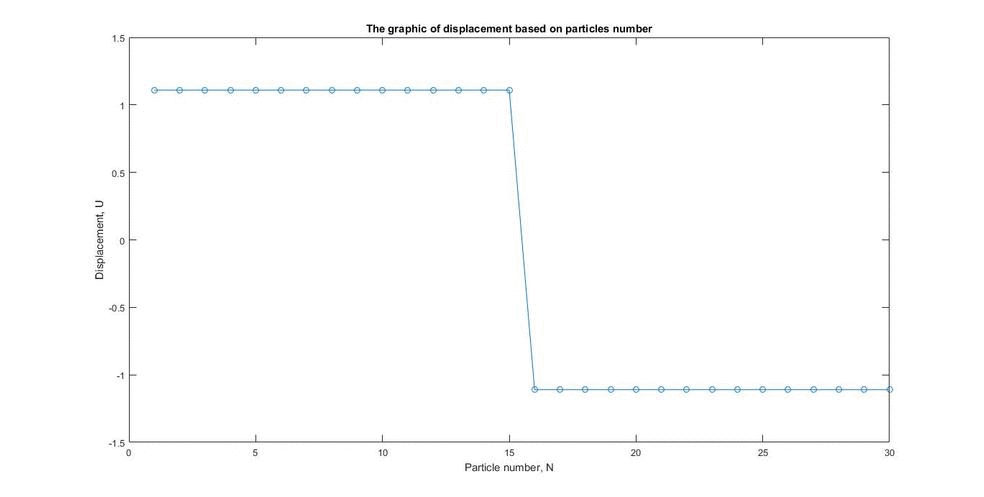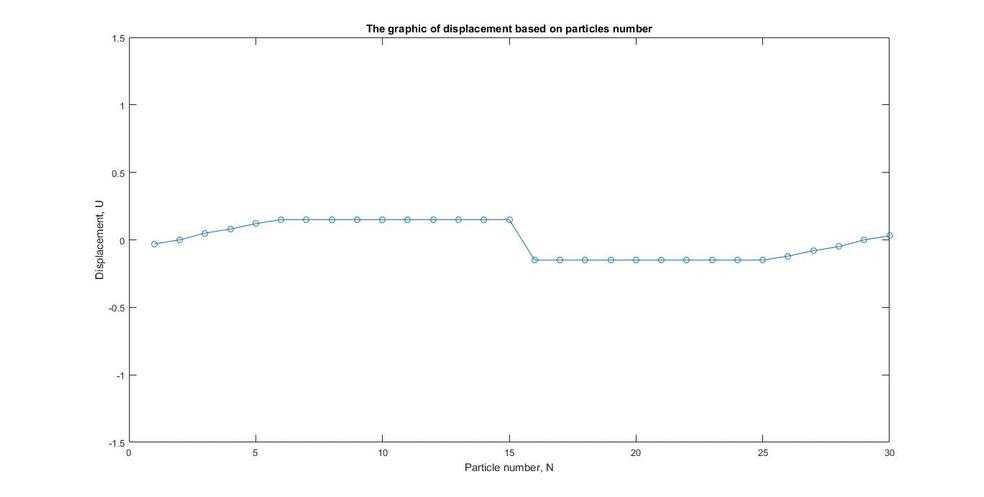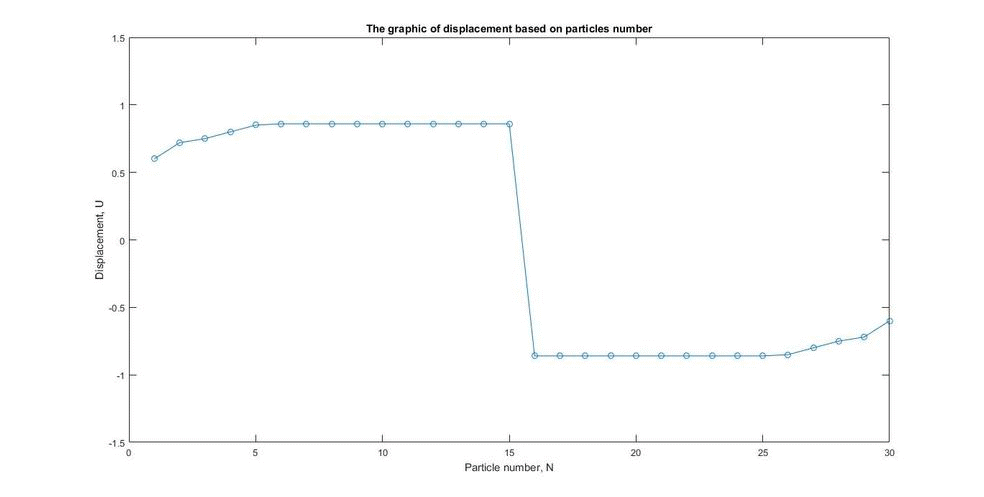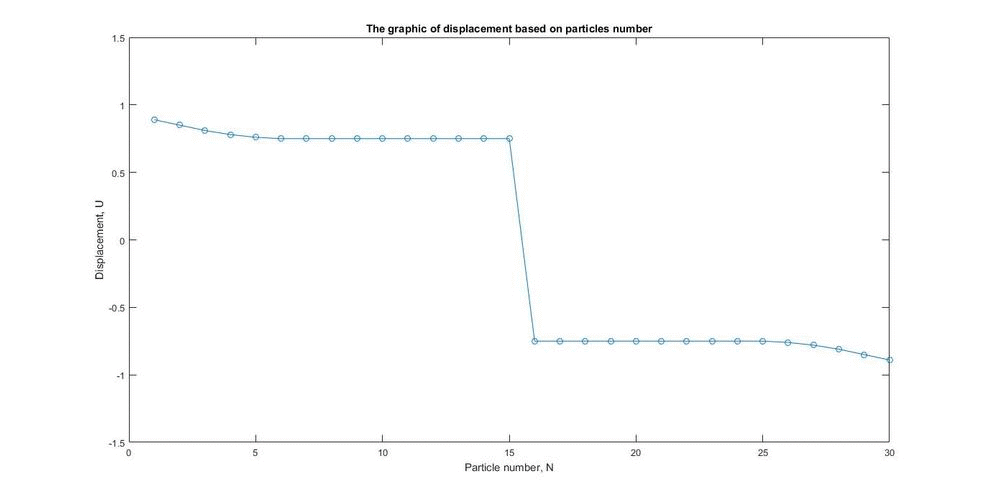
| − | В качестве начальных условий | + | В качестве начальных условий имеем растянутую цепочку,перемещения всех частиц в начальный момент времени равны 1,11. |
| − | === | + | ===Результаты=== |
| − | + | [[File:Webp.net-gifmaker_(5).gif]] | |
| − | [[File: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== См. также == | == См. также == | ||
Текущая версия на 02:25, 1 марта 2019
Курсовые работы 2018-2019 учебного года > Колебания одномерной цепочкиКурсовой проект по Механике дискретных сред
Исполнитель: Лобанов Илья
Группа: 43604/1
Семестр: осень 2018
Постановка задачи[править]
Рассматривается цепочка из N материальных частиц P0, P1, ... Pn, ..., PN–1, каждая из которых обладает одинаковой массой m. Частицы соединены пружинками. Рассматриваются продольные колебания образующих цепочку частиц, при условии, что взаимодействие задается с помощью потенциала Леннарда-Джонса.
Период одного колебания:
Решение задачи[править]
Рассмотрим модель колебаний одномерной многоатомной цепочки равных масс. Пусть в этой цепочке находится N атомов. Обозначим смещение n-го атома , а атома, отстоящего от него на p узлов, . Примем в качестве положительных смещения атомов вправо от положения равновесия, а отрицательных – влево.
Каждый атом смещается только вдоль цепочки, что следует из требования одномерности модели. Пусть атомы связаны между собой упругой силой, соответствующей потенциалу Леннарда-Джонса с коэффициентом упругости С.
Найдем уравнение движения n-го и n+1-го атома в цепи. В равновесном положении силы, действующие на атомы, равны нулю. При смещениях на каждый n-й атом будет действовать сила со стороны соседних атомов.
В качестве начальных условий имеем растянутую цепочку,перемещения всех частиц в начальный момент времени равны 1,11.