Изгиб балки с V-model взаимодействием — различия между версиями
Iagb (обсуждение | вклад) (Новая страница: « Курсовые работы 2018-2019 учебного года > '''Изгиб балки c V-mod…») |
Iagb (обсуждение | вклад) |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 19: | Строка 19: | ||
Также введём два вектора | Также введём два вектора | ||
| − | + | <math> \mathbf{r}_{ij}=\mathbf{r}_i - \mathbf{r}_j </math> | |
| − | \mathbf{r}_{ij}=\mathbf{r}_i - \mathbf{r}_j | + | |
| − | \mathbf{e}_{ij} = \mathbf{r}_{ij} / r_{ij} | + | <math> \mathbf{e}_{ij} = \mathbf{r}_{ij} / r_{ij} </math> |
| − | </math> | ||
Вектор <math>\mathbf{D}_{ij}</math> - соединяет базисы, связанные с соответствующими частицами, поэтому в данной постановке | Вектор <math>\mathbf{D}_{ij}</math> - соединяет базисы, связанные с соответствующими частицами, поэтому в данной постановке | ||
| Строка 28: | Строка 27: | ||
Потенциальная энергия связи: | Потенциальная энергия связи: | ||
| + | [[Файл:Fig2_single_bond.png|350px|thumb|right| Взаимодействие двух частиц]] | ||
| + | |||
<math> | <math> | ||
U = \frac{B_1}{2}(D_{ij}-a)^2 + \frac{B_2}{2}(\mathbf{n}_{j1}-\mathbf{n}_{i1})\cdot\mathbf{d}_{ij} | U = \frac{B_1}{2}(D_{ij}-a)^2 + \frac{B_2}{2}(\mathbf{n}_{j1}-\mathbf{n}_{i1})\cdot\mathbf{d}_{ij} | ||
| Строка 34: | Строка 35: | ||
Таким образом, уравнения для сил и моментов принимают следующий вид: | Таким образом, уравнения для сил и моментов принимают следующий вид: | ||
| + | |||
<math> | <math> | ||
\mathbf{M}^{TB} = B_3 \mathbf{n}_{j1} \times \mathbf{n}_{i1} - \frac{B_4}{2}(\mathbf{n}_{j2}\times\mathbf{n}_{i2} + \mathbf{n}_{j3}\times\mathbf{n}_{i3}) | \mathbf{M}^{TB} = B_3 \mathbf{n}_{j1} \times \mathbf{n}_{i1} - \frac{B_4}{2}(\mathbf{n}_{j2}\times\mathbf{n}_{i2} + \mathbf{n}_{j3}\times\mathbf{n}_{i3}) | ||
| Строка 48: | Строка 50: | ||
</math><br /> | </math><br /> | ||
| − | Для балки с короткими связями между частицами параметры модели принимают следующие | + | Для балки с короткими связями между частицами параметры модели принимают следующие значения: |
| + | |||
<math> | <math> | ||
B_1 = \frac{ES}{a} | B_1 = \frac{ES}{a} | ||
| Строка 63: | Строка 66: | ||
</math><br /> | </math><br /> | ||
| + | ===Алгоритм=== | ||
| + | |||
| + | На каждом временном шагу для каждой из частиц суммируются силы и моменты её взаимодействия с соседними частицами. Далее по второму закону Ньютона вычисляются ускорение и угловое ускорение. Координаты частицы и угловая скорость интегрируются методом Leapfrog. Далее по известному значению угловой скорости интегрируется кватернион вращения частицы и осуществляется поворот её базиса(n). | ||
| + | |||
| + | <math> L(t + \Delta t) = L(t) + \frac{1}{2}\omega(t + \Delta t) \circ L(t) | ||
| + | </math><br /> | ||
| + | |||
| + | <math> n(t + \Delta t) = L(t + \Delta t) \circ n(0) \circ L'(t + \Delta t) | ||
| + | </math><br /> | ||
| + | |||
| + | |||
| + | По вышеизложенным формулам была написана программа на языке Python 3.6.0. Программа генерирует цепочку частиц, задаёт соседей для каждой из частиц, | ||
| + | проводит вычисления положений частиц и их базисов по описанному алгоритму. Далее все перечисленный данные на каждом временном шаге записываются в файл | ||
| + | формата .xyz и их визуализация происходит в программе Open Visualisation Tool путём последовательного отображения частиц на каждом временном шаге. | ||
| + | |||
| + | ===Результаты=== | ||
| + | |||
| + | Расчёты производились при использовании физических параметров стали: | ||
| + | |||
| + | * плотность ρ ≈ 7,86 г/см<sup>3</sup>; | ||
| + | * модуль Юнга ''E'' = 210 ГПа; | ||
| + | * модуль сдвига ''G'' = 80 ГПа; | ||
| + | * коэффициент Пуассона ν = 0,28; | ||
| + | |||
| + | Рассматривалась балка круглого сечения радиусом r = 5 см, длиной l = 5 м, прикладываемая сила F = 10000 Н, количество частиц - 21. | ||
| + | |||
| + | * Закреплённый правый край балки, сила приложена к левому краю | ||
| + | [[Файл:beam1.gif]] | ||
| + | * Закреплены оба края, сила приложена к середине балки | ||
| + | [[Файл:beam2.gif]] | ||
== Ссылки == | == Ссылки == | ||
Текущая версия на 14:24, 28 января 2019
Курсовые работы 2018-2019 учебного года > Изгиб балки c V-model взаимодействиемКурсовой проект по Механике дискретных сред
Исполнитель: Абрамов Игорь
Группа: 43604/1
Семестр: осень 2018
Содержание
Постановка задачи[править]
Создание модели и визуализация изгиба балки с V-model взаимодействием.
Решение[править]
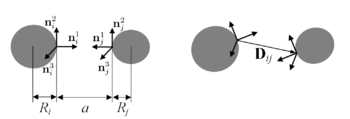
Балка моделируется как система частиц, каждая из которых взаимодействует с двумя ближайшими соседями. Для ориентация каждой ой частицы в пространстве используется жёстко связанный с ней в центре частицы базис . Также введём два вектора
Вектор - соединяет базисы, связанные с соответствующими частицами, поэтому в данной постановке он равен . Вектор - единичный, сонаправленный .
Потенциальная энергия связи:
Таким образом, уравнения для сил и моментов принимают следующий вид:
Для балки с короткими связями между частицами параметры модели принимают следующие значения:
Алгоритм[править]
На каждом временном шагу для каждой из частиц суммируются силы и моменты её взаимодействия с соседними частицами. Далее по второму закону Ньютона вычисляются ускорение и угловое ускорение. Координаты частицы и угловая скорость интегрируются методом Leapfrog. Далее по известному значению угловой скорости интегрируется кватернион вращения частицы и осуществляется поворот её базиса(n).
По вышеизложенным формулам была написана программа на языке Python 3.6.0. Программа генерирует цепочку частиц, задаёт соседей для каждой из частиц,
проводит вычисления положений частиц и их базисов по описанному алгоритму. Далее все перечисленный данные на каждом временном шаге записываются в файл
формата .xyz и их визуализация происходит в программе Open Visualisation Tool путём последовательного отображения частиц на каждом временном шаге.
Результаты[править]
Расчёты производились при использовании физических параметров стали:
- плотность ρ ≈ 7,86 г/см3;
- модуль Юнга E = 210 ГПа;
- модуль сдвига G = 80 ГПа;
- коэффициент Пуассона ν = 0,28;
Рассматривалась балка круглого сечения радиусом r = 5 см, длиной l = 5 м, прикладываемая сила F = 10000 Н, количество частиц - 21.
- Закреплённый правый край балки, сила приложена к левому краю
- Закреплены оба края, сила приложена к середине балки