Машина Голдберга, разбивающая яйцо в сковородку — различия между версиями
(→Расчеты) |
(→Инструменты) |
||
| (не показаны 24 промежуточные версии 4 участников) | |||
| Строка 149: | Строка 149: | ||
* Пассатижи | * Пассатижи | ||
| − | |||
===Этапы создания проекта=== | ===Этапы создания проекта=== | ||
| Строка 188: | Строка 187: | ||
==Расчеты== | ==Расчеты== | ||
| − | * Расчет сообщающихся сосудов | + | *Расчет сообщающихся сосудов |
Для работы будем использовать 2 одинаковых цилиндрических сообщающихся сосуда с водой и резиновый шарик, который так же заполнен водой. Объем каждого сосуда = 4 л. Диаметр дна сосудов = 16 см. Высота стенок сосудов = 20 см. Шарик лопается, и вся вода из него попадает в первый сосуд. Необходимо, чтобы уровень воды во втором сосуде поднялся на 5 см. Найдем объем воды, который должен находиться в шарике. | Для работы будем использовать 2 одинаковых цилиндрических сообщающихся сосуда с водой и резиновый шарик, который так же заполнен водой. Объем каждого сосуда = 4 л. Диаметр дна сосудов = 16 см. Высота стенок сосудов = 20 см. Шарик лопается, и вся вода из него попадает в первый сосуд. Необходимо, чтобы уровень воды во втором сосуде поднялся на 5 см. Найдем объем воды, который должен находиться в шарике. | ||
| − | + | V– начальный объем воды в первом сосуде | |
| − | + | V<sub>2</sub> – начальный объем воды во втором сосуде | |
| − | + | V<sub>ball</sub> – объем воды, находящейся в шарике | |
| − | + | H<sub>1</sub> = 10 см – начальная высота столбика воды в первом сосуде | |
| − | + | H<sub>2</sub> = 10 см – начальная высота столбика воды во втором сосуде | |
| − | V | + | V'<sub>1</sub> – конечный объем воды в первом сосуде |
| − | V | + | V'<sub>2</sub> – конечный объем воды во втором сосуде |
| − | H | + | H'<sub>1</sub> – конечная высота столбика воды в первом сосуде |
| + | H'<sub>2</sub>- конечная высота столбика воды во втором сосуде | ||
| − | + | S – площадь сечения сосудов | |
| − | + | Давление жидкости в сосуде расписывается по формуле: P=pgH | |
| + | Отношение уровней жидкостей обратно пропорционально отношению их плотностей, то есть | ||
| + | p<sub>1</sub>/p<sub>2</sub>= H<sub>1</sub>/H<sub>2</sub> | ||
| + | |||
| + | p - плотность жидкости | ||
| + | |||
| + | Н - высота столба воды в сосуде | ||
| − | Определим площадь дна сосудов: S=1/4 | + | Определим площадь дна сосудов: S=1/4 πD_2=0,25*16*16=200 см<sup>2</sup> |
| − | Конечная высота столбика воды во втором сосуде: H | + | Конечная высота столбика воды во втором сосуде: H'<sub>2</sub> = 15 см. |
Закон сообщающихся сосудов: в неподвижных и открытых сообщающихся сосудах любой формы давление жидкости на любом горизонтальном уровне одинаково. | Закон сообщающихся сосудов: в неподвижных и открытых сообщающихся сосудах любой формы давление жидкости на любом горизонтальном уровне одинаково. | ||
| Строка 221: | Строка 227: | ||
Следствие 2: в неподвижных и открытых сообщающихся сосудах однородная жидкость всегда устанавливается на одинаковом уровне независимо от формы сосудов. | Следствие 2: в неподвижных и открытых сообщающихся сосудах однородная жидкость всегда устанавливается на одинаковом уровне независимо от формы сосудов. | ||
| − | Следовательно, | + | Следовательно, H<sub>1</sub> = H<sub>2</sub> = 10 см, H'<sub>1</sub> = H'<sub>2</sub> = 15 см и V1 = V2 , V'<sub>1</sub> = V'<sub>2</sub> |
Вода из лопнувшего шарика выльется в первый сосуд. Затем часть воды через перемычку перельется во второй сосуд. | Вода из лопнувшего шарика выльется в первый сосуд. Затем часть воды через перемычку перельется во второй сосуд. | ||
| Строка 227: | Строка 233: | ||
Суммарный объем воды в двух сосудах: | Суммарный объем воды в двух сосудах: | ||
| − | + | V<sub>1</sub> + V<sub>2</sub> + V<sub>ball</sub> = V'<sub>1</sub> + V'<sub>2</sub>. | |
| − | S* | + | S*H<sub>1</sub> + S*H<sub>2</sub> + Vball= S*H'<sub>1</sub> + S*H'<sub>2</sub>. |
| − | 2S* | + | 2S*H<sub>1</sub> + V<sub>ball</sub> = 2S*H'<sub>1</sub>. |
Объем воды в шарике должен быть равен: | Объем воды в шарике должен быть равен: | ||
| − | + | Vball= 2S*H'<sub>1</sub> - 2S*H<sub>1</sub> = 2*200*15 - 2*200*10 = 2000 см<sup>3</sup> | |
| + | |||
<gallery> | <gallery> | ||
| − | A-A1wrKO2tg.jpg| | + | A-A1wrKO2tg.jpg|Сообщающиеся сосуды |
| − | |||
</gallery> | </gallery> | ||
| − | |||
* Расчет "качели" | * Расчет "качели" | ||
| Строка 249: | Строка 254: | ||
Тогда уравнение моментов выглядит вот так: | Тогда уравнение моментов выглядит вот так: | ||
| − | (1.2 ρlg) * 0.6lcos(a) = (ρlg)* 0.5lcos(a) + ( | + | (1.2 ρlg) * 0.6lcos(a) = (ρlg)* 0.5lcos(a) + (M<sub>b</sub> + M<sub>w</sub>)g * 0.9lcos(a) + N*1.2lcos(a) |
В тот момент, когда домино падает, N = 0 | В тот момент, когда домино падает, N = 0 | ||
| − | (1.2 ρlg) * 0.6lcos(a) = (ρlg)* 0.5lcos(a) + ( | + | (1.2 ρlg) * 0.6lcos(a) = (ρlg)* 0.5lcos(a) + (M<sub>b</sub> + M<sub>w</sub>)g * 0.9lcos(a) |
Сократим: | Сократим: | ||
| − | (1.2 ρl) * 0.6 = (ρl)* 0.5 + ( | + | (1.2 ρl) * 0.6 = (ρl)* 0.5 + (M<sub>b</sub> + M<sub>w</sub>) * 0.9 |
Тогда масса воды, необходимая для переворачивания качели: | Тогда масса воды, необходимая для переворачивания качели: | ||
| − | + | M<sub>w</sub> = (0.22 ρl – 0.9M<sub>b</sub>)/(0.9) | |
Масса целой дощечки (1.2+1) ρl = 20г, а значит ρl = 9.09г | Масса целой дощечки (1.2+1) ρl = 20г, а значит ρl = 9.09г | ||
| Строка 267: | Строка 272: | ||
Масса колпачка 1г | Масса колпачка 1г | ||
| − | Тогда | + | Тогда M<sub>w</sub> = (0.22 * 9.09 – 0.9*1)/(0.9) = 1.22г |
| + | |||
| + | <gallery> | ||
| + | vNWOFszA4Tg.jpg|Качель | ||
| + | </gallery> | ||
| + | |||
| + | * Расчет "скорость машинки" | ||
| + | |||
| + | Машинка привязана к натянутой пружине и зафиксирована с другой стороны ниткой (рис. 1): | ||
| + | |||
| + | m = 0,5кг (масса машинки) | ||
| + | |||
| + | x<sub>1</sub> = 0,05м (пружина в состоянии покоя) | ||
| + | |||
| + | x<sub>2</sub> = 0,17м (пружина в натянутом состоянии) | ||
| + | |||
| + | Δx = 0,12м | ||
| + | |||
| + | Состояние покоя: | ||
| + | |||
| + | OX: F<sub>упр</sub> – T = 0; | ||
| + | |||
| + | OY: N – m*g = 0; | ||
| + | |||
| + | F<sub>упр</sub> = k * Δx (закон Гука) | ||
| + | |||
| + | k = ? | ||
| + | |||
| + | Чтобы найти k, вертикально взвесим машинку на пружине, чтобы уравнять силы упругости и тяжести (рис. 2): | ||
| + | |||
| + | OY: F<sub>упр</sub> – F<sub>тяж</sub> = 0; | ||
| + | |||
| + | F<sub>упр</sub> = F<sub>тяж</sub> | ||
| + | |||
| + | k * Δx = m * g | ||
| + | |||
| + | x<sub>1</sub> = 0,05м | ||
| + | |||
| + | x<sub>2</sub> = 0,07м | ||
| + | |||
| + | Δx = 0,02м | ||
| + | |||
| + | k * 0,02 = 0,5 * 9,8 | ||
| + | |||
| + | k = 0,5 * 9,8 / 0,02 = 245 Н/м | ||
| + | |||
| + | Теперь можем найти силу, с которой поедет машинка после разреза фиксирующей нитки (рис. 3): | ||
| + | |||
| + | OX: m * a = F<sub>упр</sub> | ||
| + | |||
| + | F<sub>упр</sub> = 245 * 0,12 = 29,4 Н | ||
| + | |||
| + | a = 29,4 / 0,5 = 58,8 м/с<sup>2</sup> | ||
| + | |||
| + | v = at | ||
| + | |||
| + | t = 0,1 с | ||
| + | |||
| + | v = 58,8 * 0,1 = 5,88 м/с | ||
| + | |||
| + | Скорость, с которой машинка едет после разреза фиксирующей нитки: 5,88 м/с | ||
| + | |||
| + | <gallery> | ||
| + | Рисунки_к_расчёту.jpg|Рисунки к расчёту | ||
| + | </gallery> | ||
| + | |||
| + | * Принцип домино | ||
| + | |||
| + | 𝑚<sub>1</sub>𝑣<sub>1</sub>+𝑚<sub>2</sub>𝑣<sub>2</sub>= 𝑚<sub>1</sub>𝑣'<sub>1</sub>+𝑚<sub>2</sub>𝑣'<sub>2</sub> | ||
| + | |||
| + | 𝑝<sub>1</sub>+ 𝑝<sub>2</sub>= 𝑝'<sub>1</sub>+𝑝'<sub>2</sub> | ||
| + | |||
| + | 𝑣<sub>1</sub>=5 м/с; | ||
| + | |||
| + | 𝑣<sub>2</sub>=0; | ||
| + | |||
| + | 𝑚<sub>1</sub>= 0,05 кг; | ||
| + | |||
| + | 𝑚<sub>2</sub>=0,01 кг | ||
| + | |||
| + | 𝑝<sub>1</sub>=𝑚<sub>1</sub> | ||
| + | |||
| + | 𝑣<sub>1</sub>−импульс 1 тела до взаимодействия | ||
| + | |||
| + | 𝑝<sub>1</sub>=0.05∗5=0.25 кг м/с | ||
| + | |||
| + | 𝑝<sub>2</sub>=𝑚<sub>2</sub> 𝑣<sub>2</sub>−импульс 2 тела до взаимодействия | ||
| + | |||
| + | 𝑝<sub>2</sub>=0.01∗0=0 кг∗ м/с | ||
| + | |||
| + | 𝑣<sub>1</sub>=3 м/с; | ||
| + | |||
| + | 𝑣<sub>2</sub>=10 м/с | ||
| + | |||
| + | 𝑝'<sub>1</sub>=𝑚<sub>1</sub>𝑣'<sub>1</sub>−Импульс 1 тела после взаимодействия | ||
| + | |||
| + | 𝑝<sub>1</sub>=0.05∗3=0.15кг м/с | ||
| + | |||
| + | 𝑝'<sub>2</sub>=𝑚<sub>2</sub>𝑣'<sub>2</sub>−Импульс 2 тела после взаимодействия | ||
| + | |||
| + | 𝑝<sub>2</sub>=0.01∗10=0.1 кг /мс | ||
| + | |||
| + | Домино нужно сообщить импульс: 𝑝 =0.25 кг м/с | ||
| + | |||
| + | Масса костяшки домино: 𝑚 = 0,01 кг; | ||
<gallery> | <gallery> | ||
| − | + | 27XjOKtbsdM.jpg|Принцип домино | |
| + | </gallery> | ||
| + | * Разбивание яйца о сковородку | ||
| + | <gallery> | ||
| + | d1BvayfwFtQ.jpg|Разбивание яйца | ||
</gallery> | </gallery> | ||
| + | |||
| + | L = 22 см =0,22 м - до сковородки | ||
| + | |||
| + | h = 0,1 м - высота | ||
| + | |||
| + | m=0,05 кг | ||
| + | |||
| + | V<sub>0</sub> = 0 м/с | ||
| + | |||
| + | E<sub>p</sub> = E<sub>p1</sub>+ E<sub>p2</sub> = mgh+mgL = mg(L+h) | ||
| + | |||
| + | E<sub>p</sub> = E<sub>k</sub> = mv/2=mg(L+h) => v = (2mg(L+h)/(m))^(1/2) = (2* 0,05* 9,8 (0,22 * 0,1 ) / (0,05)) ^(1/2) = 2,5 м/с | ||
==Результаты== | ==Результаты== | ||
| − | В ходе создания машины Голдберга были изучены и продемонстрированы многие основные законы теоретической механики. В частности, изучены разделы: статика твёрдого тела, связи и их реакции, моменты сил, кинематика твёрдого тела | + | |
| + | В ходе создания машины Голдберга были изучены и продемонстрированы многие основные законы теоретической механики. В частности, изучены разделы: статика твёрдого тела, связи и их реакции, моменты сил, кинематика твёрдого тела. Созданная машина Голдберга успешно выполняет поставленную задачу, используя сложную, последовательную цепочку действий. | ||
| + | |||
| + | Видео запуска машины Голдберга. | ||
| + | |||
| + | |||
| + | {{#widget:YouTube|id=HB0xDvTWN-M}} | ||
| + | |||
| + | ==Литература и ссылки== | ||
| + | # [https://www.mirf.ru/fun/funny/chto-takoe-mashina-goldberga Что такое машина Голдберга?] | ||
| + | # [https://www.redbull.com/ru-ru/rube-goldberg-machine Машина Голдберга. Что это и зачем?] | ||
| + | # [http://web-local.rudn.ru/web-local/uem/ing/ter_mex/9.pdf Краткий курс теоретической механики] | ||
| + | # [https://ru.wikipedia.org/wiki/Машина_Голдберга Машина Голдберга] | ||
| + | # [https://www.metodolog.ru/node/1910 Машина Рута Голдберга как объект анализа] | ||
| + | # Примеры различных машин Голдберга: | ||
| + | [https://www.youtube.com/watch?v=GOMIBdM6N7Q Переворачиватель страниц] | ||
| + | [https://www.youtube.com/watch?v=qybUFnY7Y8w OK Go - This Too Shall Pass - Rube Goldberg Machine - Official Video] | ||
| + | [https://www.youtube.com/watch?time_continue=4&v=RBOqfLVCDv8 World’s largest Rube Goldberg machine lights up Christmas tree] | ||
| + | [https://www.youtube.com/watch?v=0tRaSUwh5gM Мастерская Голдберга | СПб и Мск | Лекториум] | ||
| + | [https://www.youtube.com/watch?time_continue=7&v=fzlsqGTiEoU The Bet-Losing Machine] | ||
Текущая версия на 02:02, 12 июня 2020
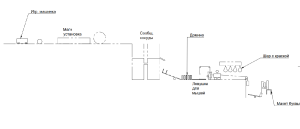
Машина Голдберга (машина Руба Голдберга, машина Робинсона-Голдберга, Машина Робинсона или заумная машина) – это устройство, которое способно выполнять простое действие, используя сложный алгоритм действий. Как правило, последовательность этих действий строится по принципу «домино».
Содержание
Описание проекта[править]
Актуальность проекта[править]
Впервые идея создания сложного механизма для простого действия появилась у художников-карикатуристов в ХХ веке. Такие устройства не утратили актуальности с течением времени из-за самого процесса создания машины. Конструирование машины позволяет наглядно продемонстрировать многие законы теоретической механики и классической физики в действии, а также сделать процесс обучения студентов увлекательным.
Цель[править]
Создать машину Голдберга, которая будет выполнять определённую последовательность действий, в результате которых яйцо будет разбиваться на сковородку.
Задачи проекта[править]
1. Определить последовательность действий, которые будут выполнятся машиной Голдберга
2. Разработать чертёж
3. Произвести необходимые расчёты и вычисления
4. Распределить отдельные части проекта между студентами
5. Создать список материалов и инструментов
6. Собрать отдельные части машины и произвести пробные запуски
7. Проанализировать результаты и исправить ошибки
8. Объединить части и произвести итоговое тестирование
9. Сделать выводы
Проектная команда[править]
- Фаламеев Егор
- Егоров Илья
- Кузьминский Павел
- Пилипчук Константин
- Лучин Федор
- Касатиков Антон
- Примак Любовь
- Абрамова Инга
- Абдукаримов Отабек
- Авдеева Анастасия
- Шурак Анастасия
- Тарасов Андрей
- Шибалов Антон
- Ульянов Сергей
- Немиров Александр
- Колесник Никита
- Маркова Светлана
- Алексеева Ксения
- Ямалиев Валерий
Работа над проектом[править]
Действия, выполняемые машиной[править]
1. Запуск шарика. Реализация работы магнитной пушки.
2. Прокалывание шарика с водой.
3. Наполнение соединяющихся сосудов.
4. Реализация работы качелей.
5. Задействуется принцип работы домино.
6. Запускается мышеловка.
7. Перерезается нить.
8. Запускается машина.
9. Перерезается нить.
10. Запуск яйца.
11. Яйцо разбивается на сковородку.
Материалы[править]
- Гвозди
- Саморезы
- Уголки (40*40*40*1.5)
- Фанера (5, 11, и 15 мм)
- Магниты
- Клей
- Пластиковые бутылки (5л х 2, 0.5л х 1)
- Шарики
- Картон
- Мышеловка
- Изолента
Инструменты[править]
- Лазерный станок
- Фрезерный станок
- Лобзик
- Пила ручная
- Молоток
- Свёрла (3 мм, 3.5 мм)
- Отвертки
- Линейка
- Рулетка
- Карандаш
- Пассатижи
Этапы создания проекта[править]
| Срок | Задача | Возникшие проблемы | Выполненная работа |
|---|---|---|---|
| 27.09.18 | Определить цели и задачи проекта | - | Определена основная цель и выбрана последовательность действий машины |
| 04.10.18 | Разработка чертежа | - | Создан примерный чертеж машины |
| 11.10.18 | Разделение проекта на подзадачи | - | Выявлены основные части, из которых состоит машина |
| 18.10.18 | Произвести расчеты | Отсутствие некоторых данных о параметрах машины | Составлены примерные расчеты |
| 25.10.18 | Создать список необходимых материалов | Ограниченность бюджета. Несоответствие финансовых возможностей потребностям | Пересмотр идеи и внесение изменений в план действий |
| 01.11.18 | Поиск необходимых материалов | Отсутствие понимания об инструментах, необходимых в процессе работы | Составлен итоговый список материалов, получено разрешение на пользование ресурсами Фаблаба |
| 08.11.18 | Продолжение расчетов | Малое количество знаний в области теоретической механики | Закончен поиск необходимой информации |
| 15.11.18 | Первичный сбор частей машины | Несоответствие теоретических и практических данных | Произведен перерасчет |
| 22.11.18 | Оценка данных, полученных на предыдущих этапах работы | - | Проанализирована работа, внесены изменения |
| 29.11.18 | Начало сборки | Отсутствие понимания у людей, что необходимо делать каждому | Разделение группы на две бригады |
| 06.12.18 | Продолжение сборки | - | Определено то, что осталось сделать |
| 13.12.18 | Окончательная сборка и начало тестирования | Работа некоторых частей машины не соответствует ожиданиям | Изменены некоторые моменты проекта |
| 20.12.18 | Итоговое тестирование | - | Подведены итоги |
| 23.12.18 | Сформировать группу людей, ответственных за отчет по работе | - | Группа сформирована |
Расчеты[править]
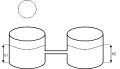
- Расчет сообщающихся сосудов
Для работы будем использовать 2 одинаковых цилиндрических сообщающихся сосуда с водой и резиновый шарик, который так же заполнен водой. Объем каждого сосуда = 4 л. Диаметр дна сосудов = 16 см. Высота стенок сосудов = 20 см. Шарик лопается, и вся вода из него попадает в первый сосуд. Необходимо, чтобы уровень воды во втором сосуде поднялся на 5 см. Найдем объем воды, который должен находиться в шарике.
V– начальный объем воды в первом сосуде
V2 – начальный объем воды во втором сосуде
Vball – объем воды, находящейся в шарике
H1 = 10 см – начальная высота столбика воды в первом сосуде
H2 = 10 см – начальная высота столбика воды во втором сосуде
V'1 – конечный объем воды в первом сосуде
V'2 – конечный объем воды во втором сосуде
H'1 – конечная высота столбика воды в первом сосуде
H'2- конечная высота столбика воды во втором сосуде
S – площадь сечения сосудов
Давление жидкости в сосуде расписывается по формуле: P=pgH Отношение уровней жидкостей обратно пропорционально отношению их плотностей, то есть p1/p2= H1/H2
p - плотность жидкости
Н - высота столба воды в сосуде
Определим площадь дна сосудов: S=1/4 πD_2=0,25*16*16=200 см2
Конечная высота столбика воды во втором сосуде: H'2 = 15 см.
Закон сообщающихся сосудов: в неподвижных и открытых сообщающихся сосудах любой формы давление жидкости на любом горизонтальном уровне одинаково.
Следствие 1: в неподвижных и открытых сообщающихся сосудах высоты столбов жидкостей, отсчитываемые от уровня, ниже которого жидкость однородна, обратно пропорциональны плотностям этих жидкостей.
Следствие 2: в неподвижных и открытых сообщающихся сосудах однородная жидкость всегда устанавливается на одинаковом уровне независимо от формы сосудов.
Следовательно, H1 = H2 = 10 см, H'1 = H'2 = 15 см и V1 = V2 , V'1 = V'2
Вода из лопнувшего шарика выльется в первый сосуд. Затем часть воды через перемычку перельется во второй сосуд.
Суммарный объем воды в двух сосудах:
V1 + V2 + Vball = V'1 + V'2.
S*H1 + S*H2 + Vball= S*H'1 + S*H'2.
2S*H1 + Vball = 2S*H'1.
Объем воды в шарике должен быть равен:
Vball= 2S*H'1 - 2S*H1 = 2*200*15 - 2*200*10 = 2000 см3
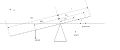
- Расчет "качели"
С левой части на край пластики действует сила реакции опоры N. (см.Рисунок) ρ- линейная плотность дерева, г/метр, тогда целая пластинка имеет массу (1+1.2) ρl = 20г. Масса ёмкости = 1г.
Тогда уравнение моментов выглядит вот так:
(1.2 ρlg) * 0.6lcos(a) = (ρlg)* 0.5lcos(a) + (Mb + Mw)g * 0.9lcos(a) + N*1.2lcos(a)
В тот момент, когда домино падает, N = 0
(1.2 ρlg) * 0.6lcos(a) = (ρlg)* 0.5lcos(a) + (Mb + Mw)g * 0.9lcos(a)
Сократим:
(1.2 ρl) * 0.6 = (ρl)* 0.5 + (Mb + Mw) * 0.9
Тогда масса воды, необходимая для переворачивания качели:
Mw = (0.22 ρl – 0.9Mb)/(0.9)
Масса целой дощечки (1.2+1) ρl = 20г, а значит ρl = 9.09г
Масса колпачка 1г
Тогда Mw = (0.22 * 9.09 – 0.9*1)/(0.9) = 1.22г
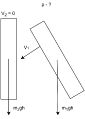
- Расчет "скорость машинки"
Машинка привязана к натянутой пружине и зафиксирована с другой стороны ниткой (рис. 1):
m = 0,5кг (масса машинки)
x1 = 0,05м (пружина в состоянии покоя)
x2 = 0,17м (пружина в натянутом состоянии)
Δx = 0,12м
Состояние покоя:
OX: Fупр – T = 0;
OY: N – m*g = 0;
Fупр = k * Δx (закон Гука)
k = ?
Чтобы найти k, вертикально взвесим машинку на пружине, чтобы уравнять силы упругости и тяжести (рис. 2):
OY: Fупр – Fтяж = 0;
Fупр = Fтяж
k * Δx = m * g
x1 = 0,05м
x2 = 0,07м
Δx = 0,02м
k * 0,02 = 0,5 * 9,8
k = 0,5 * 9,8 / 0,02 = 245 Н/м
Теперь можем найти силу, с которой поедет машинка после разреза фиксирующей нитки (рис. 3):
OX: m * a = Fупр
Fупр = 245 * 0,12 = 29,4 Н
a = 29,4 / 0,5 = 58,8 м/с2
v = at
t = 0,1 с
v = 58,8 * 0,1 = 5,88 м/с
Скорость, с которой машинка едет после разреза фиксирующей нитки: 5,88 м/с
- Принцип домино
𝑚1𝑣1+𝑚2𝑣2= 𝑚1𝑣'1+𝑚2𝑣'2
𝑝1+ 𝑝2= 𝑝'1+𝑝'2
𝑣1=5 м/с;
𝑣2=0;
𝑚1= 0,05 кг;
𝑚2=0,01 кг
𝑝1=𝑚1
𝑣1−импульс 1 тела до взаимодействия
𝑝1=0.05∗5=0.25 кг м/с
𝑝2=𝑚2 𝑣2−импульс 2 тела до взаимодействия
𝑝2=0.01∗0=0 кг∗ м/с
𝑣1=3 м/с;
𝑣2=10 м/с
𝑝'1=𝑚1𝑣'1−Импульс 1 тела после взаимодействия
𝑝1=0.05∗3=0.15кг м/с
𝑝'2=𝑚2𝑣'2−Импульс 2 тела после взаимодействия
𝑝2=0.01∗10=0.1 кг /мс
Домино нужно сообщить импульс: 𝑝 =0.25 кг м/с
Масса костяшки домино: 𝑚 = 0,01 кг;
- Разбивание яйца о сковородку
L = 22 см =0,22 м - до сковородки
h = 0,1 м - высота
m=0,05 кг
V0 = 0 м/с
Ep = Ep1+ Ep2 = mgh+mgL = mg(L+h)
Ep = Ek = mv/2=mg(L+h) => v = (2mg(L+h)/(m))^(1/2) = (2* 0,05* 9,8 (0,22 * 0,1 ) / (0,05)) ^(1/2) = 2,5 м/с
Результаты[править]
В ходе создания машины Голдберга были изучены и продемонстрированы многие основные законы теоретической механики. В частности, изучены разделы: статика твёрдого тела, связи и их реакции, моменты сил, кинематика твёрдого тела. Созданная машина Голдберга успешно выполняет поставленную задачу, используя сложную, последовательную цепочку действий.
Видео запуска машины Голдберга.
Литература и ссылки[править]
- Что такое машина Голдберга?
- Машина Голдберга. Что это и зачем?
- Краткий курс теоретической механики
- Машина Голдберга
- Машина Рута Голдберга как объект анализа
- Примеры различных машин Голдберга:
Переворачиватель страниц OK Go - This Too Shall Pass - Rube Goldberg Machine - Official Video World’s largest Rube Goldberg machine lights up Christmas tree Мастерская Голдберга | СПб и Мск | Лекториум The Bet-Losing Machine