Перераспределение энергии между поступательными и вращательными степенями свободы — различия между версиями
Anpolol (обсуждение | вклад) (→Вывод уравнений) |
Anpolol (обсуждение | вклад) (→Вывод уравнений) |
||
| (не показана 31 промежуточная версия этого же участника) | |||
| Строка 1: | Строка 1: | ||
| + | [[ Курсовые_работы_по_ВМДС:_2018-2019 | Курсовые работы 2018-2019 учебного года]] > '''Перераспределение энергии между поступательными и вращательными сстепенями свободы''' <HR> | ||
| + | |||
| + | '''''Курсовой проект по [[Механика дискретных сред|Механике дискретных сред]]''''' | ||
| + | |||
| + | '''Исполнитель:''' [[Андреева Полина]] | ||
| + | |||
| + | '''Группа:''' 43604/1 | ||
| + | |||
| + | '''Семестр:''' осень 2018 | ||
| + | |||
===Постановка задачи=== | ===Постановка задачи=== | ||
| Строка 5: | Строка 15: | ||
===Вывод уравнений=== | ===Вывод уравнений=== | ||
| − | + | Рассматривается система из N тел-точек. Каждое <math>i</math>-ое тело имеет две степени свободы - смещение вдоль вертикальной оси <math>y_{i}</math>, и угол поворота относительно вертикальной оси <math>\phi_{i}</math>. | |
| + | Все тела соединены стержнями, которые описываются уравнением балки Бернулли - Эйлера. | ||
| + | Движение каждого тела - точки описывается уравнениями: | ||
| + | |||
| + | <math> | ||
| + | J \ddot{\phi_{i}} = -M_{i-1}(l) + M_{i}(0) | ||
| + | </math><br /> | ||
| + | <math> | ||
| + | m \ddot{y_{i}} = F_{i-1}(l) - F_{i}(0), | ||
| + | </math><br /> | ||
| + | где <math>J - </math>момент инерции тела-точки. | ||
| + | Моменты и силы находим по определению: | ||
| + | |||
| + | <math> | ||
| + | M = E \cdot J_{b} \cdot y''(x) | ||
| + | </math><br /> | ||
| + | <math> | ||
| + | F = E \cdot J_{b} \cdot y'''(x), | ||
| + | </math><br /> | ||
| + | |||
| + | где <math>E - </math> модуль юнга материала балки, <math>J_{b} - </math> момент инерции сечения балки. | ||
| + | Вид функции <math>y(x)</math>. найдем из уравнения Балки - Бернулли Эйлера: | ||
| + | |||
| + | <math> | ||
| + | E \cdot J_{b} \cdot y^{(4)} = 0 | ||
| + | </math><br /> | ||
| + | |||
| + | получаем: | ||
| + | |||
| + | <math> | ||
| + | y(x) = c_1 \frac{x^3}{6} + c_2 \frac{x^2}{2} + c_3x + c_4 | ||
| + | </math><br /> | ||
| + | <math> | ||
| + | \phi(x) = y'(x) = c_1 \frac{x^2}{2} + c_2x + c_3 | ||
| + | </math><br /> | ||
| + | |||
| + | Для поиска коэффициентов необходимы граничные условия. | ||
| + | Для <math>i - </math>ого тела рассмотрим два участка: балка, соединяющая <math>i - 1</math> и <math>i</math> тела: | ||
| + | |||
| + | <math> | ||
| + | y(0) = y_{i-1} | ||
| + | </math><br /> | ||
| + | <math> | ||
| + | y(l) = y_{i} | ||
| + | </math><br /> | ||
| + | <math> | ||
| + | \phi(0) = \phi_{i-1} | ||
| + | </math><br /> | ||
| + | <math> | ||
| + | \phi(l) = \phi_{i} | ||
| + | </math><br /> | ||
| + | |||
| + | и на участке, соединяющим <math>i</math> и <math> i+1 </math> тела-точки: | ||
| + | |||
| + | <math> | ||
| + | y(0) = y_{i} | ||
| + | </math><br /> | ||
| + | <math> | ||
| + | y(l) = y_{i+1} | ||
| + | </math><br /> | ||
| + | <math> | ||
| + | \phi(0) = \phi_{i} | ||
| + | </math><br /> | ||
| + | <math> | ||
| + | \phi(l) = \phi_{i+1} | ||
| + | </math><br /> | ||
| + | |||
| + | где <math>l - </math>длина балки. | ||
| + | |||
| + | Учитывая граничные условия и все вышеприведенные формулы, находим уравнения движения <math>i - </math>ого тела: | ||
| + | <math> | ||
| + | \ddot{y_{i}} = \frac{EJ_{b}}{m}(\frac{12}{l^3}(y_{i+1}-2y_{i}+y_{i-1}) - \frac{6}{l^2}(\phi_{i+1}-\phi_{i-1})) | ||
| + | </math><br /> | ||
| + | <math> | ||
| + | \ddot{\phi_{i}} = \frac{EJ_{b}}{J}(\frac{6}{l^2}(y_{i+1}-y_{i}) - \frac{2}{l}(\phi_{i+1}+4\phi_{i}+\phi_{i-1})) | ||
| + | </math><br /> | ||
| + | |||
| + | ===Обезразмеривание уравнений движения=== | ||
| + | |||
| + | Перепишем уравнения, полученные в предыдущем пункте, в виде: | ||
| + | |||
| + | <math> | ||
| + | \frac{d^2(\frac{y_{i}}{l})}{d(t\omega_{1})^2} = ((\frac{y_{i+1}}{l}-2\frac{y_{i}}{l}+\frac{y_{i-1}}{l}) - \frac{1}{2}(\phi_{i+1}-\phi_{i-1})) | ||
| + | </math><br /> | ||
| + | <math> | ||
| + | \frac{d^2\phi_{i}}{d(t\omega_{1})^2} = \frac{\omega_{2}^2}{\omega_{1}^2}(3(\frac{y_{i+1}}{l}-\frac{y_{i}}{l}) -(\phi_{i+1}+4\phi_{i}+\phi_{i-1})) | ||
| + | </math><br /> | ||
| + | гд | ||
| + | |||
| + | <math> | ||
| + | \omega_{1}^2 = \frac{12EJ_{b}}{ml^3} | ||
| + | </math><br /> | ||
| + | <math> | ||
| + | \omega_{2}^2 = \frac{2EJ_{b}}{Jl} | ||
| + | </math><br /> | ||
| + | положим равными единицам. | ||
| + | |||
| + | Получили обезразмеренные уравнения: | ||
| + | |||
| + | <math> | ||
| + | \overline{y_{i}}'' = \frac{d^2\overline{y_{i}}}{d(\tau)^2} = ((\overline{y_{i+1}}-2\overline{y_{i}}+\overline{y_{i-1}}) - \frac{1}{2}(\phi_{i+1}-\phi_{i-1})) | ||
| + | </math><br /> | ||
| + | <math> | ||
| + | \phi_{i}'' = \frac{d^2\phi_{i}}{d(\tau)^2} = (3(\overline{y_{i+1}}-\overline{y_{i}}) -(\phi_{i+1}+4\phi_{i}+\phi_{i-1})) | ||
| + | </math><br /> | ||
| + | |||
| + | ===Обезразмеривание энергии=== | ||
| − | === | + | Кинетическая энергия данной системы состоит из суммы кинетической энергии поступательного и вращательного движений: |
| + | |||
| + | <math> | ||
| + | T = \sum_{i=1}^N \frac{m\dot{y_{i}}^2}{2} + \sum_{i=1}^N \frac{J\dot{\phi_{i}}^2}{2} | ||
| + | </math><br /> | ||
| + | |||
| + | Для обезразмеривания перепишем вышеприведенное выражение в виде: | ||
| + | |||
| + | <math> | ||
| + | T = \sum_{i=1}^N \frac{ml^2\omega_{1}^2}{2}\left(\frac{d\frac{y_{i}}{l}}{d(t\omega_{1})}\right)^2 + \sum_{i=1}^N \frac{J\omega_{1}^2}{2}\left(\frac{d\phi}{d(t\omega_{1})}\right)^2 | ||
| + | </math><br /> | ||
| + | |||
| + | Получаем обезразмеренную энергию: | ||
| + | |||
| + | <math> | ||
| + | \overline{T} = \frac{T}{ml^2\omega_{1}^2} = \sum_{i=1}^N \frac{(\overline{y_{i}}')^2}{2} + \sum_{i=1}^N \frac{J}{ml^2}\frac{(\phi')^2}{2} | ||
| + | </math><br /> | ||
| + | |||
| + | Осталось вычислить коэффициент перед обезразмеренной кинетической энергией вращательного движения: <math> \frac{J}{ml^2}</math> | ||
| + | |||
| + | Для этого воспользуемся видом частот <math>\omega_{1}^2</math> и <math>\omega_{2}^2 </math>, полученные в предыдущем пункте и получим, что <math> \frac{J}{ml^2}= \frac{1}{6}</math> | ||
| + | |||
| + | Окончательно, обезраземеренная кинетическая энергия системы примет вид: | ||
| + | |||
| + | <math> | ||
| + | \overline{T} = \sum_{i=1}^N \frac{(\overline{y_{i}}')^2}{2} + \frac{1}{6} \sum_{i=1}^N \frac{(\phi')^2}{2} | ||
| + | </math><br /> | ||
| + | Обозначим обезразмеренную кинетическую энергию вращательного движения | ||
| + | |||
| + | <math> | ||
| + | \overline{T_t} = \frac{1}{6} \sum_{i=1}^N \frac{(\phi')^2}{2} | ||
| + | </math><br /> | ||
| + | |||
| + | а обезразмеренную кинетическую энергию поступательного движения | ||
| + | |||
| + | <math> | ||
| + | \overline{T_p} = \sum_{i=1}^N \frac{(\overline{y_{i}}')^2}{2} | ||
| + | </math><br /> | ||
===Визуализация=== | ===Визуализация=== | ||
| + | Рассмотрим для системы из <math>N= 100</math> частиц и времени <math>\tau = 100</math> три случая: | ||
| + | |||
| + | 1. В начальный момент времени энергия поступательного движения <math> \overline{T_p} = 0</math>, а энергия вращательного движения задается случайным образом <math> \overline{T_t} = 2.04697 </math> | ||
| + | |||
| + | В данном случае перераспределение энергий выглядит следующим образом: | ||
| + | |||
| + | [[File:МДСПОСТУП НОЛЬ3.png|center]] | ||
| + | |||
| + | Средняя по всему времени реализации энергия кинетической энергии поступательного движения равна <math> \overline{T_p} = 0.248106 </math>, а вращательного <math> - \overline{T_t} = 0.774789 </math> | ||
| + | |||
| + | 2. В начальный момент времени энергия вращательного движения <math> \overline{T_t} = 0</math>, а энергия поступательного движения задается случайным образом <math> \overline{T_p} = 11.5927 </math> | ||
| + | |||
| + | В данном случае перераспределение энергий выглядит следующим образом: | ||
| + | |||
| + | [[File:МДСВРАЩ НОЛЬ3.png|center]] | ||
| + | |||
| + | Средняя по всему времени реализации энергия кинетической энергии поступательного движения равна <math> \overline{T_p} = 4.39032 </math>, а вращательного <math> - \overline{T_t} = 1.57495 </math> | ||
| + | |||
| + | 3. В начальный момент времени и энергия вращательного движения и энергия поступательного движения задаются случайным образом <math> \overline{T_p} = 10.8439 </math>, <math> \overline{T_t} = 1.94736 </math> | ||
| + | |||
| + | В данном случае перераспределение энергий выглядит следующим образом: | ||
| + | [[File:МДСРАНДОМ3.png|center]] | ||
| + | |||
| + | Средняя по всему времени реализации энергия кинетической энергии поступательного движения равна <math> \overline{T_p} = 4.39978 </math>, а вращательного <math> - \overline{T_t} = 2.22725 </math> | ||
| + | |||
| + | === Выводы === | ||
| + | В ходе данной работы, можно сделать следующие выводы: | ||
| + | |||
| + | 1. Энергия перераспределяется таким образом, что средние по всему времени реализации работы энергии вращательного и поступательного движения не равны. | ||
| + | |||
| + | 2. При выборе <math> \frac{\omega_{1}^2}{\omega_{2}^2} = 1 </math>: | ||
| + | |||
| + | * в случае, когда начальная энергия вращательного движения равна нулю, отношение средней по всей реализации работы энергии поступательного движения к энергии вращательного движения равна примерно 3 | ||
| + | |||
| + | * в случае, когда начальная энергия поступательного движения равна нулю, отношение средней по всей реализации работы энергии вращательного движения к энергии поступательного движения равна примерно 2.7 | ||
| + | |||
| + | * в случае, когда начальная энергия и вращательного и поступательного движения задаются случайным образом, отношение средней по всей реализации работы энергии поступательного движения к энергии вращательного движения равна примерно 2 | ||
| + | |||
| + | == Ссылки == | ||
| + | |||
| + | *[[Курсовые работы по ВМДС: 2018-2019]] | ||
| + | *[[Введение в механику дискретных сред]] | ||
Текущая версия на 17:14, 25 января 2019
Курсовые работы 2018-2019 учебного года > Перераспределение энергии между поступательными и вращательными сстепенями свободыКурсовой проект по Механике дискретных сред
Исполнитель: Андреева Полина
Группа: 43604/1
Семестр: осень 2018
Содержание
Постановка задачи[править]
Рассмотреть перераспределение энергии между вращательными и поступательными степенями свободы в системе из N тел-точек, соединенных друг с другом балками Бернулли-Эйлера.
Вывод уравнений[править]
Рассматривается система из N тел-точек. Каждое -ое тело имеет две степени свободы - смещение вдоль вертикальной оси , и угол поворота относительно вертикальной оси . Все тела соединены стержнями, которые описываются уравнением балки Бернулли - Эйлера. Движение каждого тела - точки описывается уравнениями:
где момент инерции тела-точки.
Моменты и силы находим по определению:
где модуль юнга материала балки, момент инерции сечения балки. Вид функции . найдем из уравнения Балки - Бернулли Эйлера:
получаем:
Для поиска коэффициентов необходимы граничные условия. Для ого тела рассмотрим два участка: балка, соединяющая и тела:
и на участке, соединяющим и тела-точки:
где длина балки.
Учитывая граничные условия и все вышеприведенные формулы, находим уравнения движения ого тела:
Обезразмеривание уравнений движения[править]
Перепишем уравнения, полученные в предыдущем пункте, в виде:
гд
положим равными единицам.
Получили обезразмеренные уравнения:
Обезразмеривание энергии[править]
Кинетическая энергия данной системы состоит из суммы кинетической энергии поступательного и вращательного движений:
Для обезразмеривания перепишем вышеприведенное выражение в виде:
Получаем обезразмеренную энергию:
Осталось вычислить коэффициент перед обезразмеренной кинетической энергией вращательного движения:
Для этого воспользуемся видом частот и , полученные в предыдущем пункте и получим, что
Окончательно, обезраземеренная кинетическая энергия системы примет вид:
Обозначим обезразмеренную кинетическую энергию вращательного движения
а обезразмеренную кинетическую энергию поступательного движения
Визуализация[править]
Рассмотрим для системы из частиц и времени три случая:
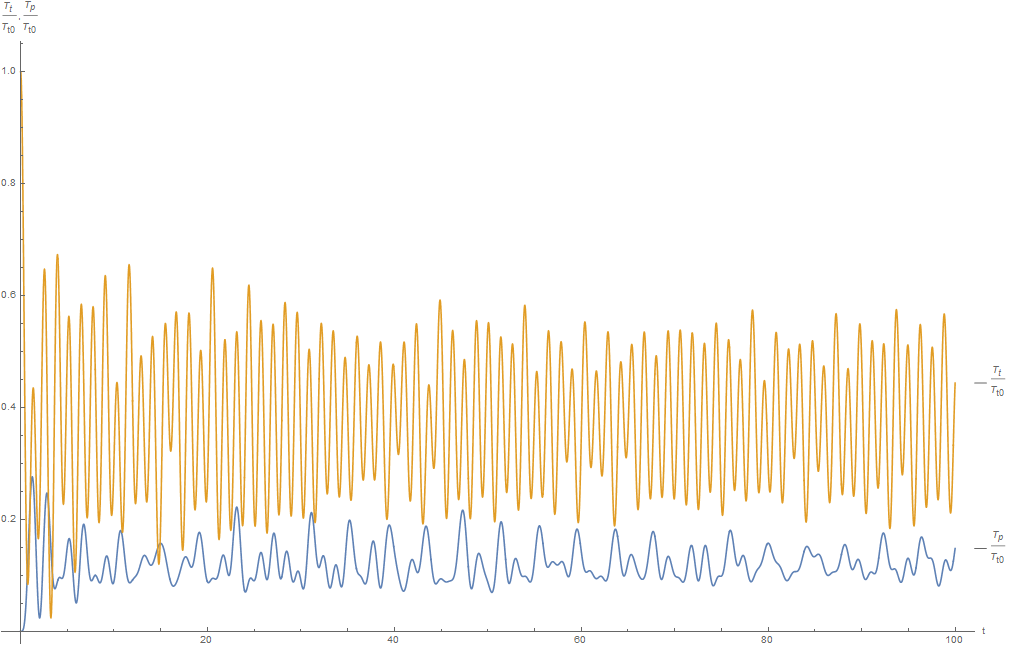
1. В начальный момент времени энергия поступательного движения , а энергия вращательного движения задается случайным образом
В данном случае перераспределение энергий выглядит следующим образом:
Средняя по всему времени реализации энергия кинетической энергии поступательного движения равна , а вращательного
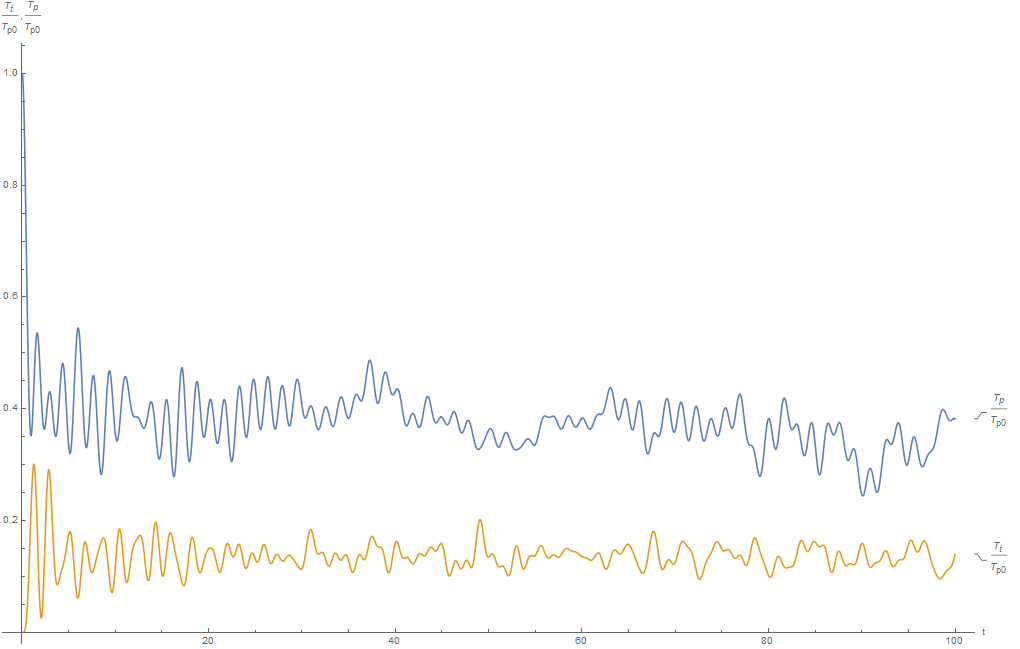
2. В начальный момент времени энергия вращательного движения , а энергия поступательного движения задается случайным образом
В данном случае перераспределение энергий выглядит следующим образом:
Средняя по всему времени реализации энергия кинетической энергии поступательного движения равна , а вращательного
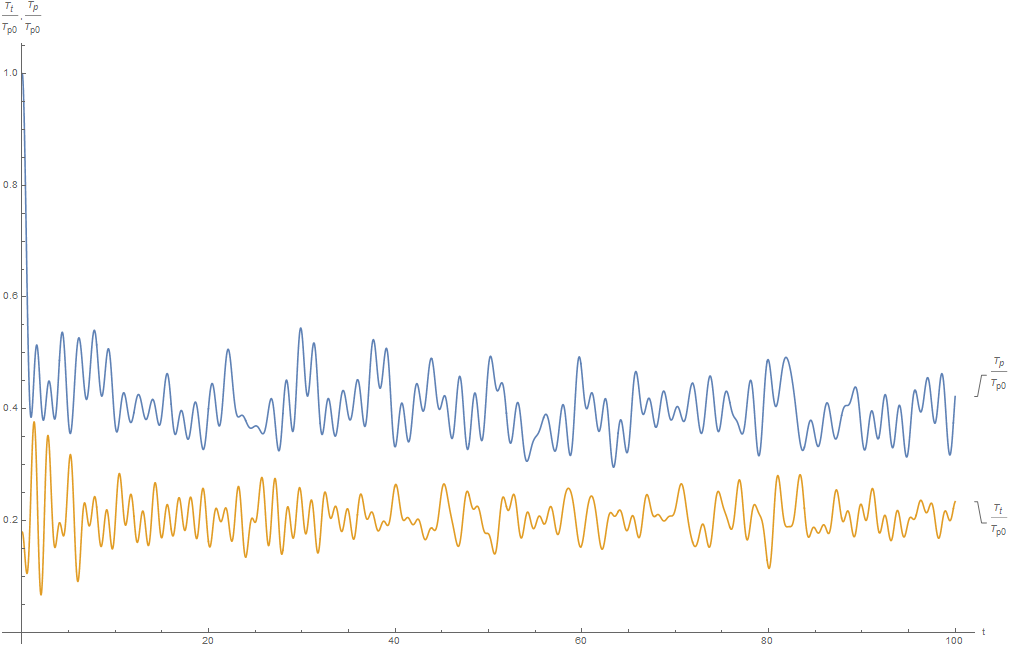
3. В начальный момент времени и энергия вращательного движения и энергия поступательного движения задаются случайным образом ,
В данном случае перераспределение энергий выглядит следующим образом:
Средняя по всему времени реализации энергия кинетической энергии поступательного движения равна , а вращательного
Выводы[править]
В ходе данной работы, можно сделать следующие выводы:
1. Энергия перераспределяется таким образом, что средние по всему времени реализации работы энергии вращательного и поступательного движения не равны.
2. При выборе :
- в случае, когда начальная энергия вращательного движения равна нулю, отношение средней по всей реализации работы энергии поступательного движения к энергии вращательного движения равна примерно 3
- в случае, когда начальная энергия поступательного движения равна нулю, отношение средней по всей реализации работы энергии вращательного движения к энергии поступательного движения равна примерно 2.7
- в случае, когда начальная энергия и вращательного и поступательного движения задаются случайным образом, отношение средней по всей реализации работы энергии поступательного движения к энергии вращательного движения равна примерно 2