Гранецентрированная кубическая решетка — различия между версиями
м |
|||
| (не показаны 4 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
| + | [[ТМ|Кафедра ТМ]] > [[Научный справочник]] > [[Кристаллические решетки]] > '''ГЦК решетка''' <HR> | ||
| + | |||
[[Файл: fcc.png|thumb|]] | [[Файл: fcc.png|thumb|]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <math>\textbf{n}_{1,2,3,4},=\frac{1}{\sqrt{2}}(\pm \textbf{i}\pm \textbf{j}),\quad \textbf{n}_{5,6,7,8},=\frac{1}{\sqrt{2}}(\pm \textbf{j}\pm \textbf{k}),\quad \textbf{n}_{9,10,11,12},=\frac{1}{\sqrt{2}}(\pm \textbf{i}\pm \textbf{k}). | + | ''Сокращенное название:'' ГЦК решетка. |
| − | </math>[[Category: Кристаллические решетки]] | + | |
| + | ''Еnglish:'' FCC (face-centered cubic) lattice. | ||
| + | |||
| + | == Структура решетки == | ||
| + | |||
| + | Атомы расположены в центрах граней и вершинах [[Кубическая кристаллическая решетка|простой кубической решетки]]. Соответствует одной из возможных плотных упаковок шаров в пространстве. Ближайшие друг к другу атомы формируют тетраэдры и октаэдры, полностью заполняющие пространство.<REF>[https://en.wikipedia.org/wiki/Tetrahedral-octahedral_honeycomb Tetrahedral-octahedral honeycomb].</REF> Область пространства, лежащая ближе к данному атому, чем к остальным атомам,<REF>Для простых решеток подобную область называют [https://ru.wikipedia.org/wiki/%D0%AF%D1%87%D0%B5%D0%B9%D0%BA%D0%B0_%D0%92%D0%B8%D0%B3%D0%BD%D0%B5%D1%80%D0%B0_%E2%80%94_%D0%97%D0%B5%D0%B9%D1%82%D1%86%D0%B0 ячейкой Вигнера-Зейтца].</REF> для ГЦК решетки представляет собой [https://ru.wikipedia.org/wiki/%D0%A0%D0%BE%D0%BC%D0%B1%D0%BE%D0%B4%D0%BE%D0%B4%D0%B5%D0%BA%D0%B0%D1%8D%D0%B4%D1%80 ромбододекаэдр]. Атомы, ближайшие к данному, лежат на вершинах [https://ru.wikipedia.org/wiki/%D0%9A%D1%83%D0%B1%D0%BE%D0%BE%D0%BA%D1%82%D0%B0%D1%8D%D0%B4%D1%80 кубооктаэдра]. | ||
| + | |||
| + | == Распространенность в природе == | ||
| + | |||
| + | Этой решеткой обладает ряд металлов (алюминий, золото, медь, серебро, никель, платина и др.), ее образуют при конденсации инертные газы. | ||
| + | |||
| + | == Геометрия решетки == | ||
| + | |||
| + | Орты (единичные векторы) <math>{\bf n}_\alpha</math>, задающие направление от некоторого атома кристаллической решетки к его ближайшим соседям, могут быть представлены в виде: | ||
| + | |||
| + | :<math>\textbf{n}_{1,2,3,4},=\frac{1}{\sqrt{2}}(\pm \textbf{i}\pm \textbf{j}),\quad \textbf{n}_{5,6,7,8},=\frac{1}{\sqrt{2}}(\pm \textbf{j}\pm \textbf{k}),\quad \textbf{n}_{9,10,11,12},=\frac{1}{\sqrt{2}}(\pm \textbf{i}\pm \textbf{k}) | ||
| + | </math>, | ||
| + | |||
| + | где <math>{\bf i},\,{\bf j},\,{\bf k}</math> — орты Декартовой системы координат. | ||
| + | |||
| + | Безразмерные параметры координационного тензора<REF>[[А.М. Кривцов]]. Теоретическая механика. [[Упругие свойства одноатомных и двухатомных кристаллов]]: учеб. пособие. - СПб.: Изд-во Политехн. ун-та, 2009. - 126 c.</REF> | ||
| + | |||
| + | :<math> | ||
| + | \eta=2; \quad | ||
| + | M_\kappa=-1; \quad | ||
| + | M_\mu=1. | ||
| + | </math> | ||
| + | |||
| + | [[Category: Кристаллические решетки]] | ||
| + | |||
| + | == Примечания == | ||
| + | <references> </references> | ||
Текущая версия на 02:41, 30 сентября 2013
Кафедра ТМ > Научный справочник > Кристаллические решетки > ГЦК решеткаСокращенное название: ГЦК решетка.
Еnglish: FCC (face-centered cubic) lattice.
Структура решетки[править]
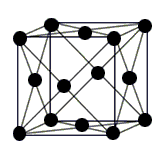
Атомы расположены в центрах граней и вершинах простой кубической решетки. Соответствует одной из возможных плотных упаковок шаров в пространстве. Ближайшие друг к другу атомы формируют тетраэдры и октаэдры, полностью заполняющие пространство.[1] Область пространства, лежащая ближе к данному атому, чем к остальным атомам,[2] для ГЦК решетки представляет собой ромбододекаэдр. Атомы, ближайшие к данному, лежат на вершинах кубооктаэдра.
Распространенность в природе[править]
Этой решеткой обладает ряд металлов (алюминий, золото, медь, серебро, никель, платина и др.), ее образуют при конденсации инертные газы.
Геометрия решетки[править]
Орты (единичные векторы) , задающие направление от некоторого атома кристаллической решетки к его ближайшим соседям, могут быть представлены в виде:
- ,
где — орты Декартовой системы координат.
Безразмерные параметры координационного тензора[3]
Примечания[править]
- ↑ Tetrahedral-octahedral honeycomb.
- ↑ Для простых решеток подобную область называют ячейкой Вигнера-Зейтца.
- ↑ А.М. Кривцов. Теоретическая механика. Упругие свойства одноатомных и двухатомных кристаллов: учеб. пособие. - СПб.: Изд-во Политехн. ун-та, 2009. - 126 c.