Колебание системы с двумя степенями свободы — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
(→Решение) |
|||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 2: | Строка 2: | ||
== Формулировка задачи == | == Формулировка задачи == | ||
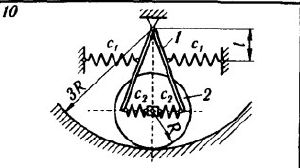
| − | Определить частоты малых свободных колебаний и формы главных колебаний системы с двумя степенями свободы, пренебрегая силами сопротивления, массами пружин и моментами инерции скручиваемых валов. | + | [[File:NWc9RylEY1M (1).jpg|мини|300 px]] |
| + | Определить частоты малых свободных колебаний и формы главных колебаний системы с двумя степенями свободы, пренебрегая силами сопротивления, массами пружин и моментами инерции скручиваемых валов. | ||
==Решение== | ==Решение== | ||
| − | [http://mech.spbstu.ru/File: | + | [http://mech.spbstu.ru/File:Kursach.docx Скачать курсовую работу] |
{{#widget:Iframe |url= http://tm.spbstu.ru/htmlets/SakevichTS/K2.html |width=1250 |height=850}} | {{#widget:Iframe |url= http://tm.spbstu.ru/htmlets/SakevichTS/K2.html |width=1250 |height=850}} | ||
Текущая версия на 11:01, 31 мая 2018
Выполнила Сакевич Татьяна
Формулировка задачи[править]
Определить частоты малых свободных колебаний и формы главных колебаний системы с двумя степенями свободы, пренебрегая силами сопротивления, массами пружин и моментами инерции скручиваемых валов.
Решение[править]
Текст программы на языке JavaScript:
1 window.addEventListener("load", program_code, false) ;
2 function program_code(){
3 var ctx=canvas_example.getContext("2d");
4 var w=canvas_example.width;
5 var l=canvas_example.height;
6 ctx.strokeRect(0,0,w,l);
7 function draw2() //оси
8 {
9 Y0=250;
10 X0=160;
11 ctx.strokeStyle = 'lightgrey';
12 ctx.beginPath();
13 ctx.moveTo(0, Y0);
14 ctx.lineTo(canvas_example.width, Y0);
15 ctx.moveTo(X0, 0);
16 ctx.lineTo(X0, canvas_example.height);
17 ctx.stroke();
18 ctx.fillStyle = 'black';
19 ctx.font = "20px Times";
20 ctx.fillText("0",163, 330);
21 ctx.font = "italic 20px Times";
22 ctx.fillText("t",1150,330);
23 ctx.fillText("x",150, 20);
24 }
25 draw2();
26 function count()
27 {
28 var m1 = parseFloat(input_m1.value);
29 var m2 = parseFloat(input_m2.value);
30 var R= parseFloat(input_R.value);
31 var l= parseFloat(input_l.value);
32 var q0=parseFloat(input_q0.value);
33 var v0= parseFloat(input_v0.value);
34 var ix= parseFloat(input_ix.value);
35 var c1= parseFloat(input_c1.value);
36 var c2= parseFloat(input_c2.value);
37 var t= parseFloat(input_t.value)
38
39 var a1=0.75*m2;
40 var a2=m1*ix*ix;
41
42 var Q=9.8*m1*l+c1*l*l+4*c2*R*R;
43 var P=2.45*m2/R+c2;
44 var G=-4*c2*R;
45
46 var k1=(a1*P+a2*Q +Math.sqrt((a1*P+a2*Q)*(a1*P+a2*Q)-4*a1*a2*(Q*P-G*G)))/(2*a1*a2);
47 var k2=(a1*P+a2*Q -Math.sqrt((a1*P+a2*Q)*(a1*P+a2*Q)-4*a1*a2*(Q*P-G*G)))/(2*a1*a2);
48
49 var A1=q0;
50 var A2=v0/k1
51
52 dt=0.02;
53 q=[];
54 q[0]=q0;
55 n=t/dt;
56 var T=0;
57 for (var i=0; i<n; i++) {
58 T+=dt;
59
60 q[i]=10*(A1*Math.sin(k1*T)+A2*Math.sin(k2*T));
61
62 }
63
64 }
65 function draw()
66 {
67 ctx.strokeRect(0,0,w,l);
68 draw2();
69 ctx.strokeStyle = 'black';
70 ctx.beginPath()
71 for (var i=0; i<n; i++) {
72 ctx.lineTo((i/(n-1)*w)+X0,(l-q[i]*l)/50+Y0);
73 ctx.stroke();
74 }
75 }
76
77 button_alert.onclick=function(){
78 ctx.clearRect(0,0,w,l);
79 count();
80 draw();
81 }
82 }