Система блоков (38.31) — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎Реализация при помощи JS)
 
(не показана 1 промежуточная версия 1 участника)
Строка 4: Строка 4:
 
== Реализация при помощи JS ==
 
== Реализация при помощи JS ==
 
{{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Drepin/mesherskiy/38.31.html|width=940 |height=400 |border=0 }}
 
{{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Drepin/mesherskiy/38.31.html|width=940 |height=400 |border=0 }}
−
Программа: [[Медиа:Mesherskiy3831.zip|Скачать]]
+
Программа: [http://tm.spbstu.ru/htmlets/Drepin/mesherskiy/Mesherskiy3831.zip Скачать]
  
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible mw-collapsed">
Строка 264: Строка 264:
 
// Align top-left
 
// Align top-left
 
stats.domElement.style.position = 'absolute';
 
stats.domElement.style.position = 'absolute';
−
stats.domElement.style.left = '0px';
+
stats.domElement.style.right = '0px';
 
stats.domElement.style.top = '0px';
 
stats.domElement.style.top = '0px';
 
document.getElementById("Stats-output").appendChild(stats.domElement);
 
document.getElementById("Stats-output").appendChild(stats.domElement);

Текущая версия на 15:37, 15 декабря 2017

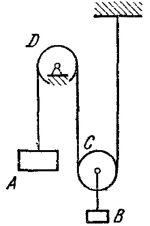
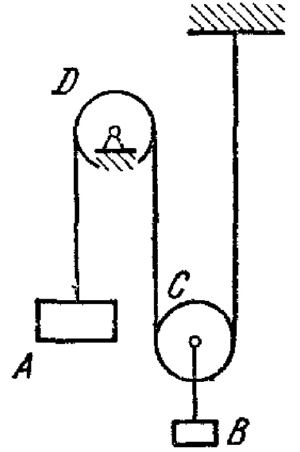
Задача 38.31 из сборника задач Мещерского Задача: С помощью языка программирования JavaScript смоделировать систему блоков с грузом. Построить график зависимости скорости от прошедшего времени.

Система блоков с грузами (A - груз 1, B - груз 2, C - подвижный блок, D - неподвижный блок.)

Реализация при помощи JS[править]

Программа: Скачать

Текст программы на языке JavaScript:

Файл "twoblocks.js" 

  1 function init() {
  2 	const g=9.8;
  3 	var ctxp = canvas_plot.getContext("2d");
  4 	var wp = canvas_plot.width;
  5 	var hp = canvas_plot.height;
  6 	var Yt = [];
  7 	var M1=25;
  8 	var M2=1;
  9 	var M3=1;
 10 	var Y=0;
 11 	var X=0;
 12 	var line;
 13 	var t=0;
 14 	var angle = 0;
 15 	var moving = false;
 16 	var stats = initStats();
 17 	// create a scene, that will hold all our elements such as objects, cameras and lights.
 18 	var scene = new THREE.Scene();
 19 	var clock = new THREE.Clock();
 20 	// create a camera, which defines where we're looking at.
 21 	var camera = new THREE.PerspectiveCamera(45, window.innerWidth / window.innerHeight, 0.1, 1000);
 22 		camera.position.x = -15;
 23 		camera.position.y = 45;
 24 		camera.position.z = 50;
 25 	// call the render function
 26 	// create a render and set the size
 27 	var webGLRenderer = new THREE.WebGLRenderer();
 28 		webGLRenderer.setClearColor(new THREE.Color(0xaaabfe, 1.0));
 29 		webGLRenderer.setSize(window.innerWidth, window.innerHeight);
 30 		webGLRenderer.shadowMapEnabled = true;
 31 	// create the ground plane
 32 	var textureGrass = THREE.ImageUtils.loadTexture("grasslight-big.jpg");
 33 		textureGrass.wrapS = THREE.RepeatWrapping;
 34         textureGrass.wrapT = THREE.RepeatWrapping;
 35         textureGrass.repeat.set(4, 4);
 36     var planeGeometry = new THREE.PlaneGeometry(1500, 400, 20, 20);
 37     var planeMaterial = new THREE.MeshLambertMaterial({map: textureGrass});
 38     var plane0 = new THREE.Mesh(planeGeometry, planeMaterial);
 39         plane0.receiveShadow = true;
 40         plane0.rotation.x = -0.5 * Math.PI;
 41         plane0.position.x = -25;
 42         plane0.position.y = -50;
 43         plane0.position.z = 0;
 44         scene.add(plane0);	
 45 	var cylinder1 = createMesh(new THREE.CylinderGeometry(5, 5, 2, 18), "plaster.jpg");
 46 		cylinder1.rotation.x = 1.57;
 47 		cylinder1.position.x = -15;
 48 		cylinder1.position.y = Y/2+7;
 49 	var cylinder2 = createMesh(new THREE.CylinderGeometry(5, 5, 2, 18), "plaster.jpg");
 50 		cylinder2.rotation.x = 1.57;
 51 		cylinder2.position.x = 0;
 52 		cylinder2.position.y = 18;
 53 	var plane1 = createMesh(new THREE.PlaneGeometry(10, 15, 4, 4), "cat.jpg");
 54 		plane1.rotation.x = -1.57;
 55 		plane1.position.x = -30;
 56 		plane1.position.y = 25;
 57 	var plane2 = createMesh(new THREE.PlaneGeometry(10, 15, 4, 4), "dog.jpg");
 58 		plane2.rotation.x = -1.57;
 59 		plane2.position.x = 0;
 60 		plane2.position.y = 26;	
 61 	var box1 = createMesh(new THREE.BoxGeometry(8, 6, 8), "brick-wall.jpg");
 62 		box1.position.x = 5;
 63 		box1.position.y = -Y;
 64 	var box2 = createMesh(new THREE.BoxGeometry(8, 9, 8), "darker_wood.jpg");
 65 		box2.position.x = -15;
 66 		box2.position.y = Y/2-11;
 67 		box2.position.z = 0;
 68 	var box3 = createMesh(new THREE.BoxGeometry(3, 8, 4), "metal-rust.jpg");
 69 		box3.position.x = -15;
 70 		box3.position.y = Y/2+4;
 71 		box3.position.z = 0;
 72 	var box4 = createMesh(new THREE.BoxGeometry(1, 4, 1), "metal-rust.jpg");
 73 		box4.position.x = -14;
 74 		box4.position.y = Y/2-2;
 75 		box4.position.z = 0;
 76 	var box5 = createMesh(new THREE.BoxGeometry(2, 1, 1), "metal-rust.jpg");
 77 		box5.position.x = -15;
 78 		box5.position.y = Y/2-4;
 79 		box5.position.z = 0;
 80 	var box6 = createMesh(new THREE.BoxGeometry(1, 1, 1), "metal-rust.jpg");
 81 		box6.position.x = -16;
 82 		box6.position.y = Y/2-3;
 83 		box6.position.z = 0;
 84 	var box7 = createMesh(new THREE.BoxGeometry(2, 8, 4), "metal-rust.jpg");
 85 		box7.position.x = 0;
 86 		box7.position.y = 21.99;	
 87 	var points = [];
 88 		points.push({x: -30, y: 25, z: 0});
 89 		points.push({x: -20, y: Y/2+7, z: 0});
 90 		points.push({x: -10, y: Y/2+7, z: 0});
 91 		points.push({x: -5, y: 18, z: 0});
 92 		points.push({x: 5, y: 18, z: 0});
 93 		points.push({x: 5, y: -Y, z: 0});								
 94 	var lines = new THREE.Geometry();
 95 	var colors = [];
 96 	var i = 0;
 97 	points.forEach(function (e) {
 98 		lines.vertices.push(new THREE.Vector3(e.x, e.y, e.z));
 99 		colors[i] = new THREE.Color(0x5757bb);
100 		i++;
101 	});
102 	lines.colors = colors;
103 	var materialLine = new THREE.LineBasicMaterial({
104 		opacity: 1.0,
105 		linewidth: 1,
106 		vertexColors: THREE.VertexColors
107 	});
108 
109 	line = new THREE.Line(lines, materialLine);
110 	line.position.set(0, 0, 0);
111 	
112 	// add everything to the scene
113 	scene.add(plane1, plane2, cylinder1, cylinder2, box1, box2, box3, box4,box5,box6,box7);
114 	
115         var spotLight = new THREE.SpotLight(0xffffff);
116         spotLight.position.set(-40, 60, -10);
117         spotLight.castShadow = true;
118         scene.add( spotLight );
119         scene.add(new THREE.AmbientLight("#999999"));
120 
121 		
122 	// add the output of the renderer to the html element
123 	webGLRenderer.domElement.style.width='100%';
124 	document.getElementById("WebGL-output").appendChild(webGLRenderer.domElement);
125 	var controls = new function () {
126 			this.bricks = 25;
127 			this.blocks = 1;
128 			this.wood = 1;
129 			this.spin = false;
130             this.redraw = function () {
131 				M1=controls.bricks;
132 				M2=controls.blocks;
133 				M3=controls.wood;
134 				moving=controls.spin;
135             };
136         };
137 
138         var gui = new dat.GUI();
139 		gui.add(controls, 'bricks', 1, 50).onChange(controls.redraw);
140 		gui.add(controls, 'blocks', 1, 50).onChange(controls.redraw);
141 		gui.add(controls, 'wood', 1, 50).onChange(controls.redraw);
142         gui.add(controls, 'spin', 0, 1).onChange(controls.redraw);
143 		gui.domElement.style.position = 'absolute';
144         gui.domElement.style.left = '0px';
145 		document.getElementsByClassName('dg main a')[0].style.height= '400px' ;
146 		var trackballControls = new THREE.TrackballControls(camera, webGLRenderer.domElement);
147 		trackballControls.rotateSpeed = 1.0;
148         trackballControls.zoomSpeed = 1.0;
149         trackballControls.panSpeed = 1.0;
150         trackballControls.staticMoving = true;
151         render();
152 	function createMesh(geom, imageFile) {
153 		var texture = THREE.ImageUtils.loadTexture(imageFile);
154 		var mat = new THREE.MeshPhongMaterial();
155 		if(geom.type=='PlaneGeometry') mat.side = THREE.DoubleSide;
156 		mat.map = texture;
157 		var mesh = new THREE.Mesh(geom, mat);
158 		return mesh;
159 	}
160 	function physics(delta) {
161 		scene.remove(line);
162 		t+=1/60;
163 		if((2*M1-M2-M3)!=0)Y=t*t*(2*g*(2*M1-M2-M3))/(8*M1+2*M2+7*M3);
164 		if(Y>0) X=(-1)*Y*((cylinder1.position.x-2.5-plane1.position.x)/Math.sqrt(Math.pow((plane1.position.x-cylinder1.position.x-2.5),2)+Math.pow((plane1.position.y-Y/2),2)));
165 		
166 		cylinder2.rotation.y =-Y/5;
167 		cylinder1.rotation.y =Y/5;
168 		cylinder1.position.y = Y/2+7
169 		box1.position.y = -Y;
170 		box2.position.y = Y/2-11;
171 		box3.position.y = Y/2+4;
172 		box4.position.y = Y/2-2;
173 		box5.position.y = Y/2-4;
174 		box6.position.y = Y/2-3;
175 		
176 		cylinder1.position.x = X-15;
177 		box2.position.x = X-15;
178 		box3.position.x = X-15;
179 		box4.position.x = X-14;
180 		box5.position.x = X-15;
181 		box6.position.x = X-16;
182 	
183 	var points = new Array(6);
184 		points.push({x: -30, y: 25, z: 0});
185 		points.push({x: X-20, y: Y/2+7, z: 0});
186 		points.push({x: X-10, y: Y/2+7, z: 0});
187 		points.push({x: -4, y: 20, z: 0});
188 		points.push({x: 5, y: 18, z: 0});
189 		points.push({x: 5, y: -Y, z: 0});								
190 	var lines = new THREE.Geometry();
191 	var colors = [];
192 	var i = 0;
193 	points.forEach(function (e) {
194 		lines.vertices.push(new THREE.Vector3(e.x, e.y, e.z));
195 		colors[i] = new THREE.Color(0x5757bb);
196 		i++;
197 	});
198 	lines.colors = colors;
199 	var materialLine = new THREE.LineBasicMaterial({
200 		opacity: 1.0,
201 		linewidth: 1,
202 		vertexColors: THREE.VertexColors
203 	});
204 	line = new THREE.Line(lines, materialLine);
205 	line.position.set(0, 0, 0);
206 	scene.add(line);
207 	
208 	ctxp.clearRect(0, 0, wp, hp);
209 	ctxp.strokeRect(0, 0, wp, hp);
210 		y = 2*Y^(1/2)
211 		Yt.push(y);
212 		if (Yt.length > 500) Yt.shift();
213 		var N = Yt.length;
214 		var max=Yt[0];
215 		var min=Yt[0];
216 		for (var i = 1; i < N; i++) {
217 			if (Yt[i] > max) max = Yt[i];
218 			if (Yt[i] < min) min = Yt[i];
219 		}	
220 		ctxp.beginPath();
221 		for (var i = 0; i < N; i++) {
222 			var xp = i/(N-1)*wp;
223 			var yp = hp-(Yt[i]-min)/(max - min)*hp;
224 			if (i == 0) {
225 				ctxp.moveTo(xp, yp);
226 			} else {
227 				ctxp.lineTo(xp, yp);
228 			}
229 		}
230 	ctxp.stroke();
231 		if (moving){
232 			angle += 1*delta ; // приращение угла
233 			camera.position.x = Math.cos(angle) * 70;
234 			camera.position.z = Math.sin(angle) * 70;
235 		}
236 	}
237 	
238 	function render() {
239 		stats.update();
240 		var delta = clock.getDelta();
241         trackballControls.update(delta);
242 		webGLRenderer.render(scene, camera);
243 		if(Y/2+15<=25) physics(delta)
244 		else{
245 			Y=0;
246 			t=0;
247 		}	
248 		requestAnimationFrame(render);
249 	}
250 	function initStats() {
251 		var stats = new Stats();
252 		stats.setMode(0); // 0: fps, 1: ms
253 		// Align top-left
254 		stats.domElement.style.position = 'absolute';
255 		stats.domElement.style.right = '0px';
256 		stats.domElement.style.top = '0px';
257 		document.getElementById("Stats-output").appendChild(stats.domElement);
258 		return stats;
259     }
260 }
261 window.onload = init;

Используемые библиотеки[править]

  • three.js
  • stats.js
  • dat.gui.js
  • TrackballControls.js

Возможности программы[править]

  • Изменение положения камеры и включение движения вокруг системы
  • Интерактивное представление скорости в виде графика
  • Изменение масс грузов

Решение частного случая[править]

Условия задачи:

Картинка к задаче.

Груз [math]A[/math] массы [math]M_{1}[/math], опускаясь вниз, при помощи троса, перекинутого через неподвижный блок [math]D[/math], поднимает вверх груз [math]B[/math] массы [math]M_{2}[/math], прикрепленный к оси подвижного блока [math]C[/math]. Блоки [math]C[/math] и [math]D[/math] считать однородными сплошными дисками массы [math]M_{3}[/math] каждый. Определить скорость груза [math]A[/math] в момент, когда он опустится на высоту [math]h[/math]. Массой троса, проскальзыванием по ободам блоков и силами сопротивления пренебречь. В начальный момент система находилась в покое.

Решение: В исходной задаче требуется получить зависимость скорости от координаты. Мы же помимо этого хотим получить уравнение движения [math]h(t)[/math].

В основе решения лежит теорема об изменении кинетической энергии материальной системы: [math]{ \Delta}Т=\sum\limits_{i = 1}^n A_{i}[/math] Изменение кинетической энергии системы - энергия, которую система обрела в конечный момент времени, тогда: [math]{ \Delta}Т=T_{h}=\frac{M_{1}*V_{1}^2}{2}+\frac{I_{D}*ω_{D}^2}{2}+\frac{M_{3}*V^2}{2*4}+\frac{I_{C}*ω_{C}^2}{2}+\frac{M_{2}*V^2}{2*4}[/math] [math]{ \Delta}Т=\frac{M_{1}*V_{1}^2}{2}+\frac{M_{3}*V^2}{4}+\frac{3M_{3}*V^2}{16}+\frac{M_{2}*V^2}{8}=\frac{8M_{1}+2M_{1}+7M_{3}}{16}*V_{1}^2 [/math]

Суммарная работа сил тяжести равна:

[math]A=A_{A}+A_{B}+A_{C}+A_{D}=M_{1}gh+0-(M_{3}+M_{2})g\frac{h}{2}=\frac{1}{2}gh(2M_{1}-M_{2}-M_{3})[/math]

Получаем:

[math]\frac{8M_{1}+2M_{1}+7M_{3}}{16}*V_{1}^2=\frac{1}{2}gh(2M_{1}-M_{2}-M_{3})[/math], откуда

[math]V=2 \sqrt{2gh \frac{2M_{1}-M_{2}-M_{3}}{8M_{1}+2M_{1}+7M_{3}}}[/math].

Если вспомнить, что [math]V=\dot{h}[/math], то [math]\dot{h}=2 \sqrt{2gh \frac{2M_{1}-M_{2}-M_{3}}{8M_{1}+2M_{1}+7M_{3}}}[/math], интегрируя, получаем:

[math]\sqrt{h}=\sqrt{2g \frac{2M_{1}-M_{2}-M_{3}}{8M_{1}+2M_{1}+7M_{3}}}t[/math],

[math]h=\frac{2g(2M_{1}-M_{2}-M_{3})}{8M_{1}+2M_{1}+7M_{3}}t^2[/math].

См. также[править]

Источник — «http://tm.spbstu.ru/?title=Система_блоков_(38.31)&oldid=49030»