Управление нелинейными волновыми процессами в нелинейных механических системах — различия между версиями
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 43: | Строка 43: | ||
[[File:fig5-1.png|600px|Пример работы управления]] | [[File:fig5-1.png|600px|Пример работы управления]] | ||
| + | |||
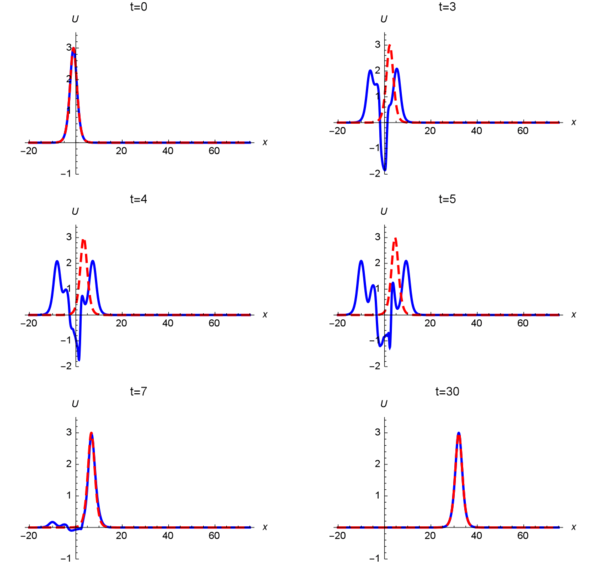
Пример работы управления для дисперсионного уравнения синус-Гордона. Красным цветом -- целевая функция, синим -- численное решение в разные моменты времени | Пример работы управления для дисперсионного уравнения синус-Гордона. Красным цветом -- целевая функция, синим -- численное решение в разные моменты времени | ||
| + | |||
| + | ==Результаты== | ||
| + | |||
| + | Результаты проделанной работы условно можно разделить на математические и физические. | ||
| + | |||
| + | Математические результаты. | ||
| + | |||
| + | Успешно разработан алгоритм управления нелинейными волнами на осно ве метода скоростного градиента. Алгоритм был протестирован на одиночных уравнениях трех типов: уравнении синус-Гордона, двойного уравнения синус Гордона и дисперсионного уравнения синус-Гордона; а также на системе связанных уравнений. В качестве целевых функций управления выбирались не только точные решения в виде солитонов, но и локализованные волны достаточно произвольной формы. Для связанных уравнений средствами удалось восстановить вид точного решения при несоответствии положений волн, отвечающих разным уравнениям, в начальный момент времени. | ||
| + | |||
| + | Физические результаты | ||
| + | |||
| + | Успешно была поставлена механическая задача, а именно задача о плоском упругом слое, нижняя граница которого погружена в морозный грунт, а на верхней границе которого задана произвольная нагрузка. Построено асимптотическое решение поставленной задачи и, таким образом, выведено модельное уравнение для слабо-поперечных волн смещения. Показано, что выбирая нагрузку на верхней границе слоя определенным образом, модельное уравнение принимает вид уравнения синус-Гордона с управлением, и, следовательно, в рассмотренном слое можно осуществлять управление слабо-поперечными волнами смещения. Более того, поставленная задача была рассмотрена в обобщенном случае, в котором также возникает возможность управления волнами. | ||
| + | |||
| + | Таким образом, работа выполнена успешно, выполнены все поставленные цели. Получены результаты, которые могут найти применение как в области физики, так и в области математики. | ||
==Успехи и поддержка== | ==Успехи и поддержка== | ||
Основные результаты: | Основные результаты: | ||
| − | + | * Написано и опубликовано две статьи в журналах IOPScience и Elsevier | |
| − | + | * Доклад на конференции APM-2016 <<Generation of desired nonlinear wave by feedback control>> | |
Работа выполнялась в рамках проекта Российского Научного Фонда 14-29-00142. | Работа выполнялась в рамках проекта Российского Научного Фонда 14-29-00142. | ||
| − | == | + | ==Подробнее== |
| − | + | Подробнее ознакомиться с работой можно прочитав её [[:File:superthesis.pdf|полный текст]], или посмотрев [[:File:presentation2.pdf|презентацию работы]] | |
Текущая версия на 21:27, 29 июня 2017
МАГИСТЕРСКАЯ ДИССЕРТАЦИЯ
Автор работы: Антонов И.Д.
Научный руководитель: д.ф-м.н., профессор А.В. Порубов
Содержание
Введение[править]
В последнее время в разных областях науки наблюдается рост интереса к изучению динамики нелинейных волн. Что же такое нелинейные волны? Нелинейность противопоставляется линейности, то есть подразумевается, что нелинейные волны должны обладать рядом определяющих их свойств, не присущих линейным волнам.
С физической точки зрения, когда говорится о нелинейности, подчеркиваются физические свойства нелинейных волн. Так, волны достаточно малой амплитуды, то есть линейные волны, при распространении в среде не искажаются и не взаимодействуют друг с другом. В то же время волны большей амплитуды — нелинейные — обладают другими свойствами: скорость их начинает зависеть от амплитуды, а также между волнами может осуществляться взаимодействие. Подчеркивается, что для линейных волн, в отличие от нелинейных, выполняется принцип суперпозиции.
С математической же точки зрения, когда говорится о нелинейности, подчеркиваются свойства нелинейных дифференциальных уравнений, которыми описываются процессы в рассматриваемых динамических системах. Для линейных дифференциальных уравнений разработаны и хорошо изучены методы получения их решения. С другой стороны, для нелинейных уравнений нет общего метода их поиска. Получение точных решений нелинейных дифференциальных уравнений представляет собой более трудную и творческую задачу.
Одно из самых известных и изучаемых нелинейных уравнений, среди точных решений которого выделяются уединенные локализованные нелинейные волны-солитоны, — уравнение синус-Гордона. Существует простая механическая интерпретация уравнения синус-Гордона — модель Скотта — механическая система, представляющая из себя маятниковую решетку, в которой распространяются крутильные волны. Теоретически такую систему можно использовать для демонстрации солитонных решений уравнения синус-Гордона. Математически для этого необходимо, чтобы профиль формы и скорости волны в начальный момент времени был задан в виде одного из точных решений уравнения синус-Гордона. На практике точно реализовать такую ситуацию довольно сложно и, соответственно, сложно получить и поддерживать в среде солитон желаемой формы и скорости. При этом поддержание волны в виде солитона представляет собой серьезный научный интерес, так как солитоны могут переносить довольно большую энергию, способную разрушать материал, а так же передавать информацию на большие расстояния. Возникает вопрос: можно ли каким-нибудь способом восстанавливать форму волны и поддерживать в виде солитона для механических структур, описываемых нелинейными уравнениями, такими как уравнение синус-Гордона?
В этих целях могут применяться методы теории управления. Данная работа посвящена изучению и разработке современных методов управления локализованными нелинейными волнами в механических системах.
Первая часть работы[править]
В первой части работы описывается алгоритм распределенного управления волнами в механической среде, поведение которых описывается уравнениями, подобными уравнению синус-Гордона. Для подобного уравнения уже было показано в предыдущих работах, что распределенное управление можно успешно применять для поддержания локализованных волн в случае, если начальные условия не соответствуют точному решению уравнения. Однако в этих работах поддерживаемые управлением волны задавались в виде точных решений уравнения синус-Гордона. К тому же, алгоритм управления тестировался на математической модели, не привязанной к конкретной физической задаче. Одной из целей данной работы был поиск механической задачи, решение которой описывается модельными уравнениями, схожими с уравнением синус-Гордона. Помимо этого, было показано, что в качестве цели управления необязательно должен выбираться солитон, являющийся точным решением уравнения синус Гордона.
Рассмотренные уравнения:
Уравнение синус-Гордона с управлением:
Двойное уравнение синус-Гордона с управлением:
Дисперсионное уравнение синус-Гордона с управлением:
Вторая часть работы[править]
Вторая часть работы посвящена исследованию распределенного управления связанными нелинейными волнами движущихся дефектов в двух атомных кристаллах. В данном случае распространение связанной локализованной волны может быть нарушено, например, неточным соответствием положений начальных форм каждой из волн. Алгоритм управления в таком случае может быть применен для достижения и поддержания обеими волна ми форм точного решения связанной системы уравнений. В частности, алгоритм может устранить осцилляции и другие дефекты в профилях распространяющихся волн, вызванных несоответствием положений максимумов связанных волн в момент генерации. Исследовался случай введения управления в одно из связанных уравнений.
Пример работы управления для дисперсионного уравнения синус-Гордона. Красным цветом -- целевая функция, синим -- численное решение в разные моменты времени
Результаты[править]
Результаты проделанной работы условно можно разделить на математические и физические.
Математические результаты.
Успешно разработан алгоритм управления нелинейными волнами на осно ве метода скоростного градиента. Алгоритм был протестирован на одиночных уравнениях трех типов: уравнении синус-Гордона, двойного уравнения синус Гордона и дисперсионного уравнения синус-Гордона; а также на системе связанных уравнений. В качестве целевых функций управления выбирались не только точные решения в виде солитонов, но и локализованные волны достаточно произвольной формы. Для связанных уравнений средствами удалось восстановить вид точного решения при несоответствии положений волн, отвечающих разным уравнениям, в начальный момент времени.
Физические результаты
Успешно была поставлена механическая задача, а именно задача о плоском упругом слое, нижняя граница которого погружена в морозный грунт, а на верхней границе которого задана произвольная нагрузка. Построено асимптотическое решение поставленной задачи и, таким образом, выведено модельное уравнение для слабо-поперечных волн смещения. Показано, что выбирая нагрузку на верхней границе слоя определенным образом, модельное уравнение принимает вид уравнения синус-Гордона с управлением, и, следовательно, в рассмотренном слое можно осуществлять управление слабо-поперечными волнами смещения. Более того, поставленная задача была рассмотрена в обобщенном случае, в котором также возникает возможность управления волнами.
Таким образом, работа выполнена успешно, выполнены все поставленные цели. Получены результаты, которые могут найти применение как в области физики, так и в области математики.
Успехи и поддержка[править]
Основные результаты:
- Написано и опубликовано две статьи в журналах IOPScience и Elsevier
- Доклад на конференции APM-2016 <<Generation of desired nonlinear wave by feedback control>>
Работа выполнялась в рамках проекта Российского Научного Фонда 14-29-00142.
Подробнее[править]
Подробнее ознакомиться с работой можно прочитав её полный текст, или посмотрев презентацию работы