Метод вейвлет-преобразований для исследований биомедицинских процессов — различия между версиями
Foten (обсуждение | вклад) |
(→Резуьтаты) |
||
| (не показано 11 промежуточных версий 1 участника) | |||
| Строка 25: | Строка 25: | ||
Вейвлет-преобразование отображает исходный сигнал на плоскость непрерывно изменяющихся аргументов – частоты <math>\nu</math> и времени <math>t</math>. | Вейвлет-преобразование отображает исходный сигнал на плоскость непрерывно изменяющихся аргументов – частоты <math>\nu</math> и времени <math>t</math>. | ||
==Сравнение Фурье и вейвлет-преборазования== | ==Сравнение Фурье и вейвлет-преборазования== | ||
| + | Для того, чтобы увидеть все преимущества вейвлет-преобразования в сравнении с преобразованием Фурье, рассмотрим тестовый сигнал: | ||
| + | |||
| + | :<math> z(t) = | ||
| + | \begin{cases} | ||
| + | \cos 2 \pi f_1 t &\text{ $ 0 \leqslant t < 1 $}\\ | ||
| + | \cos 2 \pi f_2 t &\text{ $ 1 \leqslant t < 2 $}\\ | ||
| + | 0 &\text{ $ t < 0 , t > 2 $} | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | Для мощности Фурье и вейвлет спектров имеем следующие графики: | ||
| + | |||
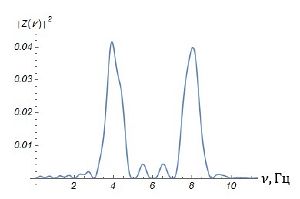
| + | [[File:Feriespect.jpg|thumb|Рис.1. Мощность Фурье спектра]] | ||
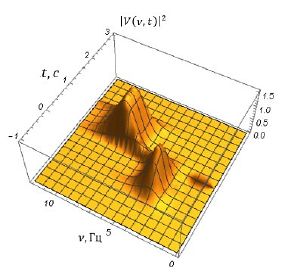
| + | [[File:Wevletspec.jpg|thumb|Рис.2. Мощность Вейвлет спектра]] | ||
| + | |||
| + | |||
| + | Только вейвлет-преобразование выявило момент возникновения каждой частоты и процесс перехода колебаний с одной частотой в колебания другой частоты. | ||
| + | Преимущество вейвлет-преобразования состоит в том, что фиксируется не только состав частот, но и изменение спектральных характеристик во времени. Это позволяет получать реальную картину перестройки ритма во времени, то есть выявлять объективные характеристики протекающих в организме процессов, которые могут быть использованы для более точной диагностики | ||
== Аналитическое решение задачи построения вейвлет-преобразования для сигнала с частотой, линейно изменяющейся во времени== | == Аналитическое решение задачи построения вейвлет-преобразования для сигнала с частотой, линейно изменяющейся во времени== | ||
| + | |||
| + | Рассмотрим элементарный нестационарный сигнал с частотой <math>f=f_0/T(t-t_0)</math>, линейно меняющейся во времени. | ||
| + | :<math>z(t)=\frac{b}{2τ√π} e^{-\frac{(t-t_0 )^2}{4τ^2}} cos(\frac{ωf_0}{T} (t-t_0 )^2+ωf_0 (t-t_0 )+φ), ω=2π.</math> | ||
==Основные диагностические параметры и спектральные интегралы, получаемые с помощью вейвлет-преобразования== | ==Основные диагностические параметры и спектральные интегралы, получаемые с помощью вейвлет-преобразования== | ||
| Строка 32: | Строка 53: | ||
==Задача классификации пациентов по нескольким диагностическим параметрам (признакам). Метод опорных векторов== | ==Задача классификации пациентов по нескольким диагностическим параметрам (признакам). Метод опорных векторов== | ||
| − | == | + | ==Результаты== |
| + | *Получено аналитичеcкое решение задачи вейвлет-преобразования сигнала с частотой, линейно изменяющейся во времени | ||
| + | *Анализ полученных в результате вейвлет-преобразования характеристик сердечного ритма показал, что экспериментальные данные не подчиняются нормальному закону распределения. | ||
| + | *Для определения целесообразности использования различных признаков при разделении выборки использован метод Манн-Уитни. | ||
| + | *Классификация по двум параметрам позволила выделить группу пациентов (9 человек), состояние которых можно характеризовать как вызывающее опасение. | ||
| + | *Отметим, что все эти пациентки находились в зоне риска и по объективным медицинским показателям. | ||
| + | *Результаты полученные в данной работе подтвердили результаты полученные другими методами. | ||
==Список летературы== | ==Список летературы== | ||
| Строка 65: | Строка 92: | ||
# Дж. Хедли. Нелинейное и динамическое программирование. — М.: Мир, 1967. — 506 с. | # Дж. Хедли. Нелинейное и динамическое программирование. — М.: Мир, 1967. — 506 с. | ||
# Bartlett P., Shawe-Taylor J. Generalization performance of support vector machines and other pattern classifiers // Advances in Kernel Methods. MIT Press, Cambridge, USA, 1998. | # Bartlett P., Shawe-Taylor J. Generalization performance of support vector machines and other pattern classifiers // Advances in Kernel Methods. MIT Press, Cambridge, USA, 1998. | ||
| − | |||
Текущая версия на 11:05, 3 июля 2019
Выпускная квалификационная работа
Выполнил: студент группы 43604/1 А. В. Смирнов
Руководители: кандидат физ.-мат. наук И. Б. Суслова
Содержание
- 1 Актуальность темы
- 2 Цель работы
- 3 Нестационарность биомедицинских сигналов
- 4 Вейвлет-преобразование
- 5 Сравнение Фурье и вейвлет-преборазования
- 6 Аналитическое решение задачи построения вейвлет-преобразования для сигнала с частотой, линейно изменяющейся во времени
- 7 Основные диагностические параметры и спектральные интегралы, получаемые с помощью вейвлет-преобразования
- 8 Задача классификации пациентов по нескольким диагностическим параметрам (признакам). Метод опорных векторов
- 9 Результаты
- 10 Список летературы
Актуальность темы[править]
Медицинская диагностика во много опирается на опыт врача, проводящего осмотр и многочисленные данные в лабораторных исследованиях ( анализ крови, давление и тд.). Развитие медицины в настоящее время предполагает диагностику по записям некоторых количественных характеристик пациента, полученных онлайн, с применением методов классификации состояния пациента (здоров/болен). Анализ состояния пациента по записям ритмограммы сердца с помощью вейвлет-преобразования и методов классификации составляет содержание данной работы.
Цель работы[править]
Построение метода количественной биомедицинской диагностики с использованием интегрального вейвлет-преборазования.
Нестационарность биомедицинских сигналов[править]
Биомедицинские сигналы представляют собой проявления физиологических процессов живого организма, которые могут быть зарегистрированы с помощью различных измерительных приборов и представлены в виде удобном для дальнейшей обработки. Примерами таких сигналов служат: сердечный ритм, дыхательные процессы, температура тела, активность мозга, кровяное давление, режим сна, питания и многие другие. Обработка биосигналов проводится с целью выделения информативных с точки зрения медицинской диагностики признаков заболевания или с целью определения количественных показателей жизнедеятельности организма.
Под нестационарностью сигналов будем понимать изменение во времени спектральных характеристик этих сигналов.Спектральные характеристики биологических сигналов значительно изменяются во времени. Нестационарность ритмов ограничивает возможности применения основных математических методов для обработки записей биомедицинских сигналов. Учет нестационарного характера биоритмов дает дополнительные возможности для изучения этих сигналов и проведения более точной диагностики, что подтверждает необходимость развития соответствующих математических методов.
Вейвлет-преобразование[править]
Интегральное вейвлет преобразование сигнала: задается формулой:
где:
- - Материнский вейвлет, а "" обозначает комплексное сопряжение.
Вейвлет-преобразование отображает исходный сигнал на плоскость непрерывно изменяющихся аргументов – частоты и времени .
Сравнение Фурье и вейвлет-преборазования[править]
Для того, чтобы увидеть все преимущества вейвлет-преобразования в сравнении с преобразованием Фурье, рассмотрим тестовый сигнал:
Для мощности Фурье и вейвлет спектров имеем следующие графики:
Только вейвлет-преобразование выявило момент возникновения каждой частоты и процесс перехода колебаний с одной частотой в колебания другой частоты.
Преимущество вейвлет-преобразования состоит в том, что фиксируется не только состав частот, но и изменение спектральных характеристик во времени. Это позволяет получать реальную картину перестройки ритма во времени, то есть выявлять объективные характеристики протекающих в организме процессов, которые могут быть использованы для более точной диагностики
Аналитическое решение задачи построения вейвлет-преобразования для сигнала с частотой, линейно изменяющейся во времени[править]
Рассмотрим элементарный нестационарный сигнал с частотой , линейно меняющейся во времени.
Основные диагностические параметры и спектральные интегралы, получаемые с помощью вейвлет-преобразования[править]
Задача классификации пациентов по нескольким диагностическим параметрам (признакам). Метод опорных векторов[править]
Результаты[править]
- Получено аналитичеcкое решение задачи вейвлет-преобразования сигнала с частотой, линейно изменяющейся во времени
- Анализ полученных в результате вейвлет-преобразования характеристик сердечного ритма показал, что экспериментальные данные не подчиняются нормальному закону распределения.
- Для определения целесообразности использования различных признаков при разделении выборки использован метод Манн-Уитни.
- Классификация по двум параметрам позволила выделить группу пациентов (9 человек), состояние которых можно характеризовать как вызывающее опасение.
- Отметим, что все эти пациентки находились в зоне риска и по объективным медицинским показателям.
- Результаты полученные в данной работе подтвердили результаты полученные другими методами.
Список летературы[править]
- Божокин С.В., Суслова И.Б., Введение в теорию сигналов. Санкт-Петербург, Изд-во Политехнического университета, 2012. 120 с.
- Г. Бейтмен, А. Эрдейи., Таблицы интегральный преобразований. Т.1. Изд-во Наука. М.1969г.
- Божокин С.В., Суслова И.Б., Основы теории обработки биомедицинских сигналов. Изд-во Политехнического университета, 2016. 151 с.
- Залманзон Л.А., Преобразование Фурье, Уолша, Хаара и их применения в управлении, связи и других областях, Изд-во Наука. М, 1989, 496 с.
- Чуи К. Введение в вейвлеты, Изд-во Мир. М, 2001. 412 с.
- S. Mallat, Wavelet Tour of Signal Processing, 3rd ed. (Academic, New York, 2008).
- Добеши И. Десять лекций по вейвлетам. Изд-во. РЧД. М, 2004.464 с.
- Короновский А.А., Храмов А.Е. Непрерывный вейвлет-анализ и его приложения. Изд-во Физматлит. М, 2003.176с.
- Божокин С.В., Вейвлет-анализ динамики усвоения и забывания ритмов фотостимуляции для нестационарной электроэнцефалограммы, ЖТФ, 2010, Т.80, вып.9, сс 16-24.
- Божокин С.В., Лыков С.Н., Дополнительные главы теоретической физики. Вейвлеты. Учебное пособие, СПб, 2007, 251 с.
- Божокин С.В., Непрерывное вейвлет-преобразование и точно решаемая модель нестационарных сигналов, ЖТФ, 2012, Т.82(7),сс.8-13.
- S. V. Bozhokin, I. M. Suslova. Double wavelet transform of frequency-modulated nonstationary signal, Technical Physics, V. 58(12) (2013) pp.1730-1736 http://link.springer.com/article/10.1134/S1063784213120074
- S.V. Bozhokin, I.B. Suslova, Analysis of non-stationary HRV as a frequency modulated signal by double continuous wavelet transformation method, Biomedical Signal Processing and Control, V.10 (2014) pp.34–40. http://www.sciencedirect.com/science/article/pii/S174680941300181X
- S. V. Bozhokin, I. B. Suslova, Wavelet-based technique to detect gestational complications by analyzing non-stationary heart rate variability, Indian Journal of Fundamental and Applied Life Sciences, V. 5(4), (2015) pp.55-68.
- S. V. Bozhokin, I. B. Suslova, Wavelet Analysis of Non-stationary Signals in Medical Cyber-Physical Systems (MCPS), Lecture Notes in Computer Science, V. 8638 (2014) pp. 467-480, http://link.springer.com/chapter/10.1007/978-3-319-10353-2_42
- Игошева Н.Б., Павлова А.Н., Анищенко Т.Г., Методы анализа сердечного ритма, Изд. Гос УНЦ, «Колледж», Саратов 2001, 120 с.
- Новиков Д.А., Новочадов В.В., Статистические методы в медико-биологическом эксперименте (типовые случаи). Волгоград, изд. ВолГМУ, 2005, .84 c.
- Письменный Д.Т., Конспект лекций по теории вероятностей и математической статистике.-М.:Айрис-Пресс, 2004. 256 с.
- Положинцев Б.И., Теория вероятностей и математическая статистика. Введение в математическую статистику. Учебное пособие, СПб, изд. Политехнического университета, 2010, 96 c.
- Mann H. B., Whitney D. R. On a test of whether one of two random variables is stochastically larger than the other, Annals of Mathematical Statistics, №18, 1947, pp. 50—60.
- Wilcoxon F. Individual Comparisons by Ranking Methods, Biometrics Bulletin 1, 1945, pp. 80-83.
- Гублер Е. В., Генкин А. А. Применение непараметрических критериев статистики в медико-биологических исследованиях. Л., 1973.
- Alexander Statnikov, Constantin F. Aliferis, Douglas P. Hardin. A Gentle Introduction to Support Vector Machines in Biomedicine: Theory and methods. — World Scientific, 2011. ISBN 978-981-4324-38-0.
- Vapnik, Vladimir N.; The Nature of Statistical Learning Theory, Springer-Verlag, 1995. ISBN 0-387-98780-0
- Steinwart, Ingo; and Christmann, Andreas; Support Vector Machines, Springer-Verlag, New York, 2008. ISBN 978-0-387-77241-7 (SVM Book)
- Владимир Вьюгин. Математические основы машинного обучения и прогнозирования. — МЦМНО, 2014. — 304 с. — ISBN 978-5-457-71889-0.
- Nello Cristianini, John Shawe-Taylor. An Introduction to Support Vector Machines and Other Kernel-based Learning Methods. — Cambridge University Press, 2000. — ISBN 978-1-139-64363-4.
- Alexey Nefedov. Support Vector Machines: A Simple Tutorial. — 2016.
- Дж. Хедли. Нелинейное и динамическое программирование. — М.: Мир, 1967. — 506 с.
- Bartlett P., Shawe-Taylor J. Generalization performance of support vector machines and other pattern classifiers // Advances in Kernel Methods. MIT Press, Cambridge, USA, 1998.