Моделирование материала с эффектом памяти формы — различия между версиями
Павел (обсуждение | вклад) |
Павел (обсуждение | вклад) (→Список литературы) |
||
| (не показано 17 промежуточных версий этого же участника) | |||
| Строка 36: | Строка 36: | ||
</gallery> | </gallery> | ||
| − | == | + | ==Эффект памяти формы== |
| − | + | Эффект заключается в способности ненагруженного материала под воз-действием внешнего напряжения и изменения температуры накапливать де-формацию до 10–15%, обратимую при нагреве за счет фазовых превращений (мартенситных). Кинетика мартенситных превращений имеет ярко выраженный гистерезис (рис. 4). Если материал охлаждать из аустенитного состояния, то вначале каких-либо фазовых преобразований не происходит. Однако начиная с некоторой характеристической температуры, которую принято обозначать Ms , появляются первые кристаллы мартенсита, следовательно, увеличивается и доля мартенситной фазы в объеме материала. По мере дальнейшего охлаждения их размеры и количество увеличиваются, пока кристаллы не заполнят при температуре Mf весь объем. Такое превращение называется прямым и при наличии внешней нагрузки сопровождается появлением большой деформации (эффект пластичности превращения). При последующем нагреве, после преодоления температуры As мартенсит начинает переходить в аустенит. При этом накопленная деформация медленно исчезает до тех пор, пока температура не станет выше Af и не произойдет восстановление формы. Температуры мартенситных превращений сильно зависят от химического состава сплавов, их термической и механической обработки. | |
| − | <gallery widths=330px heights= | + | <gallery widths=330px heights=180px perrow = 1> |
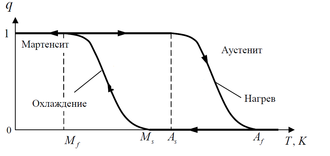
| − | Файл: | + | Файл:Rer.bmp|Рисунок 4. Схема зависимости объемной доли мартенсита q от температуры T |
</gallery> | </gallery> | ||
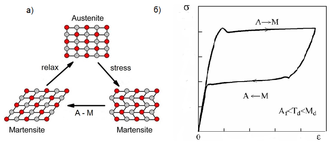
| − | + | Также было отмечено, что механические напряжения инициируют перестройку кристаллической решетки, то есть действуют аналогично температурному фактору. Допустим, что к кристаллу, который находится в аустенитном состоянии при температуре деформирования Тd, начали прикладывать внешнее напряжение. Тогда температура Ms (в соответствии с известным термодинамическим уравнением Клаузиуса-Клапейрона) будет повышаться подобно тому, как растет температура кипения воды под давлением. При каком-то значении напряжения она достигнет значения Тd или превзойдет данный уровень. Это будет означать, что начнется реакция аустенит → мартенсит, которая приведет к образованию мартенсита, наведенного механическими напряжениями. Иными словами, кристалл испытает деформацию по каналу мартенситной неупругости. Если теперь удалить нагрузку, то характеристические температуры (Ms, Mf, Аs, Af) вернутся к первоначальному значению. И тут возможны следующие нетривиальные последствия: когда Тd > Af, возникший мартенсит станет термодинамически абсолютно неустойчивым. Значит, во время снятия нагрузки он с неизбежно превратится в аустенит, а приобретенная деформация полностью вернет-ся – это свойство называется сверхупругостью (рис. 5) [3]. | |
| − | + | <gallery widths=330px heights=180px perrow = 1> | |
| − | + | Файл:B2-R-B19(2).bmp|Рисунок 5. Схема (а) и диаграмма (б), иллюстрирующие эффект сверхупругости в никелиде титана при его деформации в состоянии устойчивого аустенита | |
| − | |||
| − | <gallery widths=330px heights= | ||
| − | Файл: | ||
</gallery> | </gallery> | ||
| − | + | ==Объекты и методы исследования== | |
| − | + | В качестве объектов исследования были выбраны проволочные образцы из сплава Ti‑50.84 ат. %Ni диаметром 0.5 мм и Ti‑50.81 ат. %Ni диаметром 0.7 мм марки ТН-1 фирмы МАТЭК-СПФ. Образцы подвергли различным режимам термообработки: 1 час отжига при 500°C, 2 часа отжига при 500°C и 10 минут при 800°C с последующей закалкой в воде и отжигом при 500°C в течении 2 часов. Данные режимы выбраны, опираясь на исследования, описанные в статье [4]. | |
| − | + | Характеристические температуры, кинетику и последовательность мартенситных превращений в NiTi изучали методом дифференциальной сканирующей калориметрии (ДСК). Образцы массой ~ 5 мг помещали в дифференциальный сканирующий калориметр и определяли температуры и кинетику прямого и обратного мартенситных переходов по зависимостям теплового потока от температуры H(T). При охлаждении и нагревании скорость изменения температуры составляла 10 °С/мин. | |
| − | + | Сверхупругие свойства исследовали методом растяжения образцов (нагрузка-разгрузка) в рабочем диапазоне температур: при комнатной температуре 22°C, температуре человеческого тела ~37°C и при температуре 42°C. Образцы представляли собой отрезки проволоки длиной 7–10 мм, которые помещали в разрывную машину. Диаграммы деформирования получали, нагружая образцы с шагом в 100 МПа с последующей разгрузкой до 0. | |
| − | |||
| − | + | ==Аналитическое решение== | |
| − | + | Для аналитического решения задачи будем использовать модель Мовчана. Микромеханический подход Мовчана заключается в рассмотрении зарождения и развития кристаллов мартенсита, которые дают определенный вклад в скорость изменения фазовой деформации в сплаве с эффектом памяти формы. Предполагается, что скорость роста кристаллов мартенсита пропорциональна накопленной фазовой деформации и уровню напряжений.Общая схема подхода изложена в [5]. Система определяющих соотношений формулируется следующим образом: | |
| − | |||
| − | |||
| − | |||
| − | = | + | <big><math> ε = ε^e + ε^p </math></big>, |
| − | + | где <big><math> ε^e, ε^p </math></big>– тензоры упругой и фазовой деформации. Для упругой деформации справедливы следующие уравнения: | |
| − | + | <big><math> ε'^e = (σ')/2G </math></big>, | |
| − | < | + | <big><math> ε^e= σ/K </math></big>, |
| − | |||
| − | </ | ||
| − | + | где G, K – модули сдвига и объемного сжатия, соответственно. Штрих обозначает девиатор соответствующего тензора. Для фазовой деформации используются уравнения: | |
| − | + | <big><math> dε^p =( c_0 σ' + a_0 ε^p)dq</math></big> при dq > 0, | |
| − | < | + | <big><math> dε^e = ((a_0 ε^0)/((exp(a_0 )-1)) + a_0 ε^p )dq </math></big> при dq < 0, |
| − | |||
| − | |||
| − | </ | ||
| − | + | <big><math>q_1 = cos[π/2 ((T-k√(σ σ )- M_f)/(M_s- M_f )) ] </math></big> при dq > 0, | |
| − | + | <big><math>q_2 = cos[π/2 ((T-k√(σ σ )- A_s)/(A_f- A_s )) ] </math></big> при dq < 0, | |
| − | < | + | <big><math>1/(E(q)) = q/E_1 + (1-q)/E_2 </math></big>. |
| − | |||
| − | |||
| − | </ | ||
| − | + | Здесь Е1, Е2 – значения модуля Юнга для мартенситного и аустенитного со-стояния; a0, k, c0 – коэффициенты материала, которые можно найти из опыта на прямое превращение. Уравнения при dq > 0 соответствуют прямому превращению, а при dq < 0 – обратному. MS, Мf, АS, Аf – температуры начала и завершения прямого и обратного мартенситного превращения. | |
| − | + | ==Решение в ANSYS== | |
| − | <gallery widths= | + | Решать данную задачу будем в ANSYS Mechanical, тип анализа Static Structural (стационарный структурный анализ). Моделируем проволоку, как цилиндр длиной 100 мм и диаметром основания 0.5 мм (в данном случае нам важен именно состав сплава, а не диаметр образца) в 3D постановке, используя элементы Solid, а именно SOLID186.Материал создаем со свойством сверхупругости с константами, взятыми из экспериментальных данных. |
| − | Файл: | + | Начальные и граничные условия задачи будем ставить исходя из реальных условий проведения эксперимента. В начальный момент расчета проволока находится в ненапряженном состоянии, температура среды равна Td. Граничные условия схематично показаны на рисунке 6. Закрепляем нижнюю грань цилиндра, на верхнюю задаем перемещение вдоль оси z, равное максимуму обратимой деформации. |
| + | <gallery widths=200px heights=300px perrow = 1> | ||
| + | Файл:Brab.bmp|Рисунок 6. Постановка задачи | ||
</gallery> | </gallery> | ||
| − | + | ==Результаты== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
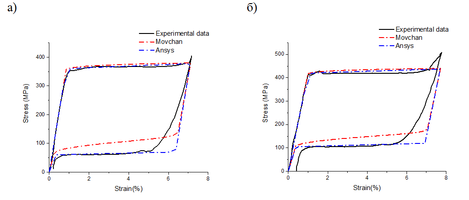
| − | + | Сравним результаты аналитического решения, посчитанные в Wolfram Mathematica, с решением в ANSYS и экспериментальными данными. Рассчитывались только те варианты, в которых у проволочных образцов проявилось свойство сверхупругости. | |
| − | + | <gallery widths=500px heights=200px perrow = 1> | |
| − | + | Файл:Psevd.bmp|Рисунок 7. Диаграммы деформирования образцов из сплава Ti‑50.84 ат. %Ni диаметром 0.5 мм при температуре 37⁰С (а) и 42⁰С (б) после 1 часа отжига при 500⁰С | |
| − | <gallery widths= | ||
| − | Файл: | ||
| − | |||
</gallery> | </gallery> | ||
| − | + | Полученные результаты качественно сходятся с экспериментальными данными. Константы, использованные при расчете одноосного растяжения, можно использовать для прогнозирования поведения материала при более сложных деформациях. Но стоит отметить, что данные методы решения не учитывают остаточную деформацию. | |
| − | == | + | ==Выводы== |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | В ходе работы экспериментальным путем были изучены функционально-механические свойства проволочных образцов из медицинского никель-обогащенного никелида титана марки ТН-1, как материала для устройства, устраняющего пролапс митрального клапана. Образцы были двух видов: Ti‑50.84 ат. %Ni диаметром 0.5 мм и Ti‑50.81 ат. %Ni диаметром 0.7 мм. Также образцы отличались по режимам термообработки: 1 час отжига при 500°C, 2 часа отжига при 500°C и 10 мин при 800°C с последующей закалкой + 2 час отжига при 500°C. Эксперименты проводились при комнатной температуре 22°C, температуре человеческого тела ~37°C и при температуре 42°C. У большинства образцов было отмечено проявления свойства сверхупругости. При этом максимальная обратимая деформация с наименьшей остаточной была у образца из сплава Ti‑50.81 ат. %Ni, подвергнутому 1 часу отжига при 500°C. При температуре эксперимента 22°C его обратимая деформация достигла 9.7% с остаточной 0.25% с пределом текучести 460 МПа. | |
| − | + | По данным эксперимента были проведены расчеты одноосного растяжения двумя методами: микромеханическим подходом Мовчана для сплавов с ЭПФ и методом конечных элементов в программной системе ANSYS Mechanical. | |
| − | + | При численном решении данной задачи в ANSYS был выбран тип анализа Static Structural (стационарный структурный анализ). Данный тип анализа позволяет определять перемещения, деформации, напряжения и внутренние усилия в теле под воздействием нагрузок медленно меняющихся во времени, которые не вызывают инерционных и демпфирующих эффектов. Материал был задан как нелинейный со свойством сверхупругости. | |
| − | + | Микромеханический подход Мовчана заключается в рассмотрении зарождения и развития кристаллов мартенсита, которые дают определенный вклад в скорость изменения фазовой деформации в сплаве с памятью формы. Данная модель позволяет получать аналитические зависимости для фазовой деформации. | |
| − | + | Оба метода показали качественную сходимость с экспериментальными данными. Но стоит отметить, что данные методы решения не учитывают остаточную деформацию. Константами материала, полученными при моделировании одноосного напряжения можно пользоваться и для прогнозирования более сложных деформаций. В дальнейшем в рамках данного проекта планируется моделирование самого устройства, устраняющего пролапс митрального клапана. | |
| − | + | Результаты данной работы были представлены на конференции «Сплавы с эффектом памяти формы», посвященной 85-летию В.А. Лихачева и опубликованы в журнале «Materials Today: Proceedings» (цитируется Scopus) [6]. | |
==Список литературы== | ==Список литературы== | ||
| − | 1. | + | 1. E. Hayek, C.N. Gring, B.P. Griffin. Lancet. 365 (2005) 507-518. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 2. E.N. Feins, H. Yamauchi, G.R. Marx, F.P. Freudenthal, H. Liu, P.J. del Nido, N.V. Vasilyev. J Thorac Cardiovasc Surg. 147 (2014) 783-791. | |
| − | |||
| − | |||
| − | + | 3. Лихачев В.А., Кузьмин С.Л., Каменцева З.П. Эффект памяти формы. // Л.: Изд-во ЛГУ, 1987. 218 с. | |
| − | + | 4. V.G. Dorodeiko, V.V. Rubanik, V.V. Rubanik Jr., and S.N. Miljukina. Making intrauterine contraceptives from TiNi alloys. // 7th European Symposium on Martensitic Transfor-mations ESOMAT. 2006: Abstracts. Bochum/Germany. 2006. P. 312. | |
| − | + | 5. А.А. Мовчан. Микромеханические определяющие уравнения для сплавов с памятью формы. // Проблемы машиностроения и надежности машин. 1994. № 6. С. 47–53. | |
| − | + | 6. Buldakov P.Y., Resnina N.N., Chumachenko A.V., Stepanov M.D., del Nido P.J., Loboda O.S., Vasilyev N.V. Functional and mechanical properties of the NiTi TN-1alloy as a material for an implantable device for mitral valve prolapce.\\ Materials Today: Proceedings.Volume 4. Issue 3. Part B. 2017. P. 4884–4888. | |
Текущая версия на 21:32, 20 июня 2017
Выпускная квалификационная работа
Выполнил: студент группы 43604/1 П.Ю. Булдаков
Руководитель: кандидат физ.-мат. наук, доцент каф. "Теоретическая механика" О.С. Лобода
Содержание
Введение[править]
В последнее время в науке, технике и медицине все большее применение находят многофункциональные материалы с заданными свойствами – материалы, которые под действием внешних факторов и условий эксплуатации (температуры, механической нагрузки и т.д.) могут управляемо изменять свои свойства. Безусловно, к таким материалам относятся сплавы с уникальными и совсем недавно неизвестными физико-механическими свойствами – эффектом памяти формы (ЭПФ), явление возврата к первоначальной форме при нагреве после пластической деформации. Это явление наблюдается у некоторых материалов после предварительной деформации в строго определенном для каждого сплава интервале температур. Связан эффект с особым видом пластической деформации – мартенситными превращениями.
Цель и задачи работы[править]
Моделирование сплава с ЭПФ рассмотрено в контексте проекта, в котором изучались функционально-механические свойства сплава, как материла для устройства, устраняющего пролапс митрального клапана. В качестве материала был выбран сплав никелида титана NiTi марки ТН-1. Цель данной работы заключалась в моделировании поведения проволоки из данного сплава при одноосном растяжении. В связи с поставленной целью в работе решаются следующие задачи:
• Экспериментально исследовать функционально – механические свойства никелида титана Ti - 50.84 ат. %Ni диаметром 0.5 мм и Ti - 50.81 ат. %Ni диаметром 0.7 мм марки ТН-1 фирмы МАТЭК-СПФ при разных температурах окружающей среды после различных режимов термообработки;
• По данным эксперимента провести расчеты одноосного растяжения двумя методами: микромеханическим подходом Мовчана для сплавов с ЭПФ и методом конечных элементов в программной системе ANSYS Mechanical;
• Сравнить результаты расчетов с экспериментальными данными;
Пролапс митрального клапана и его коррекция[править]
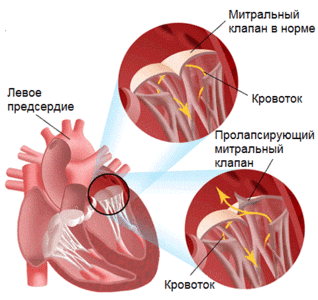
Пролапс митрального клапана (ПМК) (рис. 1) – это провисание створок митрального клапана в полость левого предсердия во время систолы, что при-водит к обратному току крови через клапан и может вызвать такие осложнения, как эндокардит, разрыв хорд и тромбоэмболия. Распространенность ПМК среди населения по одним данным оценена в 2–3% [1], по другим в 5–10% (у взрослой популяции). В большинстве случаев хирургическое вмешательство не требуется, но при высокой степени провисания створки необходима дорогостоящая операция с большим риском для жизни, так как для ее проведения требуется остановка сердца.
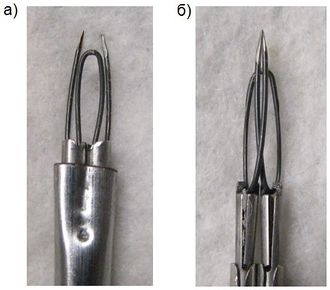
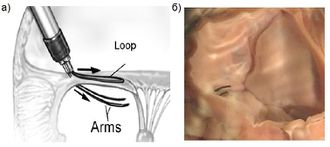
LPC (Leaflet Plication Clip) [2] был разработан в Бостонской детской больнице и представляет из себя специально изогнутую проволоку из сплава никелид-титана (NiTi). Установка LPC (рис.3) на пролапсирующий митральный клапан является альтернативой хирургическому методу лечения и может быть выполнена без остановки сердца. LPC изначально задают форму как показано на рисунке 2 (б). Во время операции его «взводят» (рис. 2, 3 а) при помощи специального инструмента и крепят на пролапсирующую створку митрального клапана, за счет того, что он выполнен из материала с ЭПФ, LPC «схлопывается» в свою исходную форму, тем самым сжимая провисающую часть створки и прекращая митральную регургитацию (ток крови в обратную сторону) (рис. 3 б). В данном случае используется свойство cверхупругости, которое присуще материалам с ЭПФ.
Эффект памяти формы[править]
Эффект заключается в способности ненагруженного материала под воз-действием внешнего напряжения и изменения температуры накапливать де-формацию до 10–15%, обратимую при нагреве за счет фазовых превращений (мартенситных). Кинетика мартенситных превращений имеет ярко выраженный гистерезис (рис. 4). Если материал охлаждать из аустенитного состояния, то вначале каких-либо фазовых преобразований не происходит. Однако начиная с некоторой характеристической температуры, которую принято обозначать Ms , появляются первые кристаллы мартенсита, следовательно, увеличивается и доля мартенситной фазы в объеме материала. По мере дальнейшего охлаждения их размеры и количество увеличиваются, пока кристаллы не заполнят при температуре Mf весь объем. Такое превращение называется прямым и при наличии внешней нагрузки сопровождается появлением большой деформации (эффект пластичности превращения). При последующем нагреве, после преодоления температуры As мартенсит начинает переходить в аустенит. При этом накопленная деформация медленно исчезает до тех пор, пока температура не станет выше Af и не произойдет восстановление формы. Температуры мартенситных превращений сильно зависят от химического состава сплавов, их термической и механической обработки.
Также было отмечено, что механические напряжения инициируют перестройку кристаллической решетки, то есть действуют аналогично температурному фактору. Допустим, что к кристаллу, который находится в аустенитном состоянии при температуре деформирования Тd, начали прикладывать внешнее напряжение. Тогда температура Ms (в соответствии с известным термодинамическим уравнением Клаузиуса-Клапейрона) будет повышаться подобно тому, как растет температура кипения воды под давлением. При каком-то значении напряжения она достигнет значения Тd или превзойдет данный уровень. Это будет означать, что начнется реакция аустенит → мартенсит, которая приведет к образованию мартенсита, наведенного механическими напряжениями. Иными словами, кристалл испытает деформацию по каналу мартенситной неупругости. Если теперь удалить нагрузку, то характеристические температуры (Ms, Mf, Аs, Af) вернутся к первоначальному значению. И тут возможны следующие нетривиальные последствия: когда Тd > Af, возникший мартенсит станет термодинамически абсолютно неустойчивым. Значит, во время снятия нагрузки он с неизбежно превратится в аустенит, а приобретенная деформация полностью вернет-ся – это свойство называется сверхупругостью (рис. 5) [3].
Объекты и методы исследования[править]
В качестве объектов исследования были выбраны проволочные образцы из сплава Ti‑50.84 ат. %Ni диаметром 0.5 мм и Ti‑50.81 ат. %Ni диаметром 0.7 мм марки ТН-1 фирмы МАТЭК-СПФ. Образцы подвергли различным режимам термообработки: 1 час отжига при 500°C, 2 часа отжига при 500°C и 10 минут при 800°C с последующей закалкой в воде и отжигом при 500°C в течении 2 часов. Данные режимы выбраны, опираясь на исследования, описанные в статье [4]. Характеристические температуры, кинетику и последовательность мартенситных превращений в NiTi изучали методом дифференциальной сканирующей калориметрии (ДСК). Образцы массой ~ 5 мг помещали в дифференциальный сканирующий калориметр и определяли температуры и кинетику прямого и обратного мартенситных переходов по зависимостям теплового потока от температуры H(T). При охлаждении и нагревании скорость изменения температуры составляла 10 °С/мин. Сверхупругие свойства исследовали методом растяжения образцов (нагрузка-разгрузка) в рабочем диапазоне температур: при комнатной температуре 22°C, температуре человеческого тела ~37°C и при температуре 42°C. Образцы представляли собой отрезки проволоки длиной 7–10 мм, которые помещали в разрывную машину. Диаграммы деформирования получали, нагружая образцы с шагом в 100 МПа с последующей разгрузкой до 0.
Аналитическое решение[править]
Для аналитического решения задачи будем использовать модель Мовчана. Микромеханический подход Мовчана заключается в рассмотрении зарождения и развития кристаллов мартенсита, которые дают определенный вклад в скорость изменения фазовой деформации в сплаве с эффектом памяти формы. Предполагается, что скорость роста кристаллов мартенсита пропорциональна накопленной фазовой деформации и уровню напряжений.Общая схема подхода изложена в [5]. Система определяющих соотношений формулируется следующим образом:
,
где – тензоры упругой и фазовой деформации. Для упругой деформации справедливы следующие уравнения:
,
,
где G, K – модули сдвига и объемного сжатия, соответственно. Штрих обозначает девиатор соответствующего тензора. Для фазовой деформации используются уравнения:
при dq > 0,
при dq < 0,
при dq > 0,
при dq < 0,
.
Здесь Е1, Е2 – значения модуля Юнга для мартенситного и аустенитного со-стояния; a0, k, c0 – коэффициенты материала, которые можно найти из опыта на прямое превращение. Уравнения при dq > 0 соответствуют прямому превращению, а при dq < 0 – обратному. MS, Мf, АS, Аf – температуры начала и завершения прямого и обратного мартенситного превращения.
Решение в ANSYS[править]
Решать данную задачу будем в ANSYS Mechanical, тип анализа Static Structural (стационарный структурный анализ). Моделируем проволоку, как цилиндр длиной 100 мм и диаметром основания 0.5 мм (в данном случае нам важен именно состав сплава, а не диаметр образца) в 3D постановке, используя элементы Solid, а именно SOLID186.Материал создаем со свойством сверхупругости с константами, взятыми из экспериментальных данных. Начальные и граничные условия задачи будем ставить исходя из реальных условий проведения эксперимента. В начальный момент расчета проволока находится в ненапряженном состоянии, температура среды равна Td. Граничные условия схематично показаны на рисунке 6. Закрепляем нижнюю грань цилиндра, на верхнюю задаем перемещение вдоль оси z, равное максимуму обратимой деформации.
Результаты[править]
Сравним результаты аналитического решения, посчитанные в Wolfram Mathematica, с решением в ANSYS и экспериментальными данными. Рассчитывались только те варианты, в которых у проволочных образцов проявилось свойство сверхупругости.
Полученные результаты качественно сходятся с экспериментальными данными. Константы, использованные при расчете одноосного растяжения, можно использовать для прогнозирования поведения материала при более сложных деформациях. Но стоит отметить, что данные методы решения не учитывают остаточную деформацию.
Выводы[править]
В ходе работы экспериментальным путем были изучены функционально-механические свойства проволочных образцов из медицинского никель-обогащенного никелида титана марки ТН-1, как материала для устройства, устраняющего пролапс митрального клапана. Образцы были двух видов: Ti‑50.84 ат. %Ni диаметром 0.5 мм и Ti‑50.81 ат. %Ni диаметром 0.7 мм. Также образцы отличались по режимам термообработки: 1 час отжига при 500°C, 2 часа отжига при 500°C и 10 мин при 800°C с последующей закалкой + 2 час отжига при 500°C. Эксперименты проводились при комнатной температуре 22°C, температуре человеческого тела ~37°C и при температуре 42°C. У большинства образцов было отмечено проявления свойства сверхупругости. При этом максимальная обратимая деформация с наименьшей остаточной была у образца из сплава Ti‑50.81 ат. %Ni, подвергнутому 1 часу отжига при 500°C. При температуре эксперимента 22°C его обратимая деформация достигла 9.7% с остаточной 0.25% с пределом текучести 460 МПа.
По данным эксперимента были проведены расчеты одноосного растяжения двумя методами: микромеханическим подходом Мовчана для сплавов с ЭПФ и методом конечных элементов в программной системе ANSYS Mechanical.
При численном решении данной задачи в ANSYS был выбран тип анализа Static Structural (стационарный структурный анализ). Данный тип анализа позволяет определять перемещения, деформации, напряжения и внутренние усилия в теле под воздействием нагрузок медленно меняющихся во времени, которые не вызывают инерционных и демпфирующих эффектов. Материал был задан как нелинейный со свойством сверхупругости.
Микромеханический подход Мовчана заключается в рассмотрении зарождения и развития кристаллов мартенсита, которые дают определенный вклад в скорость изменения фазовой деформации в сплаве с памятью формы. Данная модель позволяет получать аналитические зависимости для фазовой деформации.
Оба метода показали качественную сходимость с экспериментальными данными. Но стоит отметить, что данные методы решения не учитывают остаточную деформацию. Константами материала, полученными при моделировании одноосного напряжения можно пользоваться и для прогнозирования более сложных деформаций. В дальнейшем в рамках данного проекта планируется моделирование самого устройства, устраняющего пролапс митрального клапана.
Результаты данной работы были представлены на конференции «Сплавы с эффектом памяти формы», посвященной 85-летию В.А. Лихачева и опубликованы в журнале «Materials Today: Proceedings» (цитируется Scopus) [6].
Список литературы[править]
1. E. Hayek, C.N. Gring, B.P. Griffin. Lancet. 365 (2005) 507-518.
2. E.N. Feins, H. Yamauchi, G.R. Marx, F.P. Freudenthal, H. Liu, P.J. del Nido, N.V. Vasilyev. J Thorac Cardiovasc Surg. 147 (2014) 783-791.
3. Лихачев В.А., Кузьмин С.Л., Каменцева З.П. Эффект памяти формы. // Л.: Изд-во ЛГУ, 1987. 218 с.
4. V.G. Dorodeiko, V.V. Rubanik, V.V. Rubanik Jr., and S.N. Miljukina. Making intrauterine contraceptives from TiNi alloys. // 7th European Symposium on Martensitic Transfor-mations ESOMAT. 2006: Abstracts. Bochum/Germany. 2006. P. 312.
5. А.А. Мовчан. Микромеханические определяющие уравнения для сплавов с памятью формы. // Проблемы машиностроения и надежности машин. 1994. № 6. С. 47–53.
6. Buldakov P.Y., Resnina N.N., Chumachenko A.V., Stepanov M.D., del Nido P.J., Loboda O.S., Vasilyev N.V. Functional and mechanical properties of the NiTi TN-1alloy as a material for an implantable device for mitral valve prolapce.\\ Materials Today: Proceedings.Volume 4. Issue 3. Part B. 2017. P. 4884–4888.