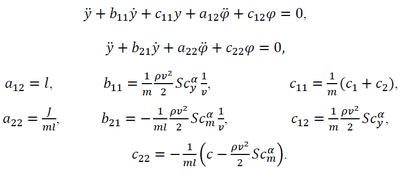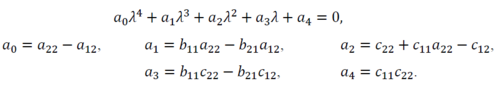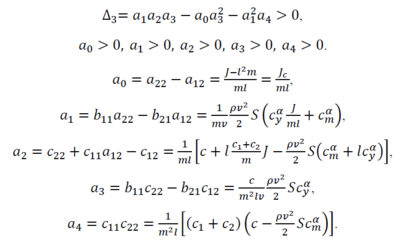Исследование критической скорости флаттера крыла Clark YH 8% — различия между версиями
(Новая страница: «Флаттер (от англ. flutter — дрожание, вибрация) — сочетание самовозбуждающихся незатухающи…») |
(→Визуализация) |
||
| (не показано 11 промежуточных версий 3 участников) | |||
| Строка 4: | Строка 4: | ||
При движении самолета на определенной скорости возникает флаттер, который характеризуется нарастающими автоколебаниями различных упругих частей самолета: крыльев, элеронов, закрылок, рулей поворота, рулей высоты др. Флаттер приводит к быстрому разрушению всего самолета в целом. Одним из решений этой проблемы, является расчет критической скорости (скорость флаттера), которую самолет не должен превысить. | При движении самолета на определенной скорости возникает флаттер, который характеризуется нарастающими автоколебаниями различных упругих частей самолета: крыльев, элеронов, закрылок, рулей поворота, рулей высоты др. Флаттер приводит к быстрому разрушению всего самолета в целом. Одним из решений этой проблемы, является расчет критической скорости (скорость флаттера), которую самолет не должен превысить. | ||
В рамках этой работы были поставлены задачи: | В рамках этой работы были поставлены задачи: | ||
| − | + | ||
| − | + | 1. Изучить задачу о крутильно-изгибном флаттере крыла при дозвуковых скоростях, пренебрегая некоторыми аэродинамическими параметрами | |
| + | |||
| + | 2. Создать интерактивную модель этого процесса на JavaScript с помощью библиотеки three.js | ||
| + | |||
В данной работе выполнен расчет критической скорости крыла Clark YH 8%, при этом есть возможность изменять характеристики крыла и угол атаки для исследования критической скорости и наблюдением за колебаниями системы. | В данной работе выполнен расчет критической скорости крыла Clark YH 8%, при этом есть возможность изменять характеристики крыла и угол атаки для исследования критической скорости и наблюдением за колебаниями системы. | ||
| + | |||
| + | == Теоретическая часть задачи == | ||
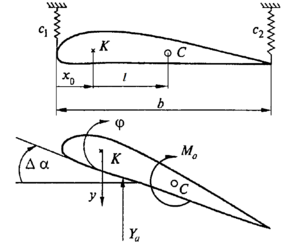
| + | [[File:flutter001.PNG|300px|thumb|right|К — центр жесткости, С — центр тяжести крыла, c1 и c2 — коэффициенты жесткости крыла. За обобщенные координаты примем: y — линейную координату отклонения центра жесткости крыла при изгибе, φ — угловую]] | ||
| + | |||
| + | При флаттере крыло совершает сложные гармонические колебания. Ограничимся в первом приближении рассмотрением плоских колебания крыла в потоке воздуха. Так как конструкция реального крыла, состоящая из разного рода элементов (закрылки, элероны и т.д.), достаточно сложная, то рассмотрим его в виде жесткой модели крыла с упругими связями. | ||
| + | |||
| + | Предположим, что система имеет две степени свободы, причем пружины (упругие связи) обеспечивают только вертикальные движения точек крепления крыла. | ||
| + | |||
| + | Составим систему из двух дифференциальных уравнений колебаний крыла, применив для этого уравнения Лагранжа II рода, где обобщенными силами будут потенциальные силы упругой связи и аэродинамические силы, тогда получим: | ||
| + | |||
| + | [[File:flutter002.PNG|400px]] | ||
| + | |||
| + | Решение полученной системы уравнений будем разыскивать в виде y=Aexp(λt), φ=Bexp(λt). Получим характеристическое уравнение, приравниваем его к нулю, так как для ненулевого решения определитель системы уравнений должен быть равен нулю. | ||
| + | |||
| + | [[File:flutter04.png|500px]] | ||
| + | |||
| + | Заключение об устойчивости или неустойчивости системы можно сделать, применив критерий устойчивости Гурвица. Для устойчивости уравнения четвертого порядка необходимо, что бы определитель третьего порядка был больше нуля и все коэффициенты характеристического уравнения также были больше нуля. | ||
| + | |||
| + | [[File:flutter003.png|400px]] | ||
| + | |||
| + | Из полученных выражений ясно, что при постоянном значении величины l, знаки коэффициентов a0,a1,a3 не зависят от скорости полета v, знаки коэффициентов a2,a4, наоборот, зависят от скорости v. | ||
| + | |||
| + | Расчеты показывают, что условие положительности коэффициентов выполняются автоматически, а критическая скорость определяется из численного решения неравенства. | ||
| + | |||
== Визуализация == | == Визуализация == | ||
| + | Во вкладке "Initial conditions" (начальные условия) можно изменять следующие параметры: | ||
| + | * chord - величина хорды профиля крыла | ||
| + | * length - длина крыла | ||
| + | * numZ - количество разбиений | ||
| + | * mass - масса крыла | ||
| + | * alpha - угол атаки | ||
| + | * c1 и с2 - коэффициенты жесткости | ||
| + | В "Results" выводится результат расчетов критической скорости системы при данных параметрах. | ||
| + | |||
| + | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Abramov_IA/Flutter/flutter.html |width=1300 |height=750 |border=0 }} | ||
| + | == Участники проекта == | ||
| + | * [http://tm.spbstu.ru/%D0%90%D0%B1%D1%80%D0%B0%D0%BC%D0%BE%D0%B2_%D0%98%D0%B3%D0%BE%D1%80%D1%8C Абрамов Игорь] | ||
| + | * [http://tm.spbstu.ru/%D0%91%D0%B0%D0%BB%D1%8C%D1%86%D0%B5%D1%80_%D0%90%D0%BD%D0%B0%D1%81%D1%82%D0%B0%D1%81%D0%B8%D1%8F Бальцер Анастасия] | ||
== Материалы проекта == | == Материалы проекта == | ||
| + | |||
| + | [[:File:Flutter Abramov Baltser.pdf|Полное описание работы]] | ||
| + | |||
| + | [[:File:Flutter.rar|Архив с кодом проекта]] | ||
| + | |||
| + | [https://www.youtube.com/watch?v=qpJBvQXQC2M Видео, на котором показан флаттер в разных проявлениях] | ||
| + | |||
| + | [http://kipla.kai.ru/liter/Spravochnic_avia_profiley.pdf Справочник авиационных профилей] | ||
| + | |||
| + | [http://mid-journal.ru/upload/iblock/934/934ecd2a6e322cf779f9d66dc11c46e6.pdf А. А. Кузнецов, А. А. Матросов «Условия возникновения флаттера крыла самолета АН-124-100» ] | ||
Текущая версия на 13:52, 7 июня 2017
Флаттер (от англ. flutter — дрожание, вибрация) — сочетание самовозбуждающихся незатухающих изгибающих и крутящих автоколебаний элементов конструкции летательного аппарата — главным образом крыла самолёта либо несущего винта вертолёта.
Содержание
Введение[править]
При движении самолета на определенной скорости возникает флаттер, который характеризуется нарастающими автоколебаниями различных упругих частей самолета: крыльев, элеронов, закрылок, рулей поворота, рулей высоты др. Флаттер приводит к быстрому разрушению всего самолета в целом. Одним из решений этой проблемы, является расчет критической скорости (скорость флаттера), которую самолет не должен превысить. В рамках этой работы были поставлены задачи:
1. Изучить задачу о крутильно-изгибном флаттере крыла при дозвуковых скоростях, пренебрегая некоторыми аэродинамическими параметрами
2. Создать интерактивную модель этого процесса на JavaScript с помощью библиотеки three.js
В данной работе выполнен расчет критической скорости крыла Clark YH 8%, при этом есть возможность изменять характеристики крыла и угол атаки для исследования критической скорости и наблюдением за колебаниями системы.
Теоретическая часть задачи[править]
При флаттере крыло совершает сложные гармонические колебания. Ограничимся в первом приближении рассмотрением плоских колебания крыла в потоке воздуха. Так как конструкция реального крыла, состоящая из разного рода элементов (закрылки, элероны и т.д.), достаточно сложная, то рассмотрим его в виде жесткой модели крыла с упругими связями.
Предположим, что система имеет две степени свободы, причем пружины (упругие связи) обеспечивают только вертикальные движения точек крепления крыла.
Составим систему из двух дифференциальных уравнений колебаний крыла, применив для этого уравнения Лагранжа II рода, где обобщенными силами будут потенциальные силы упругой связи и аэродинамические силы, тогда получим:
Решение полученной системы уравнений будем разыскивать в виде y=Aexp(λt), φ=Bexp(λt). Получим характеристическое уравнение, приравниваем его к нулю, так как для ненулевого решения определитель системы уравнений должен быть равен нулю.
Заключение об устойчивости или неустойчивости системы можно сделать, применив критерий устойчивости Гурвица. Для устойчивости уравнения четвертого порядка необходимо, что бы определитель третьего порядка был больше нуля и все коэффициенты характеристического уравнения также были больше нуля.
Из полученных выражений ясно, что при постоянном значении величины l, знаки коэффициентов a0,a1,a3 не зависят от скорости полета v, знаки коэффициентов a2,a4, наоборот, зависят от скорости v.
Расчеты показывают, что условие положительности коэффициентов выполняются автоматически, а критическая скорость определяется из численного решения неравенства.
Визуализация[править]
Во вкладке "Initial conditions" (начальные условия) можно изменять следующие параметры:
- chord - величина хорды профиля крыла
- length - длина крыла
- numZ - количество разбиений
- mass - масса крыла
- alpha - угол атаки
- c1 и с2 - коэффициенты жесткости
В "Results" выводится результат расчетов критической скорости системы при данных параметрах.
Участники проекта[править]
Материалы проекта[править]
Видео, на котором показан флаттер в разных проявлениях
Справочник авиационных профилей
А. А. Кузнецов, А. А. Матросов «Условия возникновения флаттера крыла самолета АН-124-100»