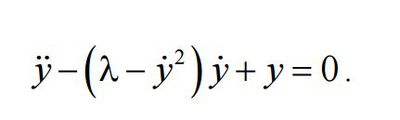Исследование уравнения Рэлея — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
(Новая страница: «рис.1 == Введение == Уравнение Рэлея(рис.1) - дифференциальное уравне…») |
(→Программа) |
||
| (не показано 13 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
[[File:bGN4OiMQvo8.jpg|400px|thumb|right|рис.1]] | [[File:bGN4OiMQvo8.jpg|400px|thumb|right|рис.1]] | ||
| − | == | + | == Описание задачи == |
Уравнение Рэлея(рис.1) - дифференциальное уравнение 2 порядка,которое описывает нелинейную систему с одной степенью свободы, | Уравнение Рэлея(рис.1) - дифференциальное уравнение 2 порядка,которое описывает нелинейную систему с одной степенью свободы, | ||
| − | в которой возможны автоколебания,где λ – параметр колебательной системы.Автоколебания —незатухающие колебания, поддерживаемые внеш. источниками энергии, в нелинейной диссипативной системе | + | в которой возможны автоколебания,где λ – параметр колебательной системы.Автоколебания —незатухающие колебания, поддерживаемые внеш. источниками энергии, в нелинейной диссипативной системе. |
| − | + | ||
| − | + | Задачи : | |
| − | + | ||
1.Проанализировать уравнение с помощью метода Ван дер Поля при малых значениях параметра. | 1.Проанализировать уравнение с помощью метода Ван дер Поля при малых значениях параметра. | ||
| Строка 11: | Строка 11: | ||
3. Понять, как влияет величина параметра на характер колебаний. | 3. Понять, как влияет величина параметра на характер колебаний. | ||
| + | |||
| + | == Презентация == | ||
| + | [http://tm.spbstu.ru/File:Rel.pptx Скачать презентацию] | ||
| + | |||
| + | == Программа == | ||
| + | |||
| + | Построение фазовых портретов в Matlab. | ||
| + | |||
| + | [http://tm.spbstu.ru/File:fazovie_ploskosti.rar Скачать программу] | ||
| + | |||
| + | == Участники проекта == | ||
| + | |||
| + | * [http://tm.spbstu.ru/Лосева_Татьяна Лосева Татьяна] | ||
| + | |||
| + | == См. также == | ||
| + | [[Кафедра "Теоретическая механика"]] | ||
Текущая версия на 00:35, 5 июня 2017
Описание задачи[править]
Уравнение Рэлея(рис.1) - дифференциальное уравнение 2 порядка,которое описывает нелинейную систему с одной степенью свободы, в которой возможны автоколебания,где λ – параметр колебательной системы.Автоколебания —незатухающие колебания, поддерживаемые внеш. источниками энергии, в нелинейной диссипативной системе.
Задачи :
1.Проанализировать уравнение с помощью метода Ван дер Поля при малых значениях параметра.
2.Построить фазовые траектории.
3. Понять, как влияет величина параметра на характер колебаний.
Презентация[править]
Программа[править]
Построение фазовых портретов в Matlab.