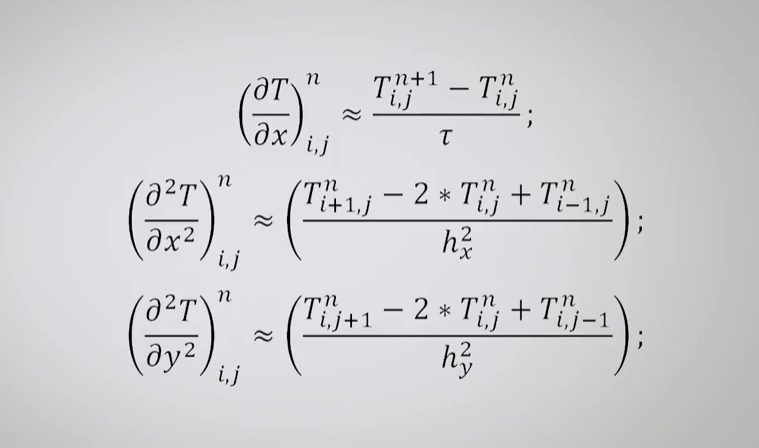Решение двумерного уравнения теплопроводности. Черногорский Вячеслав. 6 курс — различия между версиями
Igolf (обсуждение | вклад) |
Igolf (обсуждение | вклад) |
||
| Строка 34: | Строка 34: | ||
|- | |- | ||
|1 | |1 | ||
| − | | | + | |8.32 |
|- | |- | ||
|4 | |4 | ||
| − | | | + | |3.15 |
|- | |- | ||
|9 | |9 | ||
| − | | | + | |270.68 |
|- | |- | ||
Текущая версия на 03:31, 20 февраля 2017
Содержание
Цель[править]
Численное решение уравнения теплопроводности в единичном квадрате с помощью функций библиотеки MPI.
Постановка задачи[править]
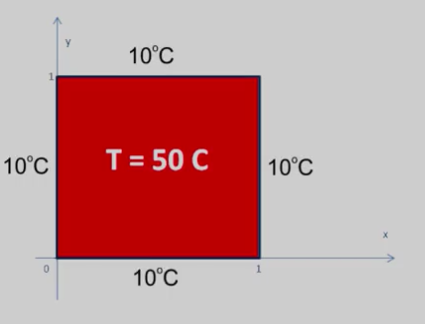
Имеется пластина в форме квадрата с ребром единичной длины. Пусть пластина разогрета до температуры Тнач., и затем помещена в среду, которая имеет отличную температуру Тсреды. В этой задаче нас интересует процесс численного решения уравнения теплопроводности для пластины, которое выглядит следующим образом:
С граничными условиями
И начальным распределением температуры
Конечно-разностная схема[править]
Задача содержит производную по времени первого порядка и производные по пространственным координатам второго порядка. Запишем конечно-разностные аналоги слагаемых, входящих в уравнение
Компьютерная реализация[править]
Компьютерную реализацию программы можно найти в Файл:Teplo.rar. В первую очередь область исследования покрывается конечно-разностной сеткой, и решение мы будем искать в узлах этой сетки. Для граничных узлов сетки, решение уже известно из граничных условий, для внутренних условий решение мы должны найти. Так как процесс у нас протекающий во времени, то решение мы будем искать по слоям сетки, в пределах заданного времени.
Результаты[править]
| Количество процессов | Время рассчета (сек) |
|---|---|
| 1 | 8.32 |
| 4 | 3.15 |
| 9 | 270.68 |
Выводы[править]
- При использовании 4 процессов скорость расчета наиболее оптимальна.
- При увеличении числа процессоров скорость расчета уменьшается.