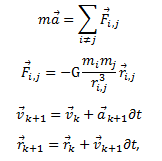Движение небесных тел — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
м |
|||
| (не показано 5 промежуточных версий 1 участника) | |||
| Строка 10: | Строка 10: | ||
* Интегрирование производится методом Эйлера; | * Интегрирование производится методом Эйлера; | ||
| − | + | == Используемые формулы == | |
| + | |||
| + | [[File:Screenshot_1.png]] | ||
| + | |||
| + | где i, j – это индексы небесных тел, а k – номер итерации. | ||
== Результаты == | == Результаты == | ||
| Строка 24: | Строка 28: | ||
* [[Сызранцев Денис]] | * [[Сызранцев Денис]] | ||
| − | * [[ | + | * [[Дегтерев Данил]] |
* [[Порубенко Мария]] | * [[Порубенко Мария]] | ||
* [[Калоева Диана]] | * [[Калоева Диана]] | ||
* [[Лямина Арина]] | * [[Лямина Арина]] | ||
Текущая версия на 15:15, 22 сентября 2018
Содержание
Предыстория[править]
Изучение Солнечной системы стало началом современной небесной механики, рождённой трудами И. Кеплера (1571—1630) и И. Ньютона (1643—1727). Кеплер впервые установил законы планетного движения, а Ньютон вывел из законов Кеплера закон всемирного тяготения и использовал законы движения и тяготения для решения небесно-механических проблем, не охваченных законами Кеплера. После Ньютона прогресс в небесной механике в основном заключался в развитии математической техники для решения уравнений, выражающих законы Ньютона.
Содержание работы[править]
- В качестве объекта исследования берётся замкнутая система, состоящая из тел Солнечной системы (Солнце, Земля и Луна);
- Абстракциями небесных тел являются материальные точки;
- Использование классической механики Ньютона;
- Интегрирование производится методом Эйлера;
Используемые формулы[править]
где i, j – это индексы небесных тел, а k – номер итерации.
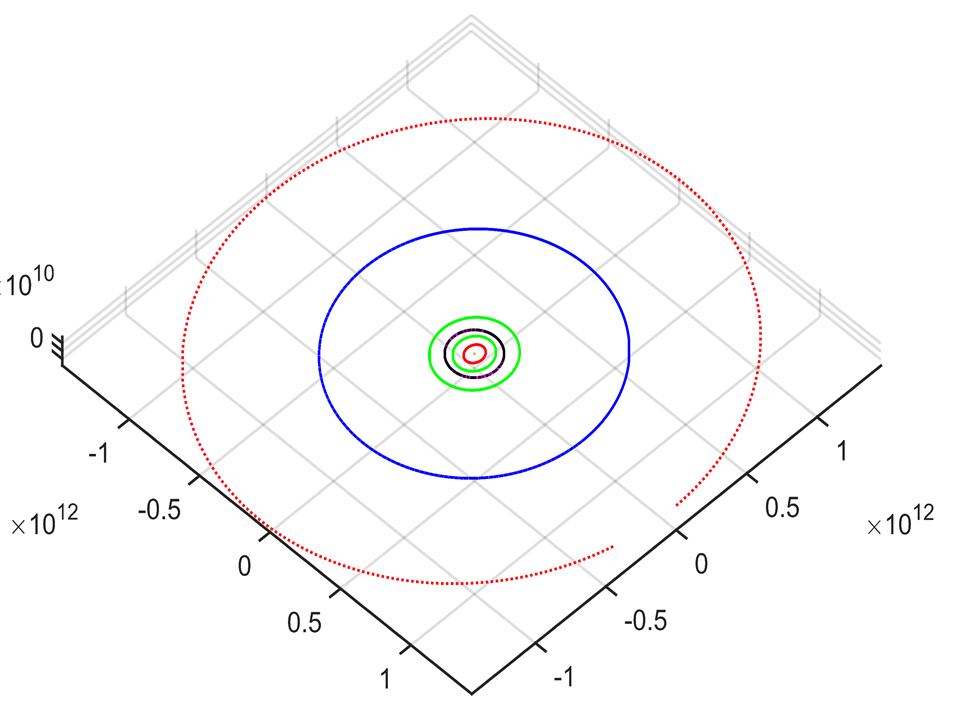
Результаты[править]