Механика дискретных сред и аномальные тепловые процессы — различия между версиями
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
| + | [[А.М. Кривцов: выступления]] > '''Механика дискретных сред и аномальные тепловые процессы.''' <HR> | ||
| + | |||
{{DISPLAYTITLE:<span style="display:none">{{FULLPAGENAME}}</span>}} | {{DISPLAYTITLE:<span style="display:none">{{FULLPAGENAME}}</span>}} | ||
| − | <font size="3">ДОКЛАД "МЕХАНИКА ДИСКРЕТНЫХ СРЕД И АНОМАЛЬНЫЕ ТЕПЛОВЫЕ ПРОЦЕССЫ"</font> | + | <font size="3">ДОКЛАД "МЕХАНИКА ДИСКРЕТНЫХ СРЕД И АНОМАЛЬНЫЕ ТЕПЛОВЫЕ ПРОЦЕССЫ."</font> |
Кривцов Антон Мирославович (СПбПУ, ИПМаш РАН) | Кривцов Антон Мирославович (СПбПУ, ИПМаш РАН) | ||
| + | == Аннотация == | ||
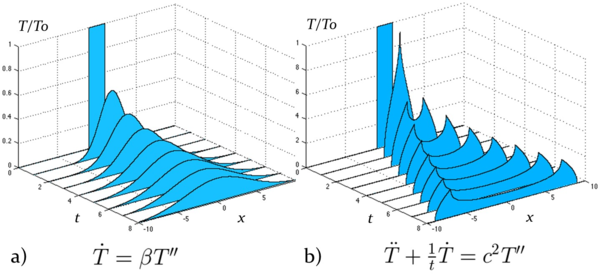
В докладе излагаются подходы и приложения механики дискретных сред. Рассматриваются задачи, в которых проявляется нарушение континуальности среды – или в силу дискретности структуры вещества, или в силу особенности протекающих в нем процессов. Подробно рассматриваются задачи, связанные с описанием аномальных тепловых процессов на микроуровне: немонотонной тепловой релаксации, тепловой сверхпроводимости и др. Предлагаются подходы, позволяющие в простейших случаях на основе уравнений динамики частиц вещества получить аналитическое описание указанных процессов. Проводится сравнение эволюции теплового возмущения при обычной теплопроводности (рис. 1а) и тепловой сверхпроводимости (рис. 1b). Показывается, что тепло в сверхпроводящих системах может распространяться со скоростью, близкой к скорости звука, что открывает возможность для перспективных практических приложений. | В докладе излагаются подходы и приложения механики дискретных сред. Рассматриваются задачи, в которых проявляется нарушение континуальности среды – или в силу дискретности структуры вещества, или в силу особенности протекающих в нем процессов. Подробно рассматриваются задачи, связанные с описанием аномальных тепловых процессов на микроуровне: немонотонной тепловой релаксации, тепловой сверхпроводимости и др. Предлагаются подходы, позволяющие в простейших случаях на основе уравнений динамики частиц вещества получить аналитическое описание указанных процессов. Проводится сравнение эволюции теплового возмущения при обычной теплопроводности (рис. 1а) и тепловой сверхпроводимости (рис. 1b). Показывается, что тепло в сверхпроводящих системах может распространяться со скоростью, близкой к скорости звука, что открывает возможность для перспективных практических приложений. | ||
| + | |||
[[Файл:Sdkhgsdghsd.png|600px|Рисунок 1. Эволюция прямоугольного теплового импульса: a) теплопроводность Фурье, b) тепловая сверхпроводимость.]] | [[Файл:Sdkhgsdghsd.png|600px|Рисунок 1. Эволюция прямоугольного теплового импульса: a) теплопроводность Фурье, b) тепловая сверхпроводимость.]] | ||
| + | |||
| + | == English version == | ||
| + | Methods and applications of mechanics of discrete media are presented. We consider problems where continuity of the media is broken either due to its discrete structure, or due the nature of the occurring processes. The anomalous thermal processes are considered in details: non-monotonic thermal relaxation, thermal superconductivity, and etc. Approaches allowing an analytical description of these processes are presented. It is shown that heat propagation in such systems is performed at a speed close to the speed of sound, which opens possibility for prespective practical applications. | ||
| + | |||
| + | == Литература == | ||
| + | [[А.М. Кривцов]]. '''Распространение тепла в бесконечном одномерном гармоническом кристалле'''. [http://www.maik.ru/cgi-perl/journal.pl?lang=rus&name=dan Доклады Академии Наук]. 2015, том 464, № 2, C. 162-166 ([[Медиа: Krivtsov_2015 DAN rus proof.pdf|pdf]], [[Распространение тепла в гармоническом одномерном кристалле|моделирование]]). English version: [[Krivtsov A. M.]] '''Heat transfer in infinite harmonic one dimensional crystals.''' [http://www.maik.rssi.ru/cgi-perl/journal.pl?name=danphys&page=main Doklady Physics], 2015, Vol. 60, No. 9, pp. 407–411. (Download pdf: [[Медиа: Krivtsov 2015 DAN eng.pdf.pdf|190 Kb]]) | ||
Текущая версия на 10:48, 12 октября 2016
А.М. Кривцов: выступления > Механика дискретных сред и аномальные тепловые процессы.
ДОКЛАД "МЕХАНИКА ДИСКРЕТНЫХ СРЕД И АНОМАЛЬНЫЕ ТЕПЛОВЫЕ ПРОЦЕССЫ."
Кривцов Антон Мирославович (СПбПУ, ИПМаш РАН)
Аннотация[править]
В докладе излагаются подходы и приложения механики дискретных сред. Рассматриваются задачи, в которых проявляется нарушение континуальности среды – или в силу дискретности структуры вещества, или в силу особенности протекающих в нем процессов. Подробно рассматриваются задачи, связанные с описанием аномальных тепловых процессов на микроуровне: немонотонной тепловой релаксации, тепловой сверхпроводимости и др. Предлагаются подходы, позволяющие в простейших случаях на основе уравнений динамики частиц вещества получить аналитическое описание указанных процессов. Проводится сравнение эволюции теплового возмущения при обычной теплопроводности (рис. 1а) и тепловой сверхпроводимости (рис. 1b). Показывается, что тепло в сверхпроводящих системах может распространяться со скоростью, близкой к скорости звука, что открывает возможность для перспективных практических приложений.
English version[править]
Methods and applications of mechanics of discrete media are presented. We consider problems where continuity of the media is broken either due to its discrete structure, or due the nature of the occurring processes. The anomalous thermal processes are considered in details: non-monotonic thermal relaxation, thermal superconductivity, and etc. Approaches allowing an analytical description of these processes are presented. It is shown that heat propagation in such systems is performed at a speed close to the speed of sound, which opens possibility for prespective practical applications.
Литература[править]
А.М. Кривцов. Распространение тепла в бесконечном одномерном гармоническом кристалле. Доклады Академии Наук. 2015, том 464, № 2, C. 162-166 (pdf, моделирование). English version: Krivtsov A. M. Heat transfer in infinite harmonic one dimensional crystals. Doklady Physics, 2015, Vol. 60, No. 9, pp. 407–411. (Download pdf: 190 Kb)