Моделирование фигур Хладни на С++ — различия между версиями
Raisa (обсуждение | вклад) (Новая страница: «Моделирование фигур Хладни на с++ Курсовой проект по информатике Исполнитель: Рубинов…») |
Raisa (обсуждение | вклад) (→Список литературы) |
||
| (не показано 10 промежуточных версий 5 участников) | |||
| Строка 1: | Строка 1: | ||
| − | Моделирование фигур Хладни на с++ | + | '''Моделирование фигур Хладни на с++''' |
Курсовой проект по информатике | Курсовой проект по информатике | ||
| Строка 11: | Строка 11: | ||
| − | ''Аннотация проекта'' | + | ==''Аннотация проекта''== |
| − | Данная курсовая работа посвящена моделированию фигур Хладни при помощи дифференциального уравнения Софи Жермен. Все процессы рассматриваются через механические законы. | + | Данная курсовая работа посвящена моделированию фигур Хладни при помощи дифференциального уравнения Софи Жермен. Все процессы рассматриваются через механические законы, т.е. мы исследуем движение частиц в первую очередь с механической точки зрения: мы представляем, что частицы движутся в результате изгиба пластины под действием силы тяжести. |
| − | |||
| − | 1. Изучить теорию визуализации звуковых полей | + | ==''Постановка задачи''== |
| + | |||
| + | 1. Изучить теорию визуализации звуковых полей | ||
| + | |||
2. Изучить теорию изгиба пластины | 2. Изучить теорию изгиба пластины | ||
| + | |||
3. Написать программу для с++ | 3. Написать программу для с++ | ||
| + | |||
4. Визуализировать полученные данные при помощи gnuplot | 4. Визуализировать полученные данные при помощи gnuplot | ||
| + | |||
| + | |||
| + | ==''Общая информация''== | ||
| + | |||
| + | Фигуры Хладни - фигуры, образуемые скоплением мелких частиц сухого песка вблизи узловых линий на поверхности упругой колеблющейся пластинки или подобной ей механической системы. | ||
| + | Данное явление основано на теории изгиба пластин. | ||
| + | |||
| + | ==''Моделирование''== | ||
| + | |||
| + | В нашей программе мы разбиваем наш процесс на несколько этапов, чтобы облегчить процесс моделирования: сначала мы создаем эллиптическую пластину (задаем ее параметры); на данном этапе мы позволяем пользователю самостоятельно задать параметры, которые он хотел бы увидеть. После этого мы обращаемся к нашему классу, объектом которого является частица: их мы задаем случайным методом, задавая граничные условия: те самые параметры, которые задал пользователь. После этого согласно выведенным формулам высчитываем углы, через которые мы имеем возможность вычислить ускорение частицы по обеим осям. Последним этапом аналитического решения мы вычисляем новые координаты по осям x и y, а также изгиб пластины в конкретной точке. Полученные результаты сохраняются в файл, который мы используем для построения графика. В результате пошагового подхода явление визуализации кажется довольно простым и не очень запутанным. | ||
| + | |||
| + | ==''Результаты моделирования''== | ||
| + | |||
| + | После того как мы получили аналитические результаты (набор точек и их параметров, записанных в файл), мы используем gnuplot для визуализации полученных результатов. | ||
| + | |||
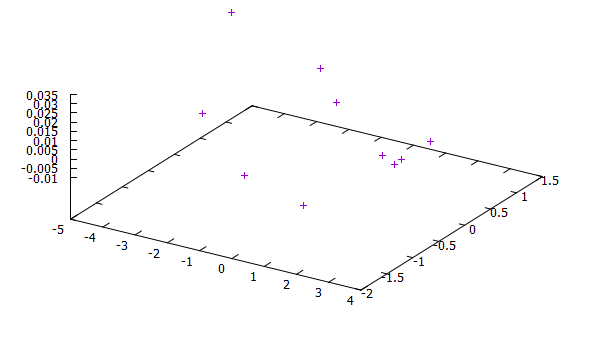
| + | Для наглядности я сделала различные графики. Один из них - точечный, отображающий отдельные точки и их положение. | ||
| + | |||
| + | [[File:график_точ.png]] | ||
| + | |||
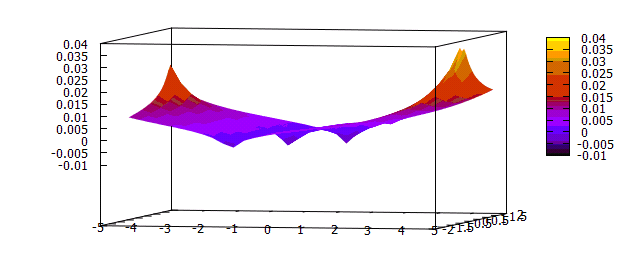
| + | Второй график отображает всю пластину, а не отдельные точки. Так мы получаем более красочную картинку процесса. | ||
| + | |||
| + | [[File:график_пл.png]] | ||
| + | |||
| + | |||
| + | ==''Список литературы''== | ||
| + | |||
| + | 1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика. Классический курс. - М.: Просвещение, 1998. | ||
| + | |||
| + | 2. Кабардин О.Ф. Физика. Справочник материалы. - М.: Просвещение, 1988. | ||
| + | |||
| + | 3. Мякишем Г.Я. Физика. Профильный уровень. - М.: Дрофа, 2012. | ||
| + | |||
| + | 4. Смирнов В.И., Видюшенков С.А. Изгиб пластинок. Учебное пособие. - СПб.: Петербургский гос. ун-т путей сообщения, 2011. | ||
| + | |||
| + | 5. Лафоре Р. Объектно-ориентированное программирование в с++. - СПб.: Питер, 2012. | ||
Общие сведения, а также саму программу можно скачать по ссылке: | Общие сведения, а также саму программу можно скачать по ссылке: | ||
| − | [[:File: | + | [[:File:Kurs_rubinova.rar]] |
Текущая версия на 15:37, 17 июня 2016
Моделирование фигур Хладни на с++
Курсовой проект по информатике
Исполнитель: Рубинова_Раиса
Группа 13604/1 Кафедра Теоретической механики
Семестр: весна 2016
Содержание
Аннотация проекта[править]
Данная курсовая работа посвящена моделированию фигур Хладни при помощи дифференциального уравнения Софи Жермен. Все процессы рассматриваются через механические законы, т.е. мы исследуем движение частиц в первую очередь с механической точки зрения: мы представляем, что частицы движутся в результате изгиба пластины под действием силы тяжести.
Постановка задачи[править]
1. Изучить теорию визуализации звуковых полей
2. Изучить теорию изгиба пластины
3. Написать программу для с++
4. Визуализировать полученные данные при помощи gnuplot
Общая информация[править]
Фигуры Хладни - фигуры, образуемые скоплением мелких частиц сухого песка вблизи узловых линий на поверхности упругой колеблющейся пластинки или подобной ей механической системы. Данное явление основано на теории изгиба пластин.
Моделирование[править]
В нашей программе мы разбиваем наш процесс на несколько этапов, чтобы облегчить процесс моделирования: сначала мы создаем эллиптическую пластину (задаем ее параметры); на данном этапе мы позволяем пользователю самостоятельно задать параметры, которые он хотел бы увидеть. После этого мы обращаемся к нашему классу, объектом которого является частица: их мы задаем случайным методом, задавая граничные условия: те самые параметры, которые задал пользователь. После этого согласно выведенным формулам высчитываем углы, через которые мы имеем возможность вычислить ускорение частицы по обеим осям. Последним этапом аналитического решения мы вычисляем новые координаты по осям x и y, а также изгиб пластины в конкретной точке. Полученные результаты сохраняются в файл, который мы используем для построения графика. В результате пошагового подхода явление визуализации кажется довольно простым и не очень запутанным.
Результаты моделирования[править]
После того как мы получили аналитические результаты (набор точек и их параметров, записанных в файл), мы используем gnuplot для визуализации полученных результатов.
Для наглядности я сделала различные графики. Один из них - точечный, отображающий отдельные точки и их положение.
Второй график отображает всю пластину, а не отдельные точки. Так мы получаем более красочную картинку процесса.
Список литературы[править]
1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика. Классический курс. - М.: Просвещение, 1998.
2. Кабардин О.Ф. Физика. Справочник материалы. - М.: Просвещение, 1988.
3. Мякишем Г.Я. Физика. Профильный уровень. - М.: Дрофа, 2012.
4. Смирнов В.И., Видюшенков С.А. Изгиб пластинок. Учебное пособие. - СПб.: Петербургский гос. ун-т путей сообщения, 2011.
5. Лафоре Р. Объектно-ориентированное программирование в с++. - СПб.: Питер, 2012.
Общие сведения, а также саму программу можно скачать по ссылке: File:Kurs_rubinova.rar