Случайная упаковка шаров — различия между версиями
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 5: | Строка 5: | ||
Рассматривается задача плотной упаковки шаров заданного радиуса в квадрате и круге. Так же в ходе исследования выявляется наиболее плотная 2D упаковка из рассматриваемых. | Рассматривается задача плотной упаковки шаров заданного радиуса в квадрате и круге. Так же в ходе исследования выявляется наиболее плотная 2D упаковка из рассматриваемых. | ||
| − | Программа генерирует последовательно круги разного радиуса в заданной области(квадрат или круг) до тех пор, пока <math> k </math> раз подряд не получим неудачный эксперимент, т.е. наш круг будет задевать другие круги. | + | Программа генерирует последовательно круги разного радиуса в заданной области(квадрат или круг) до тех пор, пока <math> k </math> раз подряд не получим неудачный эксперимент, т.е. в котором наш круг будет задевать другие круги. |
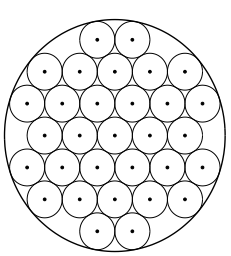
[[Файл:Circles_in_Circle.png]] | [[Файл:Circles_in_Circle.png]] | ||
| Строка 19: | Строка 19: | ||
В верхнем окне рисуется сама упаковка кругов в квадрат или круг, а ниже чертится график зависимости удельного числа проводимых экспериментов(т.е. отношение кол-ва экспериментов с данной плотностью к общему числу экспериментов) от плотности упаковки, которая равна отношению суммарной площади маленьких кругов к площади квадрата/круга. | В верхнем окне рисуется сама упаковка кругов в квадрат или круг, а ниже чертится график зависимости удельного числа проводимых экспериментов(т.е. отношение кол-ва экспериментов с данной плотностью к общему числу экспериментов) от плотности упаковки, которая равна отношению суммарной площади маленьких кругов к площади квадрата/круга. | ||
| + | |||
| + | Экспериментально была вычислена наиболее плотная упаковка кругов в квадрате - при 150 000 экспериментах и <math>a/d</math> = 0.492 вероятность составила 0.76. В круге при 20 000 экспериментах и <math>a/d</math> = 0.292 вероятность была равна 0.68. Соответственно, наиболее плотная упаковка кругов - в квадрате. | ||
{{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/BondarevS/sphere_packing/index.html |width=1250 |height=1200 |border=0 }} | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/BondarevS/sphere_packing/index.html |width=1250 |height=1200 |border=0 }} | ||
Текущая версия на 11:39, 10 мая 2016
Виртуальная лаборатория > Случайная упаковка шаров
Краткое описание[править]
Рассматривается задача плотной упаковки шаров заданного радиуса в квадрате и круге. Так же в ходе исследования выявляется наиболее плотная 2D упаковка из рассматриваемых.
Программа генерирует последовательно круги разного радиуса в заданной области(квадрат или круг) до тех пор, пока раз подряд не получим неудачный эксперимент, т.е. в котором наш круг будет задевать другие круги.
Для работы программы[править]
Для запуска программы выберите, какой эксперимент хотите провести - случайная упаковка в квадрате ( кнопка "square") или в круге (кнопка "circle") и нажмите "Start".
Так же мы можем варьировать отношение диаметра маленького кружка к стороне квадрата/диаметру большого круга и количество экспериментов - и кол-во "неудачных" экспериментов , если будем двигать ползунок или задавать значение в специально отведённом окошке.
"min плотность" показывает наименьшее значение плотной упаковки для данного количества экспериментов и данного заданного числа "неудачных" экспериментов, "avg плотность" - наиболее вероятная упаковка, а "max плотность" - наиболее плотная упаковка.
В верхнем окне рисуется сама упаковка кругов в квадрат или круг, а ниже чертится график зависимости удельного числа проводимых экспериментов(т.е. отношение кол-ва экспериментов с данной плотностью к общему числу экспериментов) от плотности упаковки, которая равна отношению суммарной площади маленьких кругов к площади квадрата/круга.
Экспериментально была вычислена наиболее плотная упаковка кругов в квадрате - при 150 000 экспериментах и = 0.492 вероятность составила 0.76. В круге при 20 000 экспериментах и = 0.292 вероятность была равна 0.68. Соответственно, наиболее плотная упаковка кругов - в квадрате.
Скачать Tight packing.rar.
Текст программы на языке Dart (разработчик Бондарев Сергей):