Определение модулей жесткости прямолинейных стержней. — различия между версиями
Анастасия (обсуждение | вклад) (Новая страница: «''Автор работы'': Прокопенко Анастасия <br> ''Научный руководитель'': к. ф.-м. н. Вильчевская Е.…») |
Анастасия (обсуждение | вклад) |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 4: | Строка 4: | ||
= Введение = | = Введение = | ||
Теория стержней сыграла большую роль в развитии механики и математической физики. Именно в этой теории впервые возникли дифференциальные уравнения, как обыкновенные, так и в частных производных. | Теория стержней сыграла большую роль в развитии механики и математической физики. Именно в этой теории впервые возникли дифференциальные уравнения, как обыкновенные, так и в частных производных. | ||
| + | |||
В механике сплошных сред, которая описывается уравнениями в частных производных, в которых в качестве независимых переменных выступают три пространственных координаты и время. А в теории стержней фигурируют всего две независимых переменных: одна пространственная координата (обычно длина дуги упругой линии), а второй координатой является время. Получается, что наличие одной пространственной координаты сильно упрощает ситуацию, и именно в теории стержней оказывается возможным исследовать пространственные формы движения. | В механике сплошных сред, которая описывается уравнениями в частных производных, в которых в качестве независимых переменных выступают три пространственных координаты и время. А в теории стержней фигурируют всего две независимых переменных: одна пространственная координата (обычно длина дуги упругой линии), а второй координатой является время. Получается, что наличие одной пространственной координаты сильно упрощает ситуацию, и именно в теории стержней оказывается возможным исследовать пространственные формы движения. | ||
| + | |||
Важно заметить, что тонкий стержень при малых деформациях допускает большие перемещения. Например, изначально прямой стержень можно свернуть в кольцо, при этом деформации стержня останутся пренебрежимо малыми. | Важно заметить, что тонкий стержень при малых деформациях допускает большие перемещения. Например, изначально прямой стержень можно свернуть в кольцо, при этом деформации стержня останутся пренебрежимо малыми. | ||
| − | + | ||
| + | Существует два метода вывода основных уравнений тонких стержней: асимптотический и прямой. Асимптотический метод основан на уравнениях трехмерной теории и ряде априорных предположений относительно внутренней структуры стержня и характера поведения решения. Прямой метод основан на непосредственном использовании фундаментальных законов механики. Этот метод имеет более широкую область применимости, поскольку при выводе основных уравнений не делается никаких предположений о характере поведения решения, а все особенности внутренней структуры стержня содержатся в тензорах жесткости. В данной работе рассматривается прямой метод. | ||
= Цели данной работы = | = Цели данной работы = | ||
| Строка 21: | Строка 24: | ||
<math>\rho_{0}\left(\underline{u}\cdot\underline{\underline{\Theta_{1}}}+\underline{\underline{\Theta_{2}}}\cdot\underline{\psi}\right)=\int\rho\underline{a}\times \underline{u_{3}}dxdy</math> | <math>\rho_{0}\left(\underline{u}\cdot\underline{\underline{\Theta_{1}}}+\underline{\underline{\Theta_{2}}}\cdot\underline{\psi}\right)=\int\rho\underline{a}\times \underline{u_{3}}dxdy</math> | ||
| − | [[Файл:free.jpg| | + | [[Файл:free.jpg|200px|thumb|right|Рис 1. Стержень со свободным концом]] |
| − | [[Файл:nofree.jpg| | + | [[Файл:nofree.jpg|200px|thumb|right|Рис 2. Стержень с заделками с двух сторон]] |
= Нахождение модуля жесткости при поперечном сдвиге = | = Нахождение модуля жесткости при поперечном сдвиге = | ||
| Строка 30: | Строка 33: | ||
В изогнутом стержне в некоторых местах его происходит растяжение, а в других — сжатие. Растянуты линии на выпуклой стороне изогнутого стержня, а на вогнутой стороне происходит сжатие. Как и в случае пластинок, вдоль длины стержня внутри него существует «нейтральная» поверхность, на которой не происходит ни растяжения, ни сжатия. Она отделяет собой области сжатия от областей растяжения. | В изогнутом стержне в некоторых местах его происходит растяжение, а в других — сжатие. Растянуты линии на выпуклой стороне изогнутого стержня, а на вогнутой стороне происходит сжатие. Как и в случае пластинок, вдоль длины стержня внутри него существует «нейтральная» поверхность, на которой не происходит ни растяжения, ни сжатия. Она отделяет собой области сжатия от областей растяжения. | ||
В этой задачи будет две компоненты модуля упругости: на сдвиг и на растяжение. При решении этой задачи нужно раскрыть векторное произведение (см. формула из метода решения). Из-за большого количества узлов погрешность будет большой. Чтобы избежать эту проблему нужно решить две задачи: сдвиг стержня со свободным концом (Рис. 1) и с заделкой, как показано на Рис 2. | В этой задачи будет две компоненты модуля упругости: на сдвиг и на растяжение. При решении этой задачи нужно раскрыть векторное произведение (см. формула из метода решения). Из-за большого количества узлов погрешность будет большой. Чтобы избежать эту проблему нужно решить две задачи: сдвиг стержня со свободным концом (Рис. 1) и с заделкой, как показано на Рис 2. | ||
| + | |||
| + | Угол закручивания в первом случае будет равен: | ||
| + | |||
| + | <math>\underline{\psi _{1}}= \frac{N_{0}}{C_{x}}z\left ( l-\frac{z}{2} \right )\underline{i} </math> | ||
| + | |||
| + | Угол закручивания для стержня с двумя заделками: | ||
| + | |||
| + | <math>\underline{\psi _{2}}= \frac{N_{0}}{C_{x}}\frac{z}{2}\left ( z-l \right )\underline{i} </math> | ||
| + | |||
| + | Выражаем в обоих случаях перемещение, будем иметь соответственно: | ||
| + | |||
| + | <math>u_{1}= -\frac{N_{0}}{A_{y}}z-\frac{N_{0}}{2C_{x}}\left ( z^{2}l-\frac{z^{3}}{3} \right ) </math> | ||
| + | |||
| + | <math>u_{2}= -\frac{N_{0}}{A_{y}}z-\frac{N_{0}}{2C_{x}}\left ( \frac{z^{2}l}{2}-\frac{z^{3}}{3} \right )</math> | ||
| + | |||
| + | Где <math>u_{1}</math> - перемещение стержня со свободным концом, а <math>u_{2}</math> - с заделкой с двух сторон, <math>A_{y}</math> - модуль жесткости на поперечный сдвиг, <math>C_{x}</math> - модуль жесткости на кручение. | ||
| + | Переходим к относительной координате сечения, делая замену <math>r=zl</math>. | ||
| + | Получаем итоговую формулу для модуля жесткости на поперечный сдвиг: | ||
| + | |||
| + | <math>A_{y}=\frac{3rlN_{0}}{u_{1}\left(3-2r\right)-2u_{2}\left(3-r\right)}</math> | ||
| + | |||
| + | = Коэффициент сдвига = | ||
| + | Для нахождения коэффициента сдвига, понадобиться следующая формула: <math>k=\frac{A_{y}}{GS}</math>, где <math>G</math> - модуль сдвига, <math>S</math> - площадь поперечного сечения. | ||
| + | Были предложены различные искусственные приемы отыскания корректирующего коэффициента k в уточненных теориях, основанных на сдвиговой модели Тимошенко. Все эти приемы являются приближенными. При построении уточненных уравнений, как математических аппроксимаций краевой задачи динамической теории упругости, не требуется введения каких–либо искусственных величин. Поэтому из сравнения математических аппроксимаций с соответствующими уточненными теориями, содержащими искусственные величины, можно найти формулы для корректирующих коэффициентов, иногда в явном виде. Отобразим такие величины на графике для сравнения с величиной, полученной по нашей формуле. | ||
| + | |||
| + | [[Файл:kofK.jpg | Рис 3. Зависимость коэффициента сдвига от коэффициента Пуассона]] | ||
| + | Рис 3. Зависимость коэффициента сдвига от коэффициента Пуассона | ||
| + | |||
| + | = Влияние формы сечения на модуль жесткости на поперечный сдвиг = | ||
| + | [[Файл:forma.jpg | Рис 4. Формы поперечного сечения]] | ||
| + | Рис 4. Формы поперечного сечения | ||
| + | |||
| + | В этом случае полученные значения модуля жесткости на поперечный сдвиг при разных формах сечения можно представить в виде гистограммы (Рис 5.): | ||
| + | |||
| + | [[Файл:gisto.jpg | Рис 5. Влияние формы сечения на модуль поперечного сдвига]] | ||
| + | Рис 5. Влияние формы сечения на модуль поперечного сдвига | ||
| + | |||
| + | |||
| + | Получается, что модуль жесткости на поперечный сдвиг при разных формах сечения имеет разные значения. Связано это с тем, что, если в случае растяжения стержня был один модуль жесткости на растяжении, то в случае изгиба стержня будет уже два модуля жесткости: один на растяжение, другой на изгиб. | ||
| + | |||
| + | = Анализ модуля жесткости на поперечный сдвиг = | ||
| + | При моделировании рассматривается задача об изгибе стержня длиной. Площадь сечения является постоянной величиной для разных форм сечений, площадь отверстий также постоянная величина. | ||
| + | |||
| + | [[Файл:ankof.jpg | Рис 6. Влияние формы сечения на модуль поперечного сдвига]] | ||
| + | Рис 6. Численные значения модуля жёсткости при разных формах сечения | ||
| + | |||
| + | По представленным значениям на Рис 6., сделаем вывод о том, как влияет расположение сквозных отверстий на модуль жесткости на поперечный сдвиг. | ||
| + | Во-первых, при увеличении числа сквозных отверстий, когда площадь отверстий не меняется, модуль сдвига будет значительно уменьшаться. | ||
| + | Во-вторых, при удалении от центра сквозных отверстий, модуль сдвига также будет уменьшаться. | ||
| + | |||
| + | |||
| + | = Выводы = | ||
| + | Используя предложенный П.А. Жилиным статический метод | ||
| + | определения модулей упругости тонкостенных конструкций, были найдены модули сдвига стержней, различной формы поперечного сечения. И был найден модули жесткости для квадратной формы поперечного сечения со сквозными отверстиями. | ||
| + | |||
| + | В работе решен ряд тестовых задач о статическом деформировании по теории стержней. Тестовые задачи выбирались таким образом, чтобы решение каждой из них содержало бы только один неизвестный модуль упругости. Затем те же задачи были решены численным методом по трехмерной теории. Основываясь на сравнении напряженно-деформированного состояния стержней и трехмерных тел, были найдены корректирующие коэффициенты сдвига. Полученные величины имеют схожие значения с корректирующими коэффициентами сдвига, полученными на основании других методов. | ||
| + | |||
| + | Также удалось систематизировать данные и сделать вывод о влиянии расположения сквозных отверстий на модуль жесткости при поперечном сдвиге. А именно: при увеличении у стержня числа отверстий и при удалении их от центра, модуль сдвига будет значительно уменьшаться. | ||
| + | |||
| + | = Литература = | ||
| + | *Феодосьев В. И. Сопротивление материалов. — М.: изд-во МГТУ им.Н. Э. Баумана, 1999 | ||
| + | *Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. В 10-ти т. Т. VII. Теория упругости: Учеб. пособие. — 4-е изд., испр. и доп. — М.; Наука. Гл. ред. физ.-мат. лит., 1987. — 248 с. | ||
| + | *Э. И. Григолюк, И. Т. Селезов. Механика твердых деформируемых тел. Том 5. Неклассические теории колебаний стержней, пластин и оболочек. | ||
| + | *П. А. Жилин. Прикладная механика. Теория тонких упругих стержней. | ||
Текущая версия на 15:04, 30 ноября 2015
Автор работы: Прокопенко Анастасия
Научный руководитель: к. ф.-м. н. Вильчевская Е.Н.
Содержание
Введение[править]
Теория стержней сыграла большую роль в развитии механики и математической физики. Именно в этой теории впервые возникли дифференциальные уравнения, как обыкновенные, так и в частных производных.
В механике сплошных сред, которая описывается уравнениями в частных производных, в которых в качестве независимых переменных выступают три пространственных координаты и время. А в теории стержней фигурируют всего две независимых переменных: одна пространственная координата (обычно длина дуги упругой линии), а второй координатой является время. Получается, что наличие одной пространственной координаты сильно упрощает ситуацию, и именно в теории стержней оказывается возможным исследовать пространственные формы движения.
Важно заметить, что тонкий стержень при малых деформациях допускает большие перемещения. Например, изначально прямой стержень можно свернуть в кольцо, при этом деформации стержня останутся пренебрежимо малыми.
Существует два метода вывода основных уравнений тонких стержней: асимптотический и прямой. Асимптотический метод основан на уравнениях трехмерной теории и ряде априорных предположений относительно внутренней структуры стержня и характера поведения решения. Прямой метод основан на непосредственном использовании фундаментальных законов механики. Этот метод имеет более широкую область применимости, поскольку при выводе основных уравнений не делается никаких предположений о характере поведения решения, а все особенности внутренней структуры стержня содержатся в тензорах жесткости. В данной работе рассматривается прямой метод.
Цели данной работы[править]
- Определить модули жесткости прямолинейных стержней на основании численного эксперимента
- Исследовать влияние количества сквозных отверстий на модуль жесткости на поперечный сдвиг
Постановка задачи: метод решения[править]
Тензоры жесткости не зависят от деформации, поэтому они могут быть определены по данным линейной теории. Модули упругости будем находить при помощи статического метода. Суть это метода заключается в следующем: решается задача о статическом деформировании по теории стержней, в результате чего находятся перемещения и повороты. Затем та же задача решается по трехмерной теории, либо проводится физический эксперимент, в результате которого также находятся деформации. Важный момент статического метода определения модулей упругости является выбор формул, связывающих между собой характеристики состояния трехмерного тела и состояние соответствующей модели стержня.
Стержень – это модель тонкого трёхмерного тела. Потребуем, чтобы количество движения и кинетический момент у модели и у трёхмерного тела (прообраза) совпадали бы между собой. В результат придём к следующим уравнениям (для линейной теории):
Нахождение модуля жесткости при поперечном сдвиге[править]
Испытания на сдвиг часто используются для оценки механических свойств материалов в хрупком или малопластичном состоянии, при воздействии коррозионной среды (коррозии под напряжением), а также для оценки пластичности и качества сварных соединений. Испытание на сдвиг воспроизводит характерные для многих конструктивных элементов условия механического нагружения и позволяет выявить свойства поверхностных слоев, наиболее напряженных при разрушении.
В изогнутом стержне в некоторых местах его происходит растяжение, а в других — сжатие. Растянуты линии на выпуклой стороне изогнутого стержня, а на вогнутой стороне происходит сжатие. Как и в случае пластинок, вдоль длины стержня внутри него существует «нейтральная» поверхность, на которой не происходит ни растяжения, ни сжатия. Она отделяет собой области сжатия от областей растяжения. В этой задачи будет две компоненты модуля упругости: на сдвиг и на растяжение. При решении этой задачи нужно раскрыть векторное произведение (см. формула из метода решения). Из-за большого количества узлов погрешность будет большой. Чтобы избежать эту проблему нужно решить две задачи: сдвиг стержня со свободным концом (Рис. 1) и с заделкой, как показано на Рис 2.
Угол закручивания в первом случае будет равен:
Угол закручивания для стержня с двумя заделками:
Выражаем в обоих случаях перемещение, будем иметь соответственно:
Где - перемещение стержня со свободным концом, а - с заделкой с двух сторон, - модуль жесткости на поперечный сдвиг, - модуль жесткости на кручение. Переходим к относительной координате сечения, делая замену . Получаем итоговую формулу для модуля жесткости на поперечный сдвиг:
Коэффициент сдвига[править]
Для нахождения коэффициента сдвига, понадобиться следующая формула: , где - модуль сдвига, - площадь поперечного сечения. Были предложены различные искусственные приемы отыскания корректирующего коэффициента k в уточненных теориях, основанных на сдвиговой модели Тимошенко. Все эти приемы являются приближенными. При построении уточненных уравнений, как математических аппроксимаций краевой задачи динамической теории упругости, не требуется введения каких–либо искусственных величин. Поэтому из сравнения математических аппроксимаций с соответствующими уточненными теориями, содержащими искусственные величины, можно найти формулы для корректирующих коэффициентов, иногда в явном виде. Отобразим такие величины на графике для сравнения с величиной, полученной по нашей формуле.
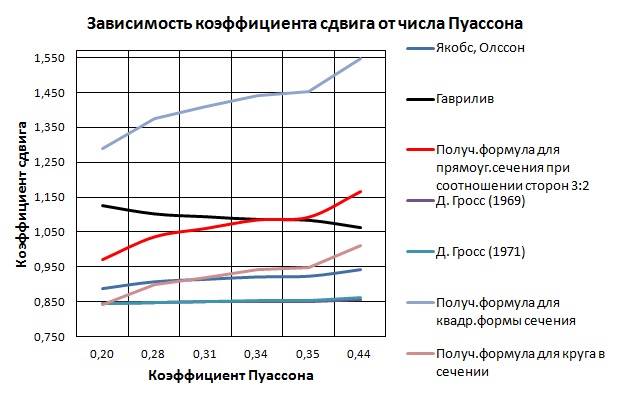 Рис 3. Зависимость коэффициента сдвига от коэффициента Пуассона
Рис 3. Зависимость коэффициента сдвига от коэффициента Пуассона
Влияние формы сечения на модуль жесткости на поперечный сдвиг[править]
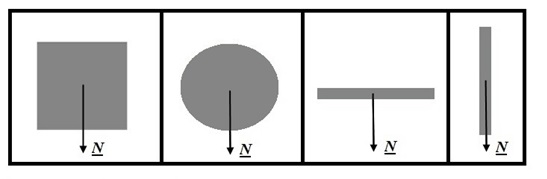 Рис 4. Формы поперечного сечения
Рис 4. Формы поперечного сечения
В этом случае полученные значения модуля жесткости на поперечный сдвиг при разных формах сечения можно представить в виде гистограммы (Рис 5.):
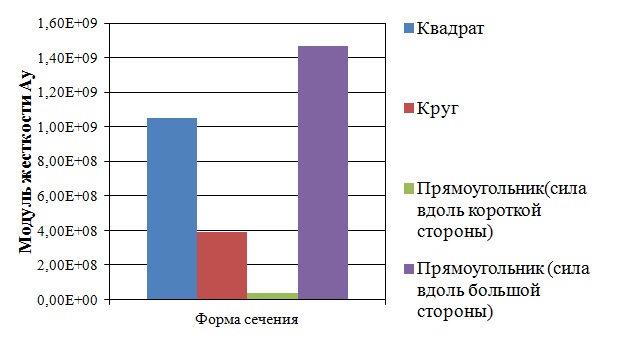 Рис 5. Влияние формы сечения на модуль поперечного сдвига
Рис 5. Влияние формы сечения на модуль поперечного сдвига
Получается, что модуль жесткости на поперечный сдвиг при разных формах сечения имеет разные значения. Связано это с тем, что, если в случае растяжения стержня был один модуль жесткости на растяжении, то в случае изгиба стержня будет уже два модуля жесткости: один на растяжение, другой на изгиб.
Анализ модуля жесткости на поперечный сдвиг[править]
При моделировании рассматривается задача об изгибе стержня длиной. Площадь сечения является постоянной величиной для разных форм сечений, площадь отверстий также постоянная величина.
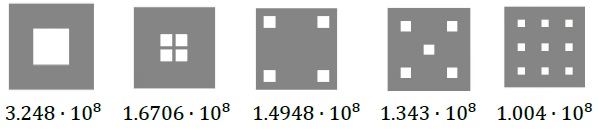 Рис 6. Численные значения модуля жёсткости при разных формах сечения
Рис 6. Численные значения модуля жёсткости при разных формах сечения
По представленным значениям на Рис 6., сделаем вывод о том, как влияет расположение сквозных отверстий на модуль жесткости на поперечный сдвиг. Во-первых, при увеличении числа сквозных отверстий, когда площадь отверстий не меняется, модуль сдвига будет значительно уменьшаться. Во-вторых, при удалении от центра сквозных отверстий, модуль сдвига также будет уменьшаться.
Выводы[править]
Используя предложенный П.А. Жилиным статический метод определения модулей упругости тонкостенных конструкций, были найдены модули сдвига стержней, различной формы поперечного сечения. И был найден модули жесткости для квадратной формы поперечного сечения со сквозными отверстиями.
В работе решен ряд тестовых задач о статическом деформировании по теории стержней. Тестовые задачи выбирались таким образом, чтобы решение каждой из них содержало бы только один неизвестный модуль упругости. Затем те же задачи были решены численным методом по трехмерной теории. Основываясь на сравнении напряженно-деформированного состояния стержней и трехмерных тел, были найдены корректирующие коэффициенты сдвига. Полученные величины имеют схожие значения с корректирующими коэффициентами сдвига, полученными на основании других методов.
Также удалось систематизировать данные и сделать вывод о влиянии расположения сквозных отверстий на модуль жесткости при поперечном сдвиге. А именно: при увеличении у стержня числа отверстий и при удалении их от центра, модуль сдвига будет значительно уменьшаться.
Литература[править]
- Феодосьев В. И. Сопротивление материалов. — М.: изд-во МГТУ им.Н. Э. Баумана, 1999
- Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. В 10-ти т. Т. VII. Теория упругости: Учеб. пособие. — 4-е изд., испр. и доп. — М.; Наука. Гл. ред. физ.-мат. лит., 1987. — 248 с.
- Э. И. Григолюк, И. Т. Селезов. Механика твердых деформируемых тел. Том 5. Неклассические теории колебаний стержней, пластин и оболочек.
- П. А. Жилин. Прикладная механика. Теория тонких упругих стержней.