Идентификация параметров пороупругой среды на примере бетонной плотины — различия между версиями

Текущая версия на 13:32, 22 октября 2015

БАКАЛАВРСКАЯ РАБОТА
Автор работы: Р. Л. Лапин
Руководитель: ассистент кафедры ТМ С. А. Ле-Захаров

Введение[править]

На сегодняшний моделей позволяющих просто и качественно описывать поведения материалов, имеющих в своем строении трещины и швы, в которых может находится газ или жидкость нет. Однако, необходимость в такой модели есть во многих технических областях. Ярким примером является анализ поведения плотины и грунта под ней под действием внешних факторов, например, воды в водохранилище.

Постановка задачи[править]

Для материалов пористой структуры существует несколько моделей, например известные модели грунтов. Однако применимость их к материалам имеющих в своем строении трещины и швы остается под вопросом. Цель данной работы:

• Построить на базе модели пористой среды модель для бетона
• Провести сравнение с экспериментальными данными
• Проанализировать полученные результаты.

Обработка экспериментальных данных[править]

Расположения датчиков. Вид сверху

Показания датчиков соответствующие p=0.98

Показания датчиков соответствующие p=0.03

Пример линейной регрессионной модели

Пример квадратичной регрессионной модели

Экспериментальные основаны на данных полученных с датчиков, расположенным в Саяно-Шушенской ГЭС. Датчики-пьезометры, измеряющие давление. Всего датчиков около 140, данные собираются с регулярностью 3-5 раза в месяц на протяжении последних 15 лет. Обработка данных с датчиков разделяется на два этапа: корреляционный анализ, и регрессионный анализ.

Корреляционный анализ[править]

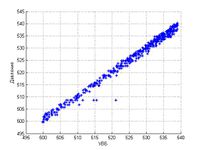
Корреляционный анализ позволяет определить зависит по набору данных зависит ли одна величина от другой. В ходе работы было выяснено, что разумнее всего исследовать зависимость показаний пьезометров от уровня воды в верхнем водохранилище - УВБ. Характеристикой зависимости был выбран коэффициент корреляции Спирмена.

[math] p \ = 1 - 6\frac{\sum{d}}{n^3-n}, p \in [-1; 1][/math]

Где [math]d[/math] - разность рангов величин взятых по одному из наборов данных для которых применяется анализ.

Значения коэффициента Спирмена близкое по модулю к [math]1[/math] говорит о том, что две величины зависят друг от друга. Значение близкое к [math]0[/math] говорит о независимости величин.

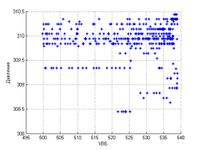
По результатам анализа был проведен отбор датчиков, которые можно считать хорошо работающими.

Регрессионный анализ[править]

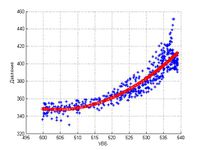
Для датчиков, которые удовлетворили корреляционному анализу была найдена модель зависимости показаний от УВБ. Метод решения этйо задачи регрессионный анализ.

Его идея в том, что для набора величин [math](X; Y)[/math] составляется предположительный вид зависимости, в данной работе полиномиальный [math]\bar{y} = a_0x^n+a_1x^{n-1}+...a_{n-1}x+a_n[/math]. Затем, для нахождения неизвестных коэффициентов [math]a_i[/math] используется метод наименьших квадратов. Строится функционал невязки [math] I= \sum{(\bar{y}(x_i)-y_i})[/math]. От которого беруться производные от [math]a_i[/math] и приравниваются к [math]0[/math]. В итоге получается линейная [math]n[/math]-мерная система относительно [math]n[/math] неизвестных, из которой находятся коэффициенты [math]a_i[/math].

В данной работе использовался линейный и квадратичный вид зависимости.

Модель материала[править]

Модель материала, имеющего в структуре трещины, основана на модели пороупругого материала. Опишем систему уравнений, задающих модель.

Одним из уравнений является уравнение равновесия: [math]\nabla\cdot\boldsymbol{\sigma} = 0[/math]

Тензор напряжений расписывается согласно принципу эффективных напряжений:

[math]\boldsymbol{\sigma} = (1-m)\boldsymbol{\sigma^*}+m(sp_ж+(1-s)p_г)\boldsymbol{E}[/math]

Где [math]\boldsymbol{\sigma^*}[/math] - напряжения в скелете материла, которые подчиняются линейной теории упругости; [math]m[/math] - пористость материала; [math]s[/math] - сатурация материала.

На первоначальном этапе считается, что материал обладает стопроцентной сатурацией, то есть [math]s = 1[/math]. Тогда тензор напряжений принимает вид:

[math]\boldsymbol{\sigma} = (1-m)\boldsymbol{\sigma^*}+mp_ж\boldsymbol{E}[/math]

Для описания движения жидкости в материале используется закон Дарси:

[math]\bar{w} = -k_*grad(p_ж)[/math]

Где[math]k_*[/math] коэффициент проводимости материала.

Последним уравнением, замыкающим систему является уравнение неразрывности:

[math] div(\rho\bar{w})=0[/math]

Эти уравнения образуют систему относительно [math]\boldsymbol{\sigma^*}, p_ж[/math].

Результаты моделирования[править]

Напряжения при третьей постановке

Пьезометрическое давление при третьей постановке

Эпюры поровых давлений для разных постановок с глубине 1 метр

В ходе моделирования решалась статическая задача, так же заметим что модель двумерная. Моделирование происходило в трех различных постановках

• Без учета УНБ
• С учетом УНБ
• С учетом УНБ и противофильтрационной завесы

Наличие нескольких постановок связано с тем, что в начале исследования не было понятно какие параметры влияют на результат.

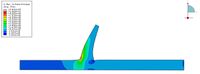
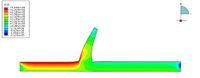
В результате моделирования полученным поля напряжений, перемещений и пьезометрического давления для всех трех постановок.

Наиболее интересной зоной при моделировании был зона на расстоянии 1 метр от уровня земли. Эта зоня ялвляется зоной наиболее большого количества датчиков, а так же потому что она является стыком двух типов материалов - бетона и грунта.

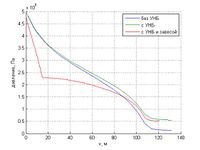
В результате работы исследовано распределение порового давление на этой глубине вдоль оси параллельной земле. Наблюдается уменьшение давление с движением от УВБ. Так же нужно заметить, что противофильтрационная завеса создает резкое понижение порового давления. Отметим, что в удалении от стенки графики практически совпадают.

Сравнение результатов модели с результатами эксперимента[править]

Анализ датчиков, расположенных на одинаковом расстоянии от центра кривизны плотины[править]

Сравнение модели и эксперемента

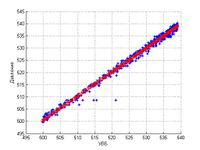
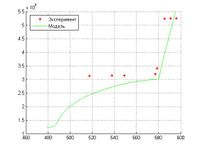
Для сравнения результатов моделирования и натурных данных использовались показания датчиков для 33 секции плотины Саяно-Шушенской ГЭС. При сравнении показаний и результатов моделирования в третьей постановке выяснилось, что модель количественно и качественно совпадает с натурными данными.

Выводы[править]

В ходе работы были решены сразу несколько задач:

1) Обработаны экспериментальные данные датчиков в плотине. Реализована схема отсеивания датчиков показывающие неразумные значения. А на показаниях хорошо работающих датчиков построены модели зависимостей порового давления от уровня УВБ.

2) Реализована модель пороупругого материала для бетона в вычислительном пакете SIMULIA ABAQUS. Получены результаты для различных постановок задачи. Проведено сравнение результатов от постановки задачи. Исследована зависимость порового давления от УВБ.

3) Исследовано влияние угловой координаты на показания датчиков. Определено, что на показания влияет лишь высота расположения датчика и расстояние до центра кривизны плотины.

4) Проведено сравнение исследуемой модели и экспериментальных данных для 33 секции плотины.

По результатам данной работы можно сделать несколько выводов.

Во-первых, для сравнения результатов моделирования и реального материала в исследуемой плотине находится недостаточное количество датчиков. Так же возникает проблема, что находящиеся в плотине датчики расположены группами, но не по всему телу плотины, а лишь в определённых областях. Отсюда возникает затруднения при анализе эксперимента и сравнении его с результатами моделирования, так что делать каких-то уверенных выводов нельзя. Для полной уверенности нужно либо больше датчиков, либо сравнение моделирования и эксперимента нужно проводить по показаниям других групп датчиков, например, расходометрам, наклономеров, деформометров. Кроме того, можно пользоваться лабораторным экспериментом, выполненным с керном, изъятым из тела плотины, и моделированием этого лабораторного эксперимента. Это одно из направлений дальнейшего исследования.

Во-вторых, данная модель согласуется с экспериментом. Особенно хорошо, она описывает область вблизи противофильтрационной завесы плотины. Здесь наблюдается количественное и качественное совпадение. Но имеются расхождения в отдалении от нее. Одним из вариантов доработки модели является более точное описание материала бетона. Например, замена постоянной пористости, на некую функции зависящую от различных параметров: координаты, напряжения, температуры и так далее. Еще одним из направлений развития является оценка напряженно – деформированного состояния сооружений под действием землетрясения с учетом рассмотренных факторов, в том числе влияния поровой жидкости. Особый интерес данной проблемой, вызван появлением во время землетрясения новых трещин в сооружении и фильтрации жидкости в них изменения свойств и параметров сооружений. Реализация этих направлений является дальнейшим планом развития работы.

Материалы работы[править]

• Презентация работы(pdf)
• Превью(pdf)
• Плакат(pdf)

Литература[править]

• К.С. Басниев, А.М. Власов, И.Н. Кочина, В.М. Максимов. Подземная гидравлика. Учебник для ВУЗов – 1986г. 306 с.
• J.F. Shao, Y. Jia, D. Kondo, A.S. Chiarelli. A coupled elastoplastic damage model for semi-brittle materials and extension to unsaturated conditions – 2004г.
• М.Н.Ваучский, Ю.В.Добрица, А.П.Смирнов О.И.Канинский К вопросу о фильтрационных характеристиках бетона – 1998г.
• Н.А. Вульфович, Л.А. Гордон, Н.И. Стефаненко. Арочно-гравитационная плотина Саяно – Шушенской ГЭС. Оценка технического состояния по данным натурных наблюдений – 2012г.
• Е.Л. Косарев. Методы обработки экспериментальных данных – М.: ФИЗМАЛИТ – 2008, 208 с.
• Айвазян С.А., Мхитарян В.С. Теория вероятностей и прикладная статистика – М.: ЮНИТИ-ЛАНА – 2001г. 656 с.
• Дрейпер Н., Смит Г. Прикладной регрессионный анализ: В 2-х кн. Кн. 1 / Пер. с англ. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 1986г.– 366 с.
• M. A. Blot General Theory of Three-Dimensional Consolidation – 1940 г.
• Alan W. Bishop. The principle of the effective stress – 1960г.
• Clayton, C.R.I., Steinhagen, Muller, Steinhagin, H.M., Powrie, W., Terzaghi, K. and Skempton, A.W. Terzaghi's theory of consolidation and the discovery of effective stress. (Compiled from the work of K. Trzaghi and A.W. Skempton). Proceedings of the ICE - Geotechnical Engineering, 113, (4) – 1995г., 191-205.
• Simulia Abaqus Theory Manual 6.11 – 2011г.
• Г. Стренг, Дж. Фикс - Теория метода конечных элементов – 1973 г.