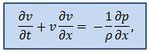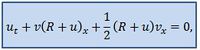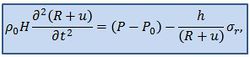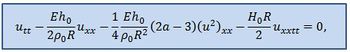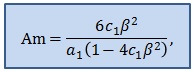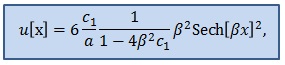Динамическое исследование аневризмы аорты — различия между версиями
(Новая страница: «== Руководитель == проф. дфмн. А.В. Порубов == Введение == Аорта – самый крупный артериальны…») |
|||
| (не показаны 4 промежуточные версии этого же участника) | |||
| Строка 4: | Строка 4: | ||
Аорта – самый крупный артериальный сосуд в теле человека, от которого отходят все артерии, образующие большой круг кровообращения. | Аорта – самый крупный артериальный сосуд в теле человека, от которого отходят все артерии, образующие большой круг кровообращения. | ||
| − | С аортой связано множество заболеваний. Аневризма аорты – расширение участка аорты, обусловленное патологическим изменением соединительно-тканных структур ее стенок вследствие атеросклеротического процесса, воспалительного поражения, врожденной неполноценности или механических повреждений артериальной стенки | + | С аортой связано множество заболеваний. Аневризма аорты – расширение участка аорты, обусловленное патологическим изменением соединительно-тканных структур ее стенок вследствие атеросклеротического процесса, воспалительного поражения, врожденной неполноценности или механических повреждений артериальной стенки. |
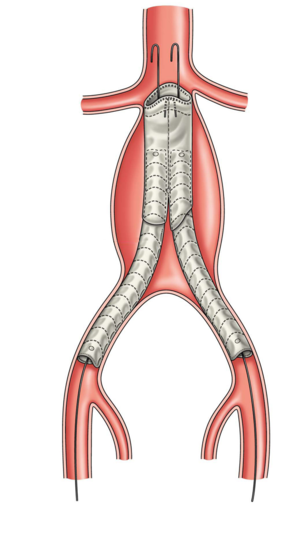
[[Файл:66518_html_m31bb26e5.png|300px|thumb|right|Стентирование аорты]] | [[Файл:66518_html_m31bb26e5.png|300px|thumb|right|Стентирование аорты]] | ||
| − | Для лечения заболеваний сердечно-сосудистой системы хирурги часто используют некоторые искусственные материалы, такие как стенты и протезы. Стент — специальная, изготовленная в форме цилиндрического каркаса упругая металлическая или пластиковая конструкция, которая помещается в просвет полых органов и обеспечивает формирование нормальных стенок сосуда. Данный метод является успешным, но в краткосрочной перспективе, так как эти материалы стали причиной аномальных механических напряжений и нарушений артериального кровотока за счет возобновления роста стенок или образования тромбов [ | + | Для лечения заболеваний сердечно-сосудистой системы хирурги часто используют некоторые искусственные материалы, такие как стенты и протезы. Стент — специальная, изготовленная в форме цилиндрического каркаса упругая металлическая или пластиковая конструкция, которая помещается в просвет полых органов и обеспечивает формирование нормальных стенок сосуда. Данный метод является успешным, но в краткосрочной перспективе, так как эти материалы стали причиной аномальных механических напряжений и нарушений артериального кровотока за счет возобновления роста стенок или образования тромбов [3]. |
| − | Моделирование внутренней структуры стенок аорты представляет собой трудную задачу [ | + | Моделирование внутренней структуры стенок аорты представляет собой трудную задачу [2]. Однако, в ряде случаев оказываются вполне пригодными упрощенные модели, в частности, те, в которых используется модель тонкостенной эластичной трубки для стенки артерии [1, 4]. |
| − | Течение жидкости по тонкостенным эластичным трубкам можно условно разделить на три относительно самостоятельных гидродинамических явления: перенос объема жидкости по трубке, распространение волны давления (в биомеханике ее называют пульсовой волной), скорость которой обычно выше скорости жидкости, и возникновение высокочастотных колебаний вследствие потери устойчивости. Эти явления носят нелинейный характер и описываются уравнениями, следующими из уравнений Навье-Стокса [ | + | Течение жидкости по тонкостенным эластичным трубкам можно условно разделить на три относительно самостоятельных гидродинамических явления: перенос объема жидкости по трубке, распространение волны давления (в биомеханике ее называют пульсовой волной), скорость которой обычно выше скорости жидкости, и возникновение высокочастотных колебаний вследствие потери устойчивости. Эти явления носят нелинейный характер и описываются уравнениями, следующими из уравнений Навье-Стокса [1]. |
Одним из важных гемодинамических процессов является распространение пульсовой волны. Если регистрировать деформации стенки артерии в двух разноудаленных от сердца точках, то окажется, что деформация сосуда дойдет до более удаленной точки позже, то есть по сосуду распространяется волна пульсовых колебаний объема сосуда, давления и скорости кровотока, однозначно связанных друг c другом. Это так называемая пульсовая волна. Пульсовая волна - процесс распространения изменения объема вдоль эластичного сосуда в результате одновременного изменения в нем давления и массы жидкости. | Одним из важных гемодинамических процессов является распространение пульсовой волны. Если регистрировать деформации стенки артерии в двух разноудаленных от сердца точках, то окажется, что деформация сосуда дойдет до более удаленной точки позже, то есть по сосуду распространяется волна пульсовых колебаний объема сосуда, давления и скорости кровотока, однозначно связанных друг c другом. Это так называемая пульсовая волна. Пульсовая волна - процесс распространения изменения объема вдоль эластичного сосуда в результате одновременного изменения в нем давления и массы жидкости. | ||
| Строка 26: | Строка 26: | ||
*Для простоты рассматривается одномерная постановка задачи на основании ранее разработанной модели (Yomosa, 1987). | *Для простоты рассматривается одномерная постановка задачи на основании ранее разработанной модели (Yomosa, 1987). | ||
| − | == Постановка задачи: | + | == Постановка задачи: Уравнения == |
*Для жидкости внутри аорты справедливо уравнение движение в форме уравнения Эйлера: | *Для жидкости внутри аорты справедливо уравнение движение в форме уравнения Эйлера: | ||
[[Файл:Formula_1.jpg|150px|thumb|left]] | [[Файл:Formula_1.jpg|150px|thumb|left]] | ||
| − | ,где v(x,t) – скорости потока жидкости вдоль оси трубки, ρ – постоянная плотность жидкости, x – координата вдоль оси трубки, t – время, p(x,t) – давление жидкости. | + | ,где <math>v(x,t)</math> – скорости потока жидкости вдоль оси трубки,<math>ρ</math> – постоянная плотность жидкости, <math>x</math> – координата вдоль оси трубки,<math>t</math> – время, <math>p(x,t)</math> – давление жидкости. |
| Строка 36: | Строка 36: | ||
*Уравнение неразрывности с учетом переменного радиуса для площади поперечного сечения трубки: | *Уравнение неразрывности с учетом переменного радиуса для площади поперечного сечения трубки: | ||
[[Файл:Formula_2.jpg|200px|thumb|left]] | [[Файл:Formula_2.jpg|200px|thumb|left]] | ||
| − | ,где u(x,t) – радиальное упругое смещение стенки трубки, R=R(x) - радиус трубки. | + | ,где <math>u(x,t)</math> – радиальное упругое смещение стенки трубки, <math>R=R(x)</math> - радиус трубки. |
| Строка 45: | Строка 45: | ||
*Уравнение движения для сдвиговых волн для описания деформационных процессов в стенке для внешнего радиального напряжения: | *Уравнение движения для сдвиговых волн для описания деформационных процессов в стенке для внешнего радиального напряжения: | ||
[[Файл:Formula_3.jpg|250px|thumb|left]] | [[Файл:Formula_3.jpg|250px|thumb|left]] | ||
| − | ,где E - модуль Юнга, а параметр a характеризует нелинейную упругость, P - внешнее давление, P_0- атмосферное давление, ρ_0 - плотность материала стенки, константы h и H пропорциональны толщине стенки и учитывают ее тканевую структуру. | + | ,где <math>E</math> - модуль Юнга, а параметр <math>a</math> характеризует нелинейную упругость,<math>P</math> - внешнее давление, <math>P_0</math>- атмосферное давление,<math>ρ_0</math> - плотность материала стенки, константы <math>h</math> и <math>H</math> пропорциональны толщине стенки и учитывают ее тканевую структуру. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Постановка задачи: Модельное уравнение == | ||
| + | В известных работах рассматривались случаи постоянной величины радиуса <math>R</math> (Yomosa, 1987) и переменного радиуса <math>R</math>(Kraenkel et al., 2007). Мы будем рассматривать случай резких изменений, которому соответствует кусочно-непрерывный характер радиуса, при этом производные от радиуса в уравнениях учитываться не будут. | ||
| + | Новое модельное уравнение в виде модифицированного уравнения Буссинеска с пременными коэффициентами записывается в виде: | ||
| + | [[Файл:Formula_4.jpg|350px|thumb|left]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Точное решение в виде бегущей уединенной волны при постоянном значении радиуса R == | ||
| + | Точное решение модельного уравнения при постоянном значении радиуса <math>R</math> получено в виде(где <math>a_1</math> и <math>c_1</math>– комбинации коэффициентов модельного уравнения, характеризующие упругие свойства стенки <math>β</math> - свободный параметр.): | ||
| + | [[Файл:Formula_5.jpg|350px|thumb|left]] | ||
| + | [[Файл:Formula_6.jpg|250px|thumb|left|Амплитуда]] | ||
| + | [[Файл:Formula_7.jpg|250px|thumb|left|Скорость]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Численное исследование эволюции локализованной в волны в аорте == | ||
| + | В пакете Вольфрам Математика был разработан код, с помощью которого и были решены нелинейные уравнения в частных производных и произведена визуализация полученных решений. | ||
| + | Начальное условие: | ||
| + | [[Файл:Formula_8.jpg|350px|thumb|left]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Кусочно-непрерывный характер радиуса задается функцией(где <math>с_{11}</math> и <math>с_{21}</math>– размеры изменения глубины неоднородности,<math>x_{11}</math> и <math>x_{12}</math>– размеры изменения длины неоднородности,<math>k_m</math> и <math>k_n</math>– крутизна заднего и переднего фронта неоднородности соответственно): | ||
| + | [[Файл:Formula_9.jpg|450px|thumb|left]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Визуализация и анализ результатов == | ||
| + | |||
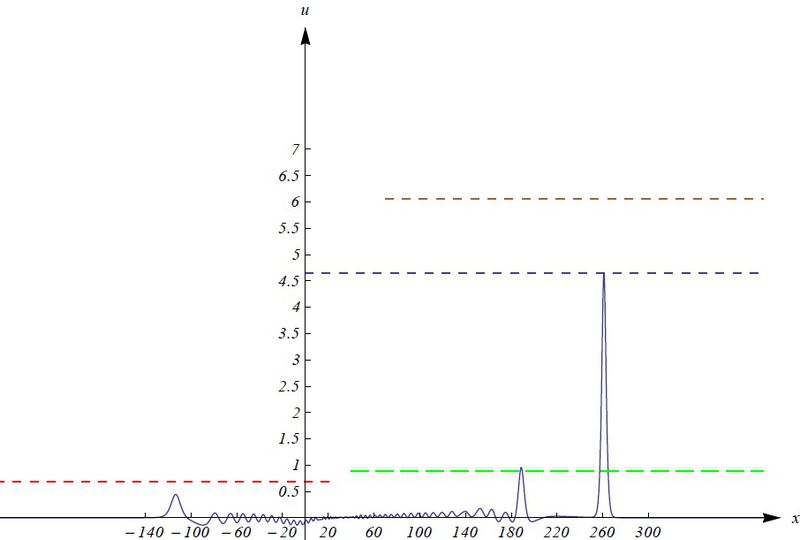
| + | [[Файл:150.jpg|800px|thumb|center|Поведение волны деформации при t=150, a = 0.5, β=0.4, c1=0.95]] | ||
| + | |||
| + | Синей пунктирной линией показано начальное значение амплитуды.Красной - максимальное значение амплитуды для образовавшейся отраженной волны. Зеленой пунктирной линией обозначено максимальное значение амплитуды вторичной волны. Коричневым цвет - максимальное значение амплитуды основной волны. | ||
| + | |||
| + | Исходя из визуализации данных делаем следующие выводы: | ||
| + | Амплитуда основной волны резко возрастает на подходе к неоднородности, достигает своего максимума внутри нее. После прохождения пораженного участка наблюдается снижение амплитуды до своего минимума, затем рост, до значения практически равного начальному значению амплитуды, с которой волна деформации продолжает распространяться до конца рассмотренного участка. Возрастание скорости наблюдается только при прохождении неоднородности. | ||
| + | Отраженная волна образуется внутри неоднородности и на рассмотренном участке распространяется с затухающей скоростью и амплитудой. | ||
| + | Вторичная волна образуется внутри неоднородности и распространяется с постоянной скоростью. Амплитуда распространения данной волны меняется на всем рассмотренном участке незначительно, на границах участка имеет одинаковые значения и является максимальной. | ||
| + | |||
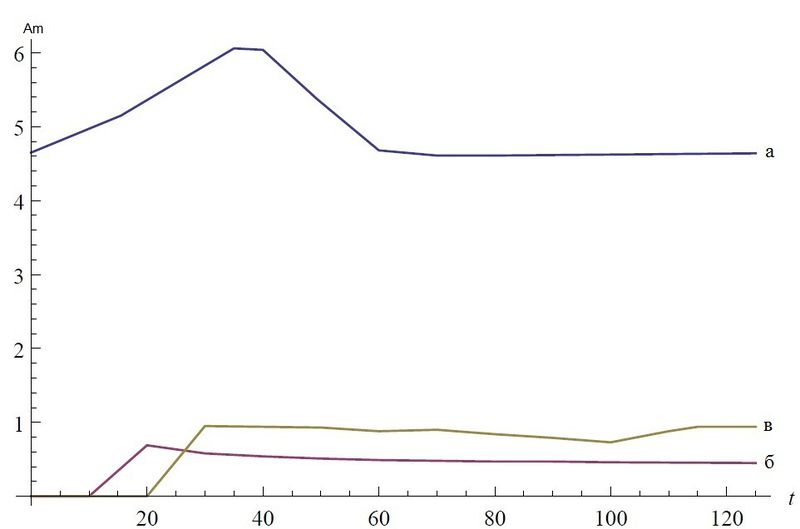
| + | На представленном ниже рисунке показано, как со временем меняется амплитуда трех волн деформации при рассмотренном случае моделирования неоднородности. | ||
| + | |||
| + | [[Файл:Am(t).jpg|800px|thumb|center|График зависимости амплитуды от времени при моделировании волны деформации в трубке с наличием неоднородности: | ||
| + | а – для основной волны, | ||
| + | б – для отраженной волны, | ||
| + | в – для вторичной волны. | ||
| + | ]] | ||
| + | |||
| + | == Задача акустодиагностики == | ||
| + | |||
| + | Задача акустодиагностики заключается в возможности сравнения скорости пульсовой волны, полученной на практике, со скоростью полученной на основе точного решения. После по изменению поведения проходящей вдоль аорты нелинейной волны деформации можно определить положение неоднородности и масштабы пораженного участка. | ||
| + | |||
| + | == Выводы == | ||
| + | *Получено модельное уравнение для поперечных волн деформации в виде модифицированного уравнения Буссинеска с переменными коэффициентами; | ||
| + | |||
| + | *Проведено численное исследование распространения локализованной волны деформации вдоль аорты, разработан код в среде Вольфрам Математика; | ||
| + | |||
| + | *Установлены основные качественные и количественные изменения в поведении волны при прохождении неоднородности: образование вторичной и отраженной локализованных волн; | ||
| + | |||
| + | *Установлено сходство этих волн с точным решением в виде бегущей уединенной волны; | ||
| + | |||
| + | *Это позволяет использовать выражения для параметров аналитического решения для определения параметров неоднородности по измеренным значениям амплитуды и скорости волны; | ||
| + | |||
| + | *Возможно дальнейшее использование модели для других частных случаев неоднородности, в частности, расширения стенок аорты; | ||
| + | |||
| + | *В перспективе применение модели на практике для диагностики характера и тяжести заболевания (акустодиагностики). | ||
| + | == Список литературы == | ||
| + | 1. А. Н. Волобуев. Течение жидкости в трубках с эластичными стенками // УФН. – 1995. - Т. 165. - №2. - С. 177 – 186. | ||
| + | |||
| + | 2. G. A. Holzapfel , T. C. Gasser, R. W. Ogden, A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models// Journal of Elasticity 61. 2000. 1–48. | ||
| + | |||
| + | 3. R. A. Kraenkel, S. Noubissie, P. Woafo. A mathematical model for wave propagation in elastic tubes with inhomogeneities: Application to blood waves propagation // Physica D 236. 2007. 131-140. | ||
| + | |||
| + | 4. S. Yomosa. Solitary Waves in Large Blood Vessels // J. Phys. Soc. Japan 56. 1987. 506-520. | ||
Текущая версия на 21:35, 14 июня 2015
Содержание
- 1 Руководитель
- 2 Введение
- 3 Цели
- 4 Постановка задачи: Модель
- 5 Постановка задачи: Уравнения
- 6 Постановка задачи: Модельное уравнение
- 7 Точное решение в виде бегущей уединенной волны при постоянном значении радиуса R
- 8 Численное исследование эволюции локализованной в волны в аорте
- 9 Визуализация и анализ результатов
- 10 Задача акустодиагностики
- 11 Выводы
- 12 Список литературы
Руководитель[править]
проф. дфмн. А.В. Порубов
Введение[править]
Аорта – самый крупный артериальный сосуд в теле человека, от которого отходят все артерии, образующие большой круг кровообращения.
С аортой связано множество заболеваний. Аневризма аорты – расширение участка аорты, обусловленное патологическим изменением соединительно-тканных структур ее стенок вследствие атеросклеротического процесса, воспалительного поражения, врожденной неполноценности или механических повреждений артериальной стенки.
Для лечения заболеваний сердечно-сосудистой системы хирурги часто используют некоторые искусственные материалы, такие как стенты и протезы. Стент — специальная, изготовленная в форме цилиндрического каркаса упругая металлическая или пластиковая конструкция, которая помещается в просвет полых органов и обеспечивает формирование нормальных стенок сосуда. Данный метод является успешным, но в краткосрочной перспективе, так как эти материалы стали причиной аномальных механических напряжений и нарушений артериального кровотока за счет возобновления роста стенок или образования тромбов [3].
Моделирование внутренней структуры стенок аорты представляет собой трудную задачу [2]. Однако, в ряде случаев оказываются вполне пригодными упрощенные модели, в частности, те, в которых используется модель тонкостенной эластичной трубки для стенки артерии [1, 4].
Течение жидкости по тонкостенным эластичным трубкам можно условно разделить на три относительно самостоятельных гидродинамических явления: перенос объема жидкости по трубке, распространение волны давления (в биомеханике ее называют пульсовой волной), скорость которой обычно выше скорости жидкости, и возникновение высокочастотных колебаний вследствие потери устойчивости. Эти явления носят нелинейный характер и описываются уравнениями, следующими из уравнений Навье-Стокса [1]. Одним из важных гемодинамических процессов является распространение пульсовой волны. Если регистрировать деформации стенки артерии в двух разноудаленных от сердца точках, то окажется, что деформация сосуда дойдет до более удаленной точки позже, то есть по сосуду распространяется волна пульсовых колебаний объема сосуда, давления и скорости кровотока, однозначно связанных друг c другом. Это так называемая пульсовая волна. Пульсовая волна - процесс распространения изменения объема вдоль эластичного сосуда в результате одновременного изменения в нем давления и массы жидкости.
В данной работе предлагается метод, с помощью которого наличие неоднородностей стенки аорты, образовавшихся в результате болезни или использования стента, можно обнаружить, наблюдая за изменением скорости и амплитуды волны деформации, распространяющейся вдоль стенки аорты.
Цели[править]
- Исследовать эволюцию нелинейных локализованных волн в аорте;
- Исследовать возможность использования этих волн для акустодиагностики неоднородностей на стенке аорты.
Постановка задачи: Модель[править]
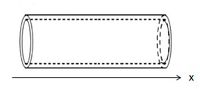
- Аорта - цилиндрическая упругая тонкостенная трубка;
- Кровь внутри аорты - идеальная несжимаемая жидкость;
- Для простоты рассматривается одномерная постановка задачи на основании ранее разработанной модели (Yomosa, 1987).
Постановка задачи: Уравнения[править]
- Для жидкости внутри аорты справедливо уравнение движение в форме уравнения Эйлера:
,где – скорости потока жидкости вдоль оси трубки, – постоянная плотность жидкости, – координата вдоль оси трубки, – время, – давление жидкости.
- Уравнение неразрывности с учетом переменного радиуса для площади поперечного сечения трубки:
,где – радиальное упругое смещение стенки трубки, - радиус трубки.
- Уравнение движения для сдвиговых волн для описания деформационных процессов в стенке для внешнего радиального напряжения:
,где - модуль Юнга, а параметр характеризует нелинейную упругость, - внешнее давление, - атмосферное давление, - плотность материала стенки, константы и пропорциональны толщине стенки и учитывают ее тканевую структуру.
Постановка задачи: Модельное уравнение[править]
В известных работах рассматривались случаи постоянной величины радиуса (Yomosa, 1987) и переменного радиуса (Kraenkel et al., 2007). Мы будем рассматривать случай резких изменений, которому соответствует кусочно-непрерывный характер радиуса, при этом производные от радиуса в уравнениях учитываться не будут. Новое модельное уравнение в виде модифицированного уравнения Буссинеска с пременными коэффициентами записывается в виде:
Точное решение в виде бегущей уединенной волны при постоянном значении радиуса R[править]
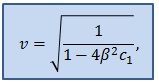
Точное решение модельного уравнения при постоянном значении радиуса получено в виде(где и – комбинации коэффициентов модельного уравнения, характеризующие упругие свойства стенки - свободный параметр.):
Численное исследование эволюции локализованной в волны в аорте[править]
В пакете Вольфрам Математика был разработан код, с помощью которого и были решены нелинейные уравнения в частных производных и произведена визуализация полученных решений. Начальное условие:
Кусочно-непрерывный характер радиуса задается функцией(где и – размеры изменения глубины неоднородности, и – размеры изменения длины неоднородности, и – крутизна заднего и переднего фронта неоднородности соответственно):
Визуализация и анализ результатов[править]
Синей пунктирной линией показано начальное значение амплитуды.Красной - максимальное значение амплитуды для образовавшейся отраженной волны. Зеленой пунктирной линией обозначено максимальное значение амплитуды вторичной волны. Коричневым цвет - максимальное значение амплитуды основной волны.
Исходя из визуализации данных делаем следующие выводы: Амплитуда основной волны резко возрастает на подходе к неоднородности, достигает своего максимума внутри нее. После прохождения пораженного участка наблюдается снижение амплитуды до своего минимума, затем рост, до значения практически равного начальному значению амплитуды, с которой волна деформации продолжает распространяться до конца рассмотренного участка. Возрастание скорости наблюдается только при прохождении неоднородности. Отраженная волна образуется внутри неоднородности и на рассмотренном участке распространяется с затухающей скоростью и амплитудой. Вторичная волна образуется внутри неоднородности и распространяется с постоянной скоростью. Амплитуда распространения данной волны меняется на всем рассмотренном участке незначительно, на границах участка имеет одинаковые значения и является максимальной.
На представленном ниже рисунке показано, как со временем меняется амплитуда трех волн деформации при рассмотренном случае моделирования неоднородности.
Задача акустодиагностики[править]
Задача акустодиагностики заключается в возможности сравнения скорости пульсовой волны, полученной на практике, со скоростью полученной на основе точного решения. После по изменению поведения проходящей вдоль аорты нелинейной волны деформации можно определить положение неоднородности и масштабы пораженного участка.
Выводы[править]
- Получено модельное уравнение для поперечных волн деформации в виде модифицированного уравнения Буссинеска с переменными коэффициентами;
- Проведено численное исследование распространения локализованной волны деформации вдоль аорты, разработан код в среде Вольфрам Математика;
- Установлены основные качественные и количественные изменения в поведении волны при прохождении неоднородности: образование вторичной и отраженной локализованных волн;
- Установлено сходство этих волн с точным решением в виде бегущей уединенной волны;
- Это позволяет использовать выражения для параметров аналитического решения для определения параметров неоднородности по измеренным значениям амплитуды и скорости волны;
- Возможно дальнейшее использование модели для других частных случаев неоднородности, в частности, расширения стенок аорты;
- В перспективе применение модели на практике для диагностики характера и тяжести заболевания (акустодиагностики).
Список литературы[править]
1. А. Н. Волобуев. Течение жидкости в трубках с эластичными стенками // УФН. – 1995. - Т. 165. - №2. - С. 177 – 186.
2. G. A. Holzapfel , T. C. Gasser, R. W. Ogden, A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models// Journal of Elasticity 61. 2000. 1–48.
3. R. A. Kraenkel, S. Noubissie, P. Woafo. A mathematical model for wave propagation in elastic tubes with inhomogeneities: Application to blood waves propagation // Physica D 236. 2007. 131-140.
4. S. Yomosa. Solitary Waves in Large Blood Vessels // J. Phys. Soc. Japan 56. 1987. 506-520.