Динамический гаситель — различия между версиями
| (не показано 9 промежуточных версий 3 участников) | |||
| Строка 3: | Строка 3: | ||
'''Динамический гаситель колебаний''' представляет собой колебательное звено, которое присоединяется к тому устройству, резонансное колебание которого необходимо подавить. Динамические гасители колебаний применяют, в основном, для виброзащиты специальных сооружений: башенных конструкций, мачт с оттяжками, опор линий электропередач, висячих мостов и переходов, металлических каркасных зданий и сооружений горнорудной промышленности. При этом снижение уровня колебаний сопровождается уменьшением динамических напряжений и увеличением долговечности гибких стальных сооружений. | '''Динамический гаситель колебаний''' представляет собой колебательное звено, которое присоединяется к тому устройству, резонансное колебание которого необходимо подавить. Динамические гасители колебаний применяют, в основном, для виброзащиты специальных сооружений: башенных конструкций, мачт с оттяжками, опор линий электропередач, висячих мостов и переходов, металлических каркасных зданий и сооружений горнорудной промышленности. При этом снижение уровня колебаний сопровождается уменьшением динамических напряжений и увеличением долговечности гибких стальных сооружений. | ||
| − | ''' | + | '''Постановка задачи'''<br /> |
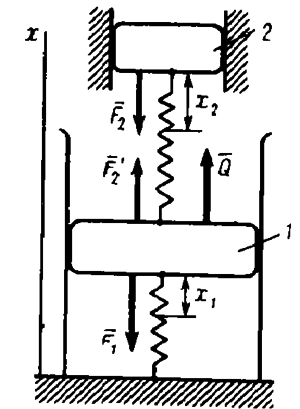
| − | + | Укрепленный на пружине груз ''1'' совершает вынужденные колебания под действием возмущающей силы <math> Q_{1} = Q_{0}sin(pt) </math>. Требуется погасить эти колебания, прикрепив к грузу ''1'' на пружине с коэффициентом жесткости <math> c_{2} </math> груз ''2'' массой <math> m_{2} </math>. | |
| + | [[Файл: GasDin.png|300px|Модель динамического гасителя]] | ||
| − | + | '''Основные уравнения'''<br /> | |
| − | |||
::<math> | ::<math> | ||
\left\{ | \left\{ | ||
\begin{array}{ll} | \begin{array}{ll} | ||
| − | + | m_{1} \ddot{x_{1}} = c_{1}x_{1} + c_{2}(x_{2}-x_{1})+ Q_{0}sin(pt)\\ | |
| − | \displaystyle | + | \displaystyle m_{2} \ddot{x_{2}} = -c_{2}(x_{2}-x_{1})\\ |
\end{array} | \end{array} | ||
\right. | \right. | ||
</math> | </math> | ||
| − | <math> | + | <math> x_{1},x_{2}</math> - обобщенные координаты <br /> |
| − | <math> | + | <math> m_{1} </math> - масса груза ''1''<br /> |
| − | <math> | + | <math> m_{2} </math> - масса груза ''2'' (гасителя)<br /> |
| − | <math> Q_{1} = Q_{0}sin(pt) </math> - внешняя сила,p - частота внешней силы<br /> | + | <math> c_{1},c_{2} </math> - жесткость грузов ''1'' и ''2'' соответственно <br /> |
| − | Условие гашения колебаний | + | <math> Q_{1} = Q_{0}sin(pt) </math> - внешняя сила, ''p'' - частота внешней силы<br /> |
| − | <big><math> \sqrt{\frac{ | + | Условие гашения колебаний: <br /> |
| + | <big><math> p = \sqrt{\frac{c_{2}}{m_{2}}} </math> | ||
</big> | </big> | ||
| − | |||
| − | |||
{{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Tenitskaya/DinGas/dingas.html |width=1000 |height=640 |border=0 }} | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Tenitskaya/DinGas/dingas.html |width=1000 |height=640 |border=0 }} | ||
Текущая версия на 13:13, 2 июня 2015
Виртуальная лаборатория>Динамический гасительДинамический гаситель колебаний представляет собой колебательное звено, которое присоединяется к тому устройству, резонансное колебание которого необходимо подавить. Динамические гасители колебаний применяют, в основном, для виброзащиты специальных сооружений: башенных конструкций, мачт с оттяжками, опор линий электропередач, висячих мостов и переходов, металлических каркасных зданий и сооружений горнорудной промышленности. При этом снижение уровня колебаний сопровождается уменьшением динамических напряжений и увеличением долговечности гибких стальных сооружений.
Постановка задачи
Укрепленный на пружине груз 1 совершает вынужденные колебания под действием возмущающей силы . Требуется погасить эти колебания, прикрепив к грузу 1 на пружине с коэффициентом жесткости груз 2 массой .
Основные уравнения
- обобщенные координаты
- масса груза 1
- масса груза 2 (гасителя)
- жесткость грузов 1 и 2 соответственно
- внешняя сила, p - частота внешней силы
Условие гашения колебаний:
Скачать Dingas.zip.
Файл "particle_in_well_2.js"
1 function MainParticle(canvas) {
2 // Предварительные установки
3 var context = canvas.getContext("2d"); // на context происходит рисование
4
5 // Задание констант
6 const Pi = 3.1415926; // число "пи"
7 const m0 = 1; // масштаб массы
8 const T0 = 1; // масштаб времени (период колебаний исходной системы)
9 const a0 = 1; // масштаб расстояния (диаметр шара)
10
11 const g0 = a0 / T0 / T0; // масштаб ускорения (ускорение, при котором за T0 будет пройдено расстояние a0)
12 const k0 = 2 * Pi / T0; // масштаб частоты
13 const C0 = m0 * k0 * k0; // масштаб жесткости
14 var scale1 = 0.5;
15 var scale2 = 0.5;
16 var coil = 7;
17 var coil2 = 5;
18 var t = 0;
19 var qq = 0;
20 // *** Задание физических параметров ***
21 var xShift= 0;
22 const Ny = 15; // число шаров, помещающихся по вертикали в окно (задает размер шара относительно размера окна)
23 const Nx = 15; // число шаров, помещающихся по вертикали в окно (задает размер шара относительно размера окна)
24 const l1 = 11*a0; // длина первой пружины
25 const l2 = 2*a0; // длина второй пружины
26 var m1 = 5 * m0; // масса первого шара
27 var m2 = 10 * m0; // масса второго шара
28 const Cwall = 10 * C0; // жесткость стен
29 const r = 1 * a0; // радиус частицы в расчетных координатах
30 var c1 = 100; // "жесткость" пружинки 1
31 var c2 = 100; // "жесткость" пружинки 1
32 var vx0 = 0 * a0/T0; //начальная скорость
33 var E = 0; //энергия системы
34 var Vmax = 0; var Mmin = 0; var Vprov = 0;
35 var dby, dcy, bc, cc;
36
37
38 //*** Передача значений слайдерам и текстовым окнам***
39 Text_m1.value = m1;
40 Text_m2.value = m2;
41 Text_c1.value = c1;
42 Text_c2.value = c2;
43
44 Slider_m1.min = 0.1;
45 Slider_m1.max = 10;
46 Slider_m1.step = 0.1;
47 Slider_m1.value = Text_m1.value;
48
49 Slider_m2.min = 0.1;
50 Slider_m2.max = 10;
51 Slider_m2.step = 0.1;
52 Slider_m2.value = Text_m2.value;
53
54 Slider_c2.min = 1; Slider_c1.min = 1;
55 Slider_c2.max = 200; Slider_c1.max = 200;
56 Slider_c2.step = 1; Slider_c1.step = 1;
57 Slider_c2.value = Text_c2.value; Slider_c1.value = Text_c1.value;
58
59 // *** Задание вычислительных параметров ***
60
61 const fps = 550; // frames per second - число кадров в секунду (качеcтво отображения)
62 const spf = 260; // steps per frame - число шагов интегрирования между кадрами (скорость расчета)
63 const dt = 0.01 * T0 / fps; // шаг интегрирования
64
65 // Задание констант для рисования
66 const scale = canvas.height / Ny * a0; // масштабный коэффициент для перехода от расчетных к экранным координатам
67
68 var w = canvas.width / scale; // ширина окна в расчетных координатах
69 var h = canvas.height / scale; // высота окна в расчетных координатах
70
71
72 // ------------------------------- Выполнение программы ------------------------------------------
73 // Добавление шара 1
74 var b = [];
75 var time = 1;
76 b.y = l1-h/2; b.x = h / 2; // расчетные координаты шара
77 b.y_ = b.y; b.x_ = b.x;
78 b.fy = 0; b.vy = 0; // начальная скорость
79 // Добавление шара 2
80 var c = [];
81 c.y = l2 + l1 - h/2; c.x = h / 2; // расчетные координаты шара
82 c.y_ = c.y; c.x_ = c.x;
83 c.fy = 0; c.vy = 0; // начальная скорость
84
85
86 // центр рамки
87 var origin = [];
88 origin.x = w/2; origin.y = h/2;
89 // стенка
90 var wall1 = [];
91 wall1.x = w/2 ; wall1.y = h/2;
92
93 // Основной цикл программы
94 setInterval(control, 1500 / fps); // функция control вызывается с периодом, определяемым вторым параметром
95
96 // ---------------------------------------------------------------------------------------------------------------------
97 // --------------------------------- Определение всех функций -----------------------------------
98 // ---------------------------------------------------------------------------------------------------------------------
99
100 // функция запускается при нажатии клавиши мыши
101 canvas.onmousedown = function(e)
102 {
103 var m = mouseCoords(e); // получаем координаты курсора мыши
104 context.clearRect(0, 0, w * scale, h* scale);
105 context.closePath();
106 context.fill();
107 var x = b.x*scale - m.x; // расстояние от центра шара до курсора по оси x
108 var y = b.y*scale - m.y; // расстояние от центра шара до курсора по оси y
109 var rLen2 = x * x + y * y; // квадрат расстояния между курсором и центром шара
110 //console.log(rLen2);
111 //console.log(100*r*r);
112 if (rLen2 <= 500 * r * r) // если курсор нажал на шар
113 {
114 yShift = b.y * scale - m.y; // сдвиг курсора относительно центра шара по x
115 canvas.onmousemove = mouseMove; // пока клавиша нажата - работает функция перемещения
116
117 }
118 }
119
120 // функция запускается при отпускании клавиши мыши
121 document.onmouseup = function()
122 {
123 canvas.onmousemove = null; // когда клавиша отпущена - функции перемещения нет
124 }
125
126 // функция запускается при перемещении мыши (много раз, в каждый момент перемещения)
127 // в нашем случае работает только с зажатой клавишей мыши
128 function mouseMove(e) {
129 context.clearRect(0, 0, w * scale, h* scale);
130 var m = mouseCoords(e); // получаем координаты курсора мыши
131 b.y = (m.y + yShift)/scale;
132 b.vy = 0; c.vy = 0;
133 //var scale1 = 0.0000000002;
134 //var scale2 = 0.2;
135
136 }
137
138 // функция возвращает координаты курсора мыши
139 function mouseCoords(e) {
140 var m = [] ;
141 var rect = canvas.getBoundingClientRect();
142 m.x = e.clientX - rect.left;
143 m.y = e.clientY - rect.top;
144 return m;
145 }
146 // основная функция, вызываемая в программе
147 function control()
148 {
149 physics(); // делаем spf шагов интегрирование
150 draw();
151
152 }
153
154 this.set_m1 = function(input)
155 {
156 m1 = Number(input);
157 context.clearRect(0, 0, w * scale, h* scale);
158 }
159
160 this.set_c1 = function(input)
161 {
162 c1 = Number(input);
163 context.clearRect(0, 0, w * scale, h* scale);
164 }
165
166 this.set_m2 = function(input)
167 {
168 m2 = Number(input);
169 context.clearRect(0, 0, w * scale, h* scale);
170 }
171
172 this.set_c2 = function(input)
173 {;
174 c2 = Number(input);
175 context.clearRect(0, 0, w * scale, h* scale);
176 }
177
178
179 // Функция, делающая spf шагов интегрирования
180 function physics()
181 {
182 b.y_ = b.y; b.vy_= b.vy; //записываем старые координаты и скорости
183 c.y_ = c.y; c.vy_= c.vy;
184 E_ = E;
185
186 for (var s = 1; s <= spf; s++)
187 {
188 b.vy += (c2*(-b.y + c.y - l2) - c1*(b.y - l1 + h/2))/m1*dt; //расчет скорости первого шара
189 c.vy += -c2*(c.y - b.y - l2)/m2*dt; //расчет скорости второго шара
190 if (c1/m1 == c2/m2) {
191 qq++;
192 b.vy = 0; c.vy = 0; t += dt;
193 wall1.y = h/2 + Math.sin(t);
194 if(qq == 1){
195 dby = b.y - l1 + h/2 ;
196 dcy = c.y -l2 - l1 + h/2;
197 bc = b.y;
198 cc = c.y;
199 }
200 if (qq<50001)
201 {
202 b.y = bc - dby/50000 + Math.sin(t); //расчет координаты первого шара
203 c.y = cc - dcy/50000 + Math.sin(t);
204 bc -= dby/50000;
205 cc -= dcy/50000;
206 wall1.y = h/2 + Math.sin(t);
207 }
208 else {
209 b.y = l1 - h/2 + Math.sin(t);
210 c.y = l2+l1-h/2+Math.sin(t);
211 }
212 }
213 if (c.vy != 0 && b.vy != 0)
214 {t += dt;
215 wall1.y = h/2 + Math.sin(t);
216 qq = 0;
217 }
218 b.y += b.vy*dt; //расчет координаты первого шара
219 c.y += c.vy*dt; //расчет координаты второго шара
220 E = 0.5*(m1*b.vy*b.vy + m2*c.vy*c.vy)+0.5*c2*(c.y - b.y -l2)*(c.y - b.y -l2)+0.5*c1*(b.y-l1)*(b.y - l1); //рачсет энергии системы
221 //Vprov = Math.max(b.vx, c.vx);
222 //if ((Vprov) > Vmax) Vmax = b.vx;
223
224 }
225
226 time = time + 1;
227
228 }
229
230 // определение функций, рисующих частицу, стенки и графики
231
232 function draw() //функция, рисующая шары, стенку и пружины
233 {
234 context.clearRect(0, 0, w * scale, h * scale); // очистить экран
235
236 // линия, соединяющая первую частицу со стенкой
237 context.beginPath();
238 for (var i = 0; i <= coil; i++ ) {
239 var x;
240 var y;
241 if (i != coil + 1) {
242 y = c.y*scale + ((b.y - c.y))*scale/coil*i;
243 x = canvas.width/2 + ((i%2==0)?-1:1)*8 + (b.x - a0)/coil*i;
244 } else {
245 y = c.y*scale + ((b.y - c.y))*scale/coil*(i+1);
246 x = canvas.width/2 + ((i%2==0)?1:-1)*8 + (b.x - a0)/coil*(i+1);
247 }
248 context.lineTo(x, y);
249 }
250 context.stroke();
251 // линия, соединяющая первую частицу со второй
252 context.beginPath();
253 for (var i = 0; i <= coil2; i++ ) {
254 var x;
255 var y;
256 if (i != coil2 + 1) {
257 y = wall1.y*scale + ((c.y - wall1.y))*scale/coil2*i;
258 x = canvas.width/2 + ((i%2==0)?-1:1)*8 + (b.x - a0)/coil*i;
259 } else {
260 y = wall1.y*scale + ((c.y - wall1.y))*scale/coil2*(i+1);
261 x = canvas.width/2 + ((i%2==0)?1:-1)*8 + (b.x - a0)/coil*(i+1);
262 }
263 context.lineTo(x, y);
264 }
265 context.stroke(); // стенка
266 context.moveTo((wall1.x+a0)*scale, wall1.y *scale );
267 context.lineTo((wall1.x-a0)*scale, wall1.y*scale );
268 context.closePath();
269 context.stroke();
270
271 // частица вторая
272 context.fillStyle = "#FF0A47";
273 context.beginPath();
274 context.arc(c.x * scale, c.y * scale, 0.5*r * scale, 0, 2*Math.PI, false);
275 context.fill();
276 //частица первая
277 context.fillStyle = "#0AC2FF";
278 context.beginPath();
279 context.arc(b.x * scale, b.y * scale, 0.5*r * scale, 0, 2*Math.PI, false);
280 context.fill();
281
282
283 }
284
285
286 }
Файл "dingas.html"
1 <!DOCTYPE html>
2 <html>
3 <head>
4 <title> Particle </title>
5 <script src="particle_in_well_2.js"></script>
6 </head>
7 <body>
8 <!-- Добавление области для рисования частицы -->
9 <canvas id="canvasBalls" width="500" height="500" style="border:1px solid #000000;"></canvas
10
11 <!-- Масса 1 -->
12 <div>
13 m1 =
14 <input id="Text_m1" style="width: 4.2ex;" required pattern="[-+]?([0-9]*\.[0-9]+|[0-9]+)" oninput="
15 if (!this.checkValidity()) return;
16 app.set_m1(this.value);
17 document.getElementById('Slider_m1').value = this.value;
18 ">
19 <input type = "range" id="Slider_m1" style="width: 100px;" oninput="app.set_m1(this.value); document.getElementById('Text_m1').value = this.value;">
20 </I></font>
21 </div>
22
23 <!-- Жесткость 1-->
24 <div>
25 c1 =
26 <input id="Text_c1" style="width: 4.2ex;" required pattern="[-+]?([0-9]*\.[0-9]+|[0-9]+)" oninput="
27 if (!this.checkValidity()) return;
28 app.set_c1(this.value);
29 document.getElementById('Slider_c1').value = this.value;
30 ">
31 <input type = "range" id="Slider_c1" style="width: 100px;" oninput="app.set_c1(this.value); document.getElementById('Text_c1').value = this.value;">
32 </I></font>
33 </div>
34
35 <!-- Масса 2-->
36 <div>
37 m2 =
38 <input id="Text_m2" style="width: 4.2ex;" required pattern="[-+]?([0-9]*\.[0-9]+|[0-9]+)" oninput="
39 if (!this.checkValidity()) return;
40 app.set_m2(this.value);
41 document.getElementById('Slider_m2').value = this.value;
42 ">
43 <input type = "range" id="Slider_m2" style="width: 100px;" oninput="app.set_m2(this.value); document.getElementById('Text_m2').value = this.value;">
44 </I></font>
45 </div>
46
47 <!--Жесткость 2 -->
48 <div>
49 c2 =
50 <input id="Text_c2" style="width: 4.2ex;" required pattern="[-+]?([0-9]*\.[0-9]+|[0-9]+)" oninput="
51 if (!this.checkValidity()) return;
52 app.set_c2(this.value);
53 document.getElementById('Slider_c2').value = this.value;
54
55
56 ">
57 <input type = "range" id="Slider_c2" style="width: 100px;" oninput="app.set_c2(this.value); document.getElementById('Text_c2').value = this.value;">
58
59 </I></font>
60 </div>
61 <script type="text/javascript"> app = new MainParticle(document.getElementById('canvasBalls'));</script>
62 </body>
63 </html>