Планетарный механизм — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
(→Решение) |
(→Решение) |
||
| (не показано 6 промежуточных версий этого же участника) | |||
| Строка 4: | Строка 4: | ||
== Решение == | == Решение == | ||
| − | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/filimonov/TMtrajectory.html |width= | + | {{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/filimonov/TMtrajectory.html |width=900 |height=450 |border=0 }} |
Программа: [[Медиа:TM.zip|скачать]] | Программа: [[Медиа:TM.zip|скачать]] | ||
| Строка 186: | Строка 186: | ||
</div> | </div> | ||
| − | == | + | == Используемые библиотеки == |
| + | |||
| + | * cloudflare.js | ||
| + | * dat.gui.js | ||
| + | * googleapis.js | ||
| + | * orbitControls.js | ||
| + | * stats.js | ||
| + | * trackballControls.js | ||
| + | |||
| + | ==Траектория движения точки== | ||
'''Эпицикло́ида''' — [[плоская кривая]], образуемая фиксированной точкой [[окружность|окружности]], катящейся по внешней стороне другой окружности без скольжения. | '''Эпицикло́ида''' — [[плоская кривая]], образуемая фиксированной точкой [[окружность|окружности]], катящейся по внешней стороне другой окружности без скольжения. | ||
Текущая версия на 12:51, 26 мая 2015
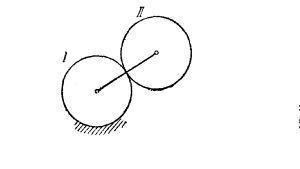
Задача: С помощью языка программирования JavaScript смоделировать планетарный механизм.
Решение[править]
Программа: скачать
Текст программы на языке JavaScript:
Файл "TMtrajectory.js"
1 function main()
2 {
3 var scene = new THREE.Scene();
4 var camera = new THREE.PerspectiveCamera(45, window.innerWidth/window.innerHeight, 0.1, 1000);
5 var render = new THREE.WebGLRenderer();
6 render.setClearColor(0xFFFFFF, 1);
7 render.setSize(window.innerWidth, window.innerHeight);
8
9
10 var geometry = new THREE.CylinderGeometry( 1, 1, 5, 32 );
11 var material = new THREE.MeshBasicMaterial( {color: 0x000000, wireframe:true} );
12 var cylinder1 = new THREE.Mesh( geometry, material );
13 scene.add( cylinder1 );
14 var geometry = new THREE.CylinderGeometry( 1, 1, 5, 32 );
15 var material = new THREE.MeshBasicMaterial( {color: 0x000000, wireframe:true} );
16 var cylinder = new THREE.Mesh( geometry, material );
17 scene.add( cylinder );
18 cylinder1.position.x=0;
19 cylinder1.position.y=2.5;
20 cylinder1.position.z=0;
21 cylinder.position.x=20;
22 cylinder.position.y=2.5;
23 cylinder.position.z=0;
24 scene.add(cylinder);
25
26
27 var geometry = new THREE.BoxGeometry( 20, 0.5, 0.5 );
28 var material = new THREE.MeshBasicMaterial( {color: 0x00ff00} );
29 var cube = new THREE.Mesh( geometry, material );
30 scene.add( cube );
31 cube.position.x=10;
32 cube.position.y=5;
33 cube.position.z=0;
34 /**cube.position.x=-4;
35 cube.position.y=3;
36 cube.position.z=0;
37 scene.add(cube);*/
38
39
40 var sphereGeometry = new THREE.SphereGeometry(0.5,20,20);
41 var sphereMaterial = new THREE.MeshLambertMaterial({color:0x7777ff, wireframe:false});
42 var ball = new THREE.Mesh(sphereGeometry, sphereMaterial)
43
44 scene.add(ball);
45
46 var sphereGeometry = new THREE.SphereGeometry(0.5,20,20);
47 var sphereMaterial = new THREE.MeshLambertMaterial({color:0x0000ff, wireframe:false});
48 var ball1 = new THREE.Mesh(sphereGeometry, sphereMaterial)
49
50 scene.add(ball1);
51
52
53 var spotLight = new THREE.SpotLight(0xffffff);
54 spotLight.position.set(10,30,30)
55 scene.add(spotLight);
56
57 var spotLight1 = new THREE.SpotLight(0xffffff);
58 spotLight.position.set(10,10,0)
59 scene.add(spotLight1);
60
61 render.shadowMapEnabled = true;
62 spotLight.castShadow = true;
63 spotLight1.castShadow = true;
64
65
66
67
68 camera.position.x= 0;
69 camera.position.y= 80;
70 camera.position.z= 0;
71 camera.lookAt(scene.position);
72 $("#webGL").append(render.domElement);
73
74
75
76 var controls = new function() {
77 this.rotationSpeed = 0.01;
78 this.Radius = 5;
79 }
80 var gui = new dat.GUI();
81 gui.add(controls, 'rotationSpeed',0,0.5);
82 gui.add(controls,'Radius',1,15);
83
84
85
86 control1 = new THREE.OrbitControls(camera);
87 control1.dumping = 0.2;
88
89
90 /**window.addEventListener('resize',onWindowResize,false);
91 function onWindowResize()
92 {
93 camera.aspect = window.innerWidth/window.innerHeight;
94 camera.updateProjectionMatrix();
95 render.setSize(window.innerWidth,window.innerHeight);
96
97 renderer();
98 }*/
99
100 var trajectoryGeometry = new THREE.SphereGeometry(0.05, 16, 16);
101 var trajectoryMaterial = new THREE.MeshBasicMaterial( {color: 0x000000,wireframe:true} );
102
103 var trajectoryGeometry1 = new THREE.SphereGeometry(0.05, 16, 16);
104 var trajectoryMaterial1 = new THREE.MeshBasicMaterial( {color: 0x0000ff,wireframe:true} );
105
106 var stats = initStats();
107 var step = 0;
108
109
110
111 renderer();
112 function renderer()
113 {
114 stats.update();
115
116 var r=20-controls.Radius;
117 var k = r/controls.Radius;
118
119 var r1=(20-controls.Radius)+controls.Radius/4;
120 var k1 = (r1)/(controls.Radius*0.5);
121
122 cylinder.position.x=20*(Math.cos(step));
123 cylinder.position.z=20*(Math.sin(step));
124 step+=controls.rotationSpeed*0.3;
125
126
127
128 cylinder.rotation.y-=controls.rotationSpeed;
129 cube.position.x=10*(Math.cos(step));
130 cube.position.z=10*(Math.sin(step));
131 cube.rotation.y-=controls.rotationSpeed*0.3;
132 requestAnimationFrame(renderer);
133 control1.update();
134 cylinder.scale.set(controls.Radius,1,controls.Radius);
135 cylinder1.scale.set(20-controls.Radius,1,20-controls.Radius);
136 render.render(scene,camera);
137 ball.position.x = controls.Radius*(k+1)*(Math.cos(step)-(Math.cos((k+1)*step))/(k+1));
138 ball.position.z = controls.Radius*(k+1)*(Math.sin(step)-(Math.sin((k+1)*step))/(k+1));
139 ball.position.y = 5;
140
141 ball1.position.x = 0.5*controls.Radius*(k1+1)*(Math.cos(step)-(Math.cos((k1+1)*step))/(k1+1));
142 ball1.position.z = 0.5*controls.Radius*(k1+1)*(Math.sin(step)-(Math.sin((k1+1)*step))/(k1+1));
143 ball1.position.y = 5;
144
145 var trajectory = new THREE.Mesh(trajectoryGeometry, trajectoryMaterial);
146 trajectory.position.x = ball.position.x;
147 trajectory.position.y = 5;
148 trajectory.position.z = ball.position.z;
149
150 var trajectory1 = new THREE.Mesh(trajectoryGeometry1, trajectoryMaterial1);
151 trajectory1.position.x = ball1.position.x;
152 trajectory1.position.y = 5;
153 trajectory1.position.z = ball1.position.z;
154
155 scene.add( trajectory );
156 scene.add( trajectory1 );
157
158 }
159
160 this.start = renderer;
161 }
162 function initStats()
163 {
164 var stats = new Stats();
165 stats.setMode(0);
166 stats.domElement.style.position='absolute';
167 stats.domElement.style.left = '0px';
168 stats.domElement.style.top = '0px';
169 $("#Stats").append(stats.domElement);
170 return stats;
171 }
Используемые библиотеки[править]
- cloudflare.js
- dat.gui.js
- googleapis.js
- orbitControls.js
- stats.js
- trackballControls.js
Траектория движения точки[править]
Эпицикло́ида — плоская кривая, образуемая фиксированной точкой окружности, катящейся по внешней стороне другой окружности без скольжения.
Уравнения[править]
Если центр неподвижной окружности находится в начале координат, её радиус равен , радиус катящейся по ней окружности равен , то эпициклоида описывается параметрическими уравнениями относительно :
где — угол поворота точки, описывающей эпициклоиду, относительно центра неподвижной окружности, — параметр, но фактически это угол наклона отрезка между центрами к оси .
Можно ввести величину , тогда уравнения предстанут в виде