КП: Динамика бильярда — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎См. также)
(→‎Обсуждение результатов и выводы)
 
(не показано 65 промежуточных версий 7 участников)
Строка 2: Строка 2:
  
  
−
'''''Курсовой проект по [[Теоретическая механика: физико-механический факультет|Теоретической механике]]'''''
+
'''''Курсовой проект по [[Теоретическая механика: физико-механический факультет|Теоретической механике]]''''' [[Файл:A1l3b.gif|thumb|Центральное разбиение |250px]]
  
−
'''Исполнитель:''' [[Булдаков Павел]]
+
'''Исполнитель:''' [[Булдаков Павел]]
  
 
'''Группа:''' [[Группа 09|09]] (23604)
 
'''Группа:''' [[Группа 09|09]] (23604)
Строка 11: Строка 11:
  
 
== Аннотация проекта ==
 
== Аннотация проекта ==
 +
Данный проект посвящен изучению динамики [https://ru.wikipedia.org/wiki/Бильярд бильярда] .В ходе работы над проектом было рассмотрено разбиение пирамиды из шаров, данный процесс смоделирован на языке [https://ru.wikipedia.org/wiki/JavaScript JavaScript].
 +
 +
== Формулировка задачи ==
 +
- Написать программу, моделирующую динамику взаимодействия шаров при игре в [https://ru.wikipedia.org/wiki/Бильярд Бильярд].  Взаимодействие между шарами описывается с помощью  [[Потенциал_Леннард-Джонса|потенциала Леннарда-Джонса]].
 +
<br />
 +
-Рассмотреть классическое разбиение в русском бильярде, проследить траекторию разлета.
 +
 +
== Общие сведения по теме ==
 +
Впервые о математическом базисе бильярдной игры заговорил [https://ru.wikipedia.org/wiki/Кориолис,_Гаспар-Гюстав Гаспар Гюстав Кориолис] в своей книге «Théorie mathématique du jeu de billard» (Русск. перевод: «Математическая теория явлений бильярдной игры») в 1835 году. Он использовал в своей работе элементы теории вероятностей, теории пределов и общего анализа. Однако особого интереса у современников книга не вызвала: ни у математиков, ни у бильярдистов.
 +
 +
Прошло более полутораста лет, и математический бильярд развился в свою теорию, породив несколько побочных. «Теория бильярдов» сегодня неотъемлемая часть [https://ru.wikipedia.org/wiki/Эргодичность эргодической] теории и теории динамических систем, имеет важнейшее применение в физике. Математиком Гальпериным создан способ [http://masseclub.ru/statji-o-biljjarde/poleznoe-o-biljjarde/matematicheskaja-teorija-biljjarda.html определения числа pi с помощью бильярда]. Намного ближе общеобразованному читателю результаты исследований математиков [http://masseclub.ru/statji-o-biljjarde/poleznoe-o-biljjarde/matematicheskaja-teorija-biljjarda.html Штайнхауса, Альхазена и Гарднера].
 +
 +
При реализации данной задачи используется стол с размерами игрового поля 2240 х 1120 мм, диаметром шара 68 мм и размерами луз 72 и 82 мм соответственно.
 +
 +
== Решение ==
 +
Приняты некоторые допущения:
 +
* все шары считаются идеально упругими и почти идеально жёсткими;
 +
* каждый шар имеет массу в 1 единицу и радиус в 1 единицу;
 +
* взаимодействие между двумя шарами описывается формулой
 +
<math>
 +
\left\{
 +
\begin{array}{ll}
 +
F_{LJ} = \frac{12D}{a}\left[\left(\frac a r\right)^{13}-\left(\frac a r\right)^{7}\right], \qquad & r<d; \\
 +
F_{LJ} = 0, \qquad & r > d; \\
 +
\end{array}
 +
\right.
 +
</math>
 +
 +
где d — расстояние между центрами шаров,<math>F_{LJ}(r)</math> — сила [[Потенциал Леннард-Джонса|Леннард-Джонса]]
 +
 +
 +
[http://mathoverflow.net/questions/156263/perfectly-centered-break-of-a-perfectly-aligned-pool-ball-rack/156407#156407 Профессор Джим Белк (Jim Belk)] рассчитал направление и скорость движения каждого из 15 шаров пирамиды, а также битка , после соударения.Для сравнения, помните, что начальная скорость битка была 10 ед/сек.
 +
<br>[[Файл:WHVJA1.png| Траектория разлета шаров при центральном разбиении пирамиды. |250px]] [[http://mathoverflow.net/questions/156263/perfectly-centered-break-of-a-perfectly-aligned-pool-ball-rack/156407#156407]] <br>
 +
[[Файл:017cae37a4318f94cff572023a52bddb.png|слева]]
 +
 +
 +
 +
 +
 +
 +
Ниже приведена программа( созданная совместно со [[Степанов Матвей|Степановым Матвеем]] на основании программы [[Динамика взаимодействующих частиц]]) , в которой видно, что траектория разлета шаров схожи с расчетными траекториями  профессора.
 +
 +
 +
{{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Stepanov/Billyard1version.html | справа |width=500|height=780 |border=0 }}
 +
 +
<div class="mw-collapsible mw-collapsed">
 +
'''Текст программы на языке JavaScript:''' <div class="mw-collapsible-content">
 +
Файл '''"Billyard1version.js"'''
 +
<syntaxhighlight lang="javascript" line start="1" enclose="div">
 +
 +
window.addEventListener("load", MainBalls, true);
 +
function MainBalls(slider_01, text_01, slider_02, text_02) {
 +
 +
    // Предварительные установки
 +
 +
    var canvas = canvasBalls;
 +
    var context = canvas.getContext("2d");                  // на context происходит рисование
 +
    canvas.oncontextmenu = function (e) {return false;};    // блокировка контекстного меню
 +
 +
    var Pi = 3.1415926;                  // число "пи"
 +
 +
    var m0 = 1;                          // масштаб массы
 +
    var T0 = 1;                          // масштаб времени (период колебаний исходной системы)
 +
    var a0 = 1;        // масштаб расстояния (диаметр шара)
 +
    var q = 90;                    // угол
 +
 
 +
 +
    var g0 = a0 / T0 / T0;                // масштаб ускорения (ускорение, при котором за T0 будет пройдено расстояние a0)
 +
    var k0 = 2 * Pi / T0;                // масштаб частоты
 +
    var C0 = m0 * k0 * k0;                // масштаб жесткости
 +
    var B0 = 2 * m0 * k0;                // масштаб вязкости
 +
  var v0 = 1;      //начальная скорость
 +
 +
 +
    // *** Задание физических параметров ***
 +
 +
    var Ny = 32;                          // число шаров, помещающихся по вертикали в окно (задает размер шара относительно размера окна)
 +
    var m = 1 * m0;                      // масса
 +
    var Cwall = 10 * C0;                  // жесткость стен
 +
    var Cball = 0.1 * Cwall;              // жесткость между частицами
 +
    var B = 0.008 * B0;                  // вязкость среды
 +
    var Bwall = 0.03 * B0;                // вязкость на стенках
 +
    var mg = 0.25 * m * g0;              // сила тяжести
 +
    var r = 0.5 * a0;                    // радиус частицы в расчетных координатах
 +
    var K = 0.85;                        // сила взаимодействия ограничивается значением, реализующимся при r/a = K
 +
    var a = 2 * r;                        // равновесное расстояние между частицами
 +
    var aCut = 2.00001 * r;              // радиус обрезания
 +
 +
    // *** Задание вычислительных параметров ***
 +
 +
    var fps = 50;                        // frames per second - число кадров в секунду (качечтво отображения)
 +
    var spf = 100;                        // steps per frame  - число шагов интегрирования между кадрами (скорость расчета)
 +
    var dt  = 0.045 * T0 / fps;          // шаг интегрирования (качество расчета)
 +
 +
    // Выполнение программы
 +
 +
    var scale = canvas.height / Ny / a0;  // масштабный коэффициент для перехода от расчетных к экранным координатам
 +
    var r2 = r * r;                      // ___в целях оптимизации___
 +
    var aCut2 = aCut * aCut;              // ___в целях оптимизации___
 +
    var a2 = a * a;                      // ___в целях оптимизации___
 +
    var D = a2 * Cball / 72;              // энергия связи между частицами
 +
    var LJCoeff = 12 * D / a2;            // коэффициент для расчета потенциала Л-Дж
 +
 
 +
    var Ka = K * a;                      // ___в целях оптимизации___
 +
    var K2a2 = K * K * a2;                // ___в целях оптимизации___
 +
 +
    var w = canvas.width / scale;          // ширина окна в расчетных координатах
 +
    var h = canvas.height / scale;          // высота окна в расчетных координатах
 +
 +
    // Работа с массивом
 +
 +
    var balls = [];                            // массив шаров
 +
    var addNewBall =  function(x, y) {
 +
        // проверка - не пересекается ли новый шар со стенами или уже существующими шарами
 +
        if (x - r < 0 || x + r > w || y - r < 0 || y + r > h) return null;
 +
        for (var i = 0; i < balls.length; i++) {
 +
            var rx = balls[i].x - x;
 +
            var ry = balls[i].y - y;
 +
            var rLen2 = rx * rx + ry * ry;
 +
            if (rLen2 < 4 * r2) return null;
 +
        }
 +
        var b = [];
 +
 +
        b.x = x;                b.y = y;        // расчетные координаты шара
 +
        b.fx = 0;              b.fy = 0;      // сила, действующая на шар
 +
        b.vx = 0;              b.vy = 0;      // скорость
 +
 +
        balls[balls.length] = b;                // добавить элемент в конец массива
 +
        return b;
 +
    };
 +
 +
    // Основной цикл программы
 +
 +
    function control() {
 +
        physics();
 +
        draw();
 +
    }
 +
 +
    // Расчетная часть программы
 +
 +
    function physics() {                        // то, что происходит каждый шаг времени
 +
        for (var s = 1; s <= spf; s++) {
 +
 +
            // пересчет сил идет отдельным массивом, т.к. далее будут добавляться силы взаимодействия между шарами
 +
            for (var i0 = 0; i0 < balls.length; i0++) {
 +
                balls[i0].fx = - B * balls[i0].vx;
 +
                balls[i0].fy = - B * balls[i0].vy;
 +
            }
 +
 +
            for (var i = 0; i < balls.length; i++) {  // пеерсчет взаимодействия между шарами
 +
 +
 +
    //попадание в лузу
 +
   
 +
      if ((balls[i].x >= (300/scale-r/2))  && (balls[i].y >= (300/scale-r/2)) && (balls[i].y <= (300/scale+r/2))) {balls.splice(i, 1)}; // когда координаты шара совпадают с координатами, записанными в условии цикла, шар удаляется с поля при помощи balls.splice
 +
    if ((balls[i].x >= (300/scale-r/2))  && (balls[i].y <= (r/2))) {balls.splice(i, 1)};
 +
    if ((balls[i].x >= (300/scale-r/2))  && (balls[i].y >= (600/scale -r/2))) {balls.splice(i, 1)};
 +
    if ((balls[i].x <= (r/2))  && (balls[i].y >= (600/scale -r/2))) {balls.splice(i, 1)};
 +
    if ((balls[i].x <= (r/2))  && (balls[i].y >= (300/scale-r/2)) && (balls[i].y <= (300/scale+r/2))) {balls.splice(i, 1)};
 +
    if ((balls[i].x <= (r/2))  && (balls[i].y <= (r/2))) {balls.splice(i, 1)}; 
 +
 +
                // расчет взаимодействия производится со всеми следующими шарами в массиве,
 +
                // чтобы не считать каждое взаимодействие дважды
 +
                var b = balls[i];
 +
                for (var j = i + 1; j < balls.length; j++) {
 +
                    var b2 = balls[j];
 +
                    var rx = b.x - b2.x;  var ry = b.y - b2.y;        // вектор смотрит на первый шар (b)
 +
                    var r2 = rx * rx + ry * ry;                        // квадрат расстояния между шарами
 +
                    if (r2 > aCut2) continue;                          // проверка на радиус обрезания
 +
                    var rLen = (Math.sqrt(r2));
 +
       
 +
 +
                    // если расстояние между частицами мало, силы будут посчитаны для K * a
 +
                    if (r2 < K2a2) {
 +
                        if (rLen > 0.00001) {                          // проверка, чтобы избежать деления на 0
 +
                            rx = rx / rLen * Ka;
 +
                            ry = ry / rLen * Ka;
 +
                        }
 +
                        r2 = K2a2;
 +
                        rLen = Ka;                                      // корень K2a2
 +
                    }
 +
 +
                    // сила взаимодействия
 +
                    var s2 = a2 / r2;        var s4 = s2 * s2;        // ___в целях оптимизации___
 +
                    var F = LJCoeff * s4 * s4 * (s4 * s2 - 1);          // сила взаимодействия Леннарда-Джонса
 +
 +
                    var Fx = F * rx;        var Fy = F * ry;
 +
                    b.fx += Fx;            b.fy += Fy;
 +
                    b2.fx -= Fx;            b2.fy -= Fy;
 +
                }
 +
 +
                if (b.y + r > h) { b.fy += -Cwall * (b.y + r - h) - Bwall * b.vy; }    // рассчет взаимодействия со стенками : когда координаты шара совпадают с координатами в условии цикла, шару придается скорость и направление
 +
                if (b.y - r < 0) { b.fy += -Cwall * (b.y - r) - Bwall * b.vy;}
 +
                if (b.x + r > w) { b.fx += -Cwall * (b.x + r - w) - Bwall * b.vx; }
 +
                if (b.x - r < 0) { b.fx += -Cwall * (b.x - r) - Bwall * b.vx; }
 +
 +
                b.vx += b.fx / m * dt;        b.vy += b.fy / m * dt;
 +
                b.x += b.vx * dt;            b.y += b.vy * dt;
 +
            }
 +
        }
 +
    }
 +
 +
    // Рисование
 +
 +
    var rScale13 = r * scale * 1.3;        // ___в целях оптимизации___
 +
    var rScaleShift = r * scale / 5;        // ___в целях оптимизации___
 +
  var line ;
 +
  var radi = 30;              // линия которая показывает предполагаему траекторию "битка"
 +
 
 +
    function draw() {
 +
        context.clearRect(0, 0, w * scale, h * scale);      // очистить экран
 +
        for (var i = 1; i < balls.length; i++){
 +
            var xS = balls[i].x * scale;          var yS = balls[i].y * scale;
 +
            // расчет градиента нужно проводить для каждого шара
 +
            var gradient = context.createRadialGradient(xS, yS, rScale13, xS - rScaleShift, yS + rScaleShift, 0);
 +
            gradient.addColorStop(0, "#fdebeb");
 +
            gradient.addColorStop(1, "#fffcfc");
 +
            context.fillStyle = gradient;
 +
 +
            context.beginPath();
 +
            context.arc(xS, yS, r * scale, 0, 2 * Math.PI, false);
 +
            context.closePath();
 +
            context.fill();
 +
        }
 +
    for (var i = 0; i < 1; i++){
 +
            var xS = balls[i].x * scale;          var yS = balls[i].y * scale;
 +
            // расчет градиента нужно проводить для каждого шара
 +
            var gradient = context.createRadialGradient(xS, yS, rScale13, xS - rScaleShift, yS + rScaleShift, 0);
 +
            gradient.addColorStop(0, "#cd0000");
 +
            gradient.addColorStop(1, "#fffcfc");
 +
            context.fillStyle = gradient;
 +
 +
            context.beginPath();
 +
            context.arc(xS, yS, r * scale, 0, 2 * Math.PI, false);
 +
            context.closePath();
 +
            context.fill();
 +
        }
 +
 +
   
 +
   
 +
      context.lineWidth="3";
 +
      context.strokeStyle="#fff506";
 +
            context.beginPath();
 +
            context.moveTo(balls[0].x * scale, balls[0].y * scale);                                                                                                                                                       
 +
      context.lineTo(radi*v0*Math.cos(q*Pi/180) + balls[0].x * scale,radi*v0*Math.sin(q*Pi/180)+balls[0].y * scale);
 +
            context.stroke();
 +
   
 +
 +
    // прорисовка луз
 +
    // verh lev
 +
  context.lineWidth="3";
 +
    context.strokeStyle="#ffffff ";
 +
    context.beginPath();
 +
    context.moveTo(0, 0);                                                                                                                                                       
 +
    context.lineTo(0,14 +2.5 );
 +
    context.stroke();
 +
 
 +
  context.lineWidth="3";
 +
    context.strokeStyle="#ffffff";
 +
    context.beginPath();
 +
    context.moveTo(0, 0);                                                                                                                                                       
 +
    context.lineTo(14 +2.5,0 );
 +
    context.stroke();
 +
 
 +
      // verh prav
 +
  context.lineWidth="3";
 +
    context.strokeStyle="#ffffff";
 +
    context.beginPath();
 +
    context.moveTo(286 - 2.5, 0);                                                                                                                                                       
 +
    context.lineTo(300,0 );
 +
    context.stroke();
 +
 
 +
  context.lineWidth="3";
 +
    context.strokeStyle="##ffffff";
 +
    context.beginPath();
 +
    context.moveTo(300, 0);                                                                                                                                                       
 +
    context.lineTo(300,14 +2.5 );
 +
    context.stroke();
 +
 
 +
        // niz lev
 +
  context.lineWidth="3";
 +
    context.strokeStyle="#ffffff";
 +
    context.beginPath();
 +
    context.moveTo(0, 600);                                                                                                                                                       
 +
    context.lineTo(14 +2.5,600 );
 +
    context.stroke();
 +
 
 +
  context.lineWidth="3";
 +
    context.strokeStyle="#ffffff";
 +
    context.beginPath();
 +
    context.moveTo(0, 586 - 2.5);                                                                                                                                                       
 +
    context.lineTo(0,600 );
 +
    context.stroke();
 +
   
 +
   
 +
    // niz prav
 +
  context.lineWidth="3";
 +
    context.strokeStyle="#ffffff";
 +
    context.beginPath();
 +
    context.moveTo(300, 600);                                                                                                                                                       
 +
    context.lineTo(300,586 - 2.5);
 +
    context.stroke();
 +
 
 +
  context.lineWidth="3";
 +
    context.strokeStyle="#ffffff";
 +
    context.beginPath();
 +
    context.moveTo(300, 600);                                                                                                                                                       
 +
    context.lineTo(286 - 2.5,600 );
 +
    context.stroke();
 +
 
 +
  //sered lev
 +
  context.lineWidth="3";
 +
    context.strokeStyle="#ffffff";
 +
    context.beginPath();
 +
    context.moveTo(0, 289);                                                                                                                                                       
 +
    context.lineTo(0,311);
 +
    context.stroke();
 +
 
 +
  //sered prav
 +
 
 +
  context.lineWidth="3";
 +
    context.strokeStyle="#ffffff";
 +
    context.beginPath();
 +
    context.moveTo(300, 289);                                                                                                                                                       
 +
    context.lineTo(300,311 );
 +
    context.stroke();
 +
   
 +
 
 +
    }
 +
 
 +
 +
    // Запуск системы
 +
                      // добавляем 20 частиц, сдвинув их от стен
 +
    addNewBall(16*w/32, 16*h/32 );
 +
    addNewBall(16*w/32, 8*h/32 ); 
 +
    addNewBall(16*w/32 - r,  8*h/32 - 1.7321*r); 
 +
    addNewBall(16*w/32 + r,  8*h/32 - 1.7321*r );
 +
    addNewBall(16*w/32,    8*h/32 - 2*1.7321*r );   
 +
    addNewBall(16*w/32 - 2*r,  8*h/32 - 2*1.7321*r );
 +
    addNewBall(16*w/32 + 2*r,  8*h/32 - 2*1.7321*r );
 +
    addNewBall(16*w/32 + r,  8*h/32 - 3*1.7321*r );
 +
    addNewBall(16*w/32 - r,  8*h/32 - 3*1.7321*r );
 +
    addNewBall(16*w/32 + 3*r,  8*h/32 - 3*1.7321*r );
 +
    addNewBall(16*w/32 - 3*r,  8*h/32 - 3*1.7321*r );
 +
    addNewBall(16*w/32,    8*h/32 - 4*1.7321*r );
 +
    addNewBall(16*w/32 - 2*r,  8*h/32 - 4*1.7321*r );
 +
    addNewBall(16*w/32 + 2*r,  8*h/32 - 4*1.7321*r );
 +
    addNewBall(16*w/32 - 4*r,  8*h/32 - 4*1.7321*r );
 +
    addNewBall(16*w/32 + 4*r,  8*h/32 - 4*1.7321*r );
 +
    addNewBall(16*w/32, 16*h/32 ); 
 +
   
 +
  this.setSlider_01 = function(c) { q=-c ;}; // функция для слайдера угла
 +
  this.setSlider_02 = function(c) { v0=c ;}; // функция для слайдера угла
 +
 +
// Настройка интерфейса
 +
 +
    slider_01.min = 0;              slider_01.max =360;
 +
    slider_01.step = 0.5;
 +
    slider_01.value = q;          // начальное значение ползунка должно задаваться после min и max
 +
    text_01.value = Math.abs(q);
 +
    slider_02.min = 0;              slider_02.max = 10;
 +
    slider_02.step = 0.5;
 +
    slider_02.value = v0;                // начальное значение ползунка должно задаваться после min и max
 +
    text_02.value = v0;
 +
 
 +
  this.setSlider_01(q);
 +
  this.setSlider_02(v0);
 +
   
 +
    this.newSystem = function() {
 +
    balls[0].vx = v0* Math.cos(q*Pi/180);
 +
        balls[0].vy = v0* Math.sin(q*Pi/180);
 +
  }
 +
 +
  this.newSystem1 = function() {
 +
  for (var i = 20; i >= 0; i--)
 +
  {balls.splice(i, 1)};
 +
  addNewBall(16*w/32, 16*h/32 );
 +
    addNewBall(16*w/32, 8*h/32 ); 
 +
    addNewBall(16*w/32 - r,  8*h/32 - 1.7321*r); 
 +
    addNewBall(16*w/32 + r,  8*h/32 - 1.7321*r );
 +
    addNewBall(16*w/32,    8*h/32 - 2*1.7321*r );   
 +
    addNewBall(16*w/32 - 2*r,  8*h/32 - 2*1.7321*r );
 +
    addNewBall(16*w/32 + 2*r,  8*h/32 - 2*1.7321*r );
 +
    addNewBall(16*w/32 + r,  8*h/32 - 3*1.7321*r );
 +
    addNewBall(16*w/32 - r,  8*h/32 - 3*1.7321*r );
 +
    addNewBall(16*w/32 + 3*r,  8*h/32 - 3*1.7321*r );
 +
    addNewBall(16*w/32 - 3*r,  8*h/32 - 3*1.7321*r );
 +
    addNewBall(16*w/32,    8*h/32 - 4*1.7321*r );
 +
    addNewBall(16*w/32 - 2*r,  8*h/32 - 4*1.7321*r );
 +
    addNewBall(16*w/32 + 2*r,  8*h/32 - 4*1.7321*r );
 +
    addNewBall(16*w/32 - 4*r,  8*h/32 - 4*1.7321*r );
 +
    addNewBall(16*w/32 + 4*r,  8*h/32 - 4*1.7321*r );
 +
    addNewBall(16*w/32, 16*h/32 ); 
 +
 
 +
}
 +
    setInterval(control, 1000 / fps);
 +
}
 +
 +
  
  
−
== Формулировка задачи ==
+
</syntaxhighlight>
 +
Файл '''"Billyard1version.html"'''
 +
<syntaxhighlight lang="javascript" line start="1" enclose="div">
 +
<!DOCTYPE html>
 +
<html>
 +
<head>
 +
    <title>Billyard</title>
 +
    <script src="Billyard1version.js"></script>
 +
</head>
 +
<body>
 +
    <canvas id="canvasBalls" width="300" height="600" style="border:1px none #000000;background: #008000"></canvas>
 +
<br>
 +
    <div>Угол:
 +
        <input type="range" id="slider_01" style="width: 150px;" oninput="app.setSlider_01(this.value); document.getElementById('text_01').value = this.value;">
 +
      q =
 +
        <input id="text_01" style="width: 5ex;" required pattern="[-+]?([0-9]*\.[0-9]+|[0-9]+)"  oninput="
 +
            // если введено не число - строка не пройдет валидацию по паттерну выше, и checkValidity() вернет false
 +
            if (!this.checkValidity()) return;
 +
            app.setSlider_01(this.value);
 +
            document.getElementById('slider_01').value = this.value;
 +
        ">
 +
    </div><br>
 +
 
 +
    <div>Начальная скорость:
 +
        <input type="range" id="slider_02" style="width: 150px;" oninput="app.setSlider_02(this.value); document.getElementById('text_02').value = this.value;">
 +
      v0 =
 +
        <input id="text_02" style="width: 5ex;" required pattern="[-+]?([0-9]*\.[0-9]+|[0-9]+)" oninput="
 +
            // если введено не число - строка не пройдет валидацию по паттерну выше, и checkValidity() вернет false
 +
            if (!this.checkValidity()) return;
 +
            app.setSlider_02(this.value);
 +
            document.getElementById('slider_02').value = this.value;
 +
        ">
 +
    </div><br>
 +
 
 +
 
 +
  <input type="button" style="width: 50px" name="" onclick="app.newSystem();return false;" value="PLAY"/>
 +
  <input type="button" style="width: 50px" name="" onclick="app.newSystem1();return false;" value="AGAIN"/>
 +
 
 +
<script type="text/javascript">var app = new MainBalls(
 +
            document.getElementById('slider_01'),
 +
            document.getElementById('text_01'),
 +
            document.getElementById('slider_02'),
 +
            document.getElementById('text_02')
 +
    );</script>
 +
</body>
 +
</html>
 +
</syntaxhighlight>
 +
</div>
 +
 
 +
 
 +
 
 +
В реальности данная картина так же видна, хоть и не столь явно из-за неидеальности системы .
 +
 
 +
 
 +
 
 +
 
 +
[[Файл:1.gif]]
  
  
−
== Общие сведения по теме ==
+
[[Файл:2.gif]]
  
  
−
== Решение ==
 
  
 +
[[Файл:3.gif]]
  
 
== Обсуждение результатов и выводы ==
 
== Обсуждение результатов и выводы ==
 +
В ходе работы над проектом была написана программа, моделирующая процесс игры в бильярд. Данная программа показывает, что траектория разлета шаров после центрального удара не зависит от силы удара, но зависит от малейшего изменения угла, так как меняется распространение ударной волны в пирамиде. При силе, достаточной для визуально заметного разлета шаров, при изменении угла на 1 градус - полное отклонение от симметрии, при 0.1 - заметное отклонение от симметрии, при 0.01 - трудно различимое.
  
  
 
<br>
 
<br>
−
Скачать отчет:
+
Скачать отчет:[[Медиа:Buldakov.docx|docx]]
 
<br>
 
<br>
−
Скачать презентацию:
 
  
 
== Ссылки по теме ==
 
== Ссылки по теме ==
−
 
+
* [http://publ.lib.ru/ARCHIVES/K/KORIOLIS_Gaspar_Gyustav/_Koriolis_G.G..html, Математическая теория явлений бильярдной игры - Г. Кориолис.]
−
 
+
*[[Потенциал_Леннард-Джонса|потенциала Леннарда-Джонса]]
 +
*[https://ru.wikipedia.org/wiki/JavaScript JavaScript]
 +
*[http://mathoverflow.net/questions/156263/perfectly-centered-break-of-a-perfectly-aligned-pool-ball-rack/156407#156407 Профессор Джим Белк (Jim Belk)]
 
== См. также ==
 
== См. также ==
  
 
* [[Справка:Содержание|Справочная информация]]
 
* [[Справка:Содержание|Справочная информация]]
−
* [[Курсовые проекты]]
+
* [[Курсовые проекты ТМ]]
  
  
 
[[Category: Студенческие проекты]]
 
[[Category: Студенческие проекты]]

Текущая версия на 05:06, 4 июня 2015

А.М. Кривцов > Теоретическая механика > Курсовые проекты ТМ 2015 > Динамика бильярда


Курсовой проект по Теоретической механике
Центральное разбиение

Исполнитель: Булдаков Павел

Группа: 09 (23604)

Семестр: весна 2015

Аннотация проекта[править]

Данный проект посвящен изучению динамики бильярда .В ходе работы над проектом было рассмотрено разбиение пирамиды из шаров, данный процесс смоделирован на языке JavaScript.

Формулировка задачи[править]

- Написать программу, моделирующую динамику взаимодействия шаров при игре в Бильярд. Взаимодействие между шарами описывается с помощью потенциала Леннарда-Джонса.
-Рассмотреть классическое разбиение в русском бильярде, проследить траекторию разлета.

Общие сведения по теме[править]

Впервые о математическом базисе бильярдной игры заговорил Гаспар Гюстав Кориолис в своей книге «Théorie mathématique du jeu de billard» (Русск. перевод: «Математическая теория явлений бильярдной игры») в 1835 году. Он использовал в своей работе элементы теории вероятностей, теории пределов и общего анализа. Однако особого интереса у современников книга не вызвала: ни у математиков, ни у бильярдистов.

Прошло более полутораста лет, и математический бильярд развился в свою теорию, породив несколько побочных. «Теория бильярдов» сегодня неотъемлемая часть эргодической теории и теории динамических систем, имеет важнейшее применение в физике. Математиком Гальпериным создан способ определения числа pi с помощью бильярда. Намного ближе общеобразованному читателю результаты исследований математиков Штайнхауса, Альхазена и Гарднера.

При реализации данной задачи используется стол с размерами игрового поля 2240 х 1120 мм, диаметром шара 68 мм и размерами луз 72 и 82 мм соответственно.

Решение[править]

Приняты некоторые допущения:

  • все шары считаются идеально упругими и почти идеально жёсткими;
  • каждый шар имеет массу в 1 единицу и радиус в 1 единицу;
  • взаимодействие между двумя шарами описывается формулой

[math] \left\{ \begin{array}{ll} F_{LJ} = \frac{12D}{a}\left[\left(\frac a r\right)^{13}-\left(\frac a r\right)^{7}\right], \qquad & r\lt d; \\ F_{LJ} = 0, \qquad & r \gt d; \\ \end{array} \right. [/math]

где d — расстояние между центрами шаров,[math]F_{LJ}(r)[/math] — сила Леннард-Джонса


Профессор Джим Белк (Jim Belk) рассчитал направление и скорость движения каждого из 15 шаров пирамиды, а также битка , после соударения.Для сравнения, помните, что начальная скорость битка была 10 ед/сек.
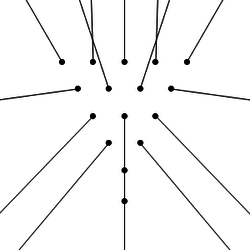Траектория разлета шаров при центральном разбиении пирамиды. [[1]]

017cae37a4318f94cff572023a52bddb.png




Ниже приведена программа( созданная совместно со Степановым Матвеем на основании программы Динамика взаимодействующих частиц) , в которой видно, что траектория разлета шаров схожи с расчетными траекториями профессора.


Текст программы на языке JavaScript:

Файл "Billyard1version.js" 

  1 window.addEventListener("load", MainBalls, true);
  2 function MainBalls(slider_01, text_01, slider_02, text_02) {
  3 
  4     // Предварительные установки
  5 
  6     var canvas = canvasBalls;
  7     var context = canvas.getContext("2d");                  // на context происходит рисование
  8     canvas.oncontextmenu = function (e) {return false;};    // блокировка контекстного меню
  9 
 10     var Pi = 3.1415926;                   // число "пи"
 11 
 12     var m0 = 1;                           // масштаб массы
 13     var T0 = 1;                           // масштаб времени (период колебаний исходной системы)
 14     var a0 = 1;        // масштаб расстояния (диаметр шара)
 15     var q = 90;                     // угол 
 16   
 17 
 18     var g0 = a0 / T0 / T0;                // масштаб ускорения (ускорение, при котором за T0 будет пройдено расстояние a0)
 19     var k0 = 2 * Pi / T0;                 // масштаб частоты
 20     var C0 = m0 * k0 * k0;                // масштаб жесткости
 21     var B0 = 2 * m0 * k0;                 // масштаб вязкости
 22   var v0 = 1;      //начальная скорость
 23 
 24 
 25     // *** Задание физических параметров ***
 26 
 27     var Ny = 32;                          // число шаров, помещающихся по вертикали в окно (задает размер шара относительно размера окна)
 28     var m = 1 * m0;                       // масса
 29     var Cwall = 10 * C0;                  // жесткость стен
 30     var Cball = 0.1 * Cwall;              // жесткость между частицами
 31     var B = 0.008 * B0;                   // вязкость среды
 32     var Bwall = 0.03 * B0;                // вязкость на стенках
 33     var mg = 0.25 * m * g0;               // сила тяжести
 34     var r = 0.5 * a0;                     // радиус частицы в расчетных координатах
 35     var K = 0.85;                         // сила взаимодействия ограничивается значением, реализующимся при r/a = K
 36     var a = 2 * r;                        // равновесное расстояние между частицами
 37     var aCut = 2.00001 * r;               // радиус обрезания
 38 
 39     // *** Задание вычислительных параметров ***
 40 
 41     var fps = 50;                         // frames per second - число кадров в секунду (качечтво отображения)
 42     var spf = 100;                        // steps per frame   - число шагов интегрирования между кадрами (скорость расчета)
 43     var dt  = 0.045 * T0 / fps;           // шаг интегрирования (качество расчета)
 44 
 45     // Выполнение программы
 46 
 47     var scale = canvas.height / Ny / a0;  // масштабный коэффициент для перехода от расчетных к экранным координатам
 48     var r2 = r * r;                       // ___в целях оптимизации___
 49     var aCut2 = aCut * aCut;              // ___в целях оптимизации___
 50     var a2 = a * a;                       // ___в целях оптимизации___
 51     var D = a2 * Cball / 72;              // энергия связи между частицами
 52     var LJCoeff = 12 * D / a2;            // коэффициент для расчета потенциала Л-Дж
 53   
 54     var Ka = K * a;                       // ___в целях оптимизации___
 55     var K2a2 = K * K * a2;                // ___в целях оптимизации___
 56 
 57     var w = canvas.width / scale;           // ширина окна в расчетных координатах
 58     var h = canvas.height / scale;          // высота окна в расчетных координатах
 59 
 60     // Работа с массивом
 61 
 62     var balls = [];                             // массив шаров
 63     var addNewBall =  function(x, y) {
 64         // проверка - не пересекается ли новый шар со стенами или уже существующими шарами
 65         if (x - r < 0 || x + r > w || y - r < 0 || y + r > h) return null;
 66         for (var i = 0; i < balls.length; i++) {
 67             var rx = balls[i].x - x;
 68             var ry = balls[i].y - y;
 69             var rLen2 = rx * rx + ry * ry;
 70             if (rLen2 < 4 * r2) return null;
 71         }
 72         var b = [];
 73 
 74         b.x = x;                b.y = y;        // расчетные координаты шара
 75         b.fx = 0;               b.fy = 0;      // сила, действующая на шар
 76         b.vx = 0;               b.vy = 0;       // скорость
 77 
 78         balls[balls.length] = b;                // добавить элемент в конец массива
 79         return b;
 80     };
 81 
 82     // Основной цикл программы
 83 
 84     function control() {
 85         physics();
 86         draw();
 87     }
 88 
 89     // Расчетная часть программы
 90 
 91     function physics() {                        // то, что происходит каждый шаг времени
 92         for (var s = 1; s <= spf; s++) {
 93 
 94             // пересчет сил идет отдельным массивом, т.к. далее будут добавляться силы взаимодействия между шарами
 95             for (var i0 = 0; i0 < balls.length; i0++) {
 96                 balls[i0].fx = - B * balls[i0].vx;
 97                 balls[i0].fy = - B * balls[i0].vy;
 98             }
 99 
100             for (var i = 0; i < balls.length; i++) {  // пеерсчет взаимодействия между шарами
101 
102 
103     //попадание в лузу 
104     
105       if ((balls[i].x >= (300/scale-r/2))  && (balls[i].y >= (300/scale-r/2)) && (balls[i].y <= (300/scale+r/2))) {balls.splice(i, 1)}; // когда координаты шара совпадают с координатами, записанными в условии цикла, шар удаляется с поля при помощи balls.splice
106     if ((balls[i].x >= (300/scale-r/2))   && (balls[i].y <= (r/2))) {balls.splice(i, 1)};
107     if ((balls[i].x >= (300/scale-r/2))   && (balls[i].y >= (600/scale -r/2))) {balls.splice(i, 1)};
108     if ((balls[i].x <= (r/2))   && (balls[i].y >= (600/scale -r/2))) {balls.splice(i, 1)};
109     if ((balls[i].x <= (r/2))  && (balls[i].y >= (300/scale-r/2)) && (balls[i].y <= (300/scale+r/2))) {balls.splice(i, 1)};
110     if ((balls[i].x <= (r/2))   && (balls[i].y <= (r/2))) {balls.splice(i, 1)};  
111 
112                 // расчет взаимодействия производится со всеми следующими шарами в массиве,
113                 // чтобы не считать каждое взаимодействие дважды
114                 var b = balls[i];
115                 for (var j = i + 1; j < balls.length; j++) {
116                     var b2 = balls[j];
117                     var rx = b.x - b2.x;   var ry = b.y - b2.y;         // вектор смотрит на первый шар (b)
118                     var r2 = rx * rx + ry * ry;                         // квадрат расстояния между шарами
119                     if (r2 > aCut2) continue;                           // проверка на радиус обрезания
120                     var rLen = (Math.sqrt(r2));
121         
122 
123                     // если расстояние между частицами мало, силы будут посчитаны для K * a
124                     if (r2 < K2a2) {
125                         if (rLen > 0.00001) {                           // проверка, чтобы избежать деления на 0
126                             rx = rx / rLen * Ka;
127                             ry = ry / rLen * Ka;
128                         }
129                         r2 = K2a2;
130                         rLen = Ka;                                      // корень K2a2
131                     }
132 
133                     // сила взаимодействия
134                     var s2 = a2 / r2;         var s4 = s2 * s2;         // ___в целях оптимизации___
135                     var F = LJCoeff * s4 * s4 * (s4 * s2 - 1);          // сила взаимодействия Леннарда-Джонса
136 
137                     var Fx = F * rx;        var Fy = F * ry;
138                     b.fx += Fx;             b.fy += Fy;
139                     b2.fx -= Fx;            b2.fy -= Fy;
140                 }
141 
142                 if (b.y + r > h) { b.fy += -Cwall * (b.y + r - h) - Bwall * b.vy; }    // рассчет взаимодействия со стенками : когда координаты шара совпадают с координатами в условии цикла, шару придается скорость и направление 
143                 if (b.y - r < 0) { b.fy += -Cwall * (b.y - r) - Bwall * b.vy;}
144                 if (b.x + r > w) { b.fx += -Cwall * (b.x + r - w) - Bwall * b.vx; }
145                 if (b.x - r < 0) { b.fx += -Cwall * (b.x - r) - Bwall * b.vx; }
146 
147                 b.vx += b.fx / m * dt;        b.vy += b.fy / m * dt;
148                 b.x += b.vx * dt;             b.y += b.vy * dt;
149             }
150         }
151     }
152 
153     // Рисование
154 
155     var rScale13 = r * scale * 1.3;         // ___в целях оптимизации___
156     var rScaleShift = r * scale / 5;        // ___в целях оптимизации___
157   var line ;
158   var radi = 30;              // линия которая показывает предполагаему траекторию "битка"
159   
160     function draw() {
161         context.clearRect(0, 0, w * scale, h * scale);      // очистить экран
162         for (var i = 1; i < balls.length; i++){
163             var xS = balls[i].x * scale;           var yS = balls[i].y * scale;
164             // расчет градиента нужно проводить для каждого шара
165             var gradient = context.createRadialGradient(xS, yS, rScale13, xS - rScaleShift, yS + rScaleShift, 0);
166             gradient.addColorStop(0, "#fdebeb");
167             gradient.addColorStop(1, "#fffcfc");
168             context.fillStyle = gradient;
169 
170             context.beginPath();
171             context.arc(xS, yS, r * scale, 0, 2 * Math.PI, false);
172             context.closePath();
173             context.fill();
174         }
175     for (var i = 0; i < 1; i++){
176             var xS = balls[i].x * scale;           var yS = balls[i].y * scale;
177             // расчет градиента нужно проводить для каждого шара
178             var gradient = context.createRadialGradient(xS, yS, rScale13, xS - rScaleShift, yS + rScaleShift, 0);
179             gradient.addColorStop(0, "#cd0000");
180             gradient.addColorStop(1, "#fffcfc");
181             context.fillStyle = gradient;
182 
183             context.beginPath();
184             context.arc(xS, yS, r * scale, 0, 2 * Math.PI, false);
185             context.closePath();
186             context.fill();
187         }
188 
189     
190     
191       context.lineWidth="3";
192       context.strokeStyle="#fff506";
193             context.beginPath();
194             context.moveTo(balls[0].x * scale, balls[0].y * scale);                                                                                                                                                         
195       context.lineTo(radi*v0*Math.cos(q*Pi/180) + balls[0].x * scale,radi*v0*Math.sin(q*Pi/180)+balls[0].y * scale);
196             context.stroke();
197     
198 
199     // прорисовка луз
200     // verh lev
201   context.lineWidth="3";
202     context.strokeStyle="#ffffff ";
203     context.beginPath();
204     context.moveTo(0, 0);                                                                                                                                                         
205     context.lineTo(0,14 +2.5 );
206     context.stroke();
207   
208   context.lineWidth="3";
209     context.strokeStyle="#ffffff";
210     context.beginPath();
211     context.moveTo(0, 0);                                                                                                                                                         
212     context.lineTo(14 +2.5,0 );
213     context.stroke();
214   
215       // verh prav
216   context.lineWidth="3";
217     context.strokeStyle="#ffffff";
218     context.beginPath();
219     context.moveTo(286 - 2.5, 0);                                                                                                                                                         
220     context.lineTo(300,0 );
221     context.stroke();
222   
223   context.lineWidth="3";
224     context.strokeStyle="##ffffff";
225     context.beginPath();
226     context.moveTo(300, 0);                                                                                                                                                         
227     context.lineTo(300,14 +2.5 );
228     context.stroke();
229   
230         // niz lev
231   context.lineWidth="3";
232     context.strokeStyle="#ffffff";
233     context.beginPath();
234     context.moveTo(0, 600);                                                                                                                                                         
235     context.lineTo(14 +2.5,600 );
236     context.stroke();
237   
238   context.lineWidth="3";
239     context.strokeStyle="#ffffff";
240     context.beginPath();
241     context.moveTo(0, 586 - 2.5);                                                                                                                                                         
242     context.lineTo(0,600 );
243     context.stroke();
244     
245     
246     // niz prav
247   context.lineWidth="3";
248     context.strokeStyle="#ffffff";
249     context.beginPath();
250     context.moveTo(300, 600);                                                                                                                                                         
251     context.lineTo(300,586 - 2.5);
252     context.stroke();
253   
254   context.lineWidth="3";
255     context.strokeStyle="#ffffff";
256     context.beginPath();
257     context.moveTo(300, 600);                                                                                                                                                         
258     context.lineTo(286 - 2.5,600 );
259     context.stroke();
260   
261   //sered lev
262   context.lineWidth="3";
263     context.strokeStyle="#ffffff";
264     context.beginPath();
265     context.moveTo(0, 289);                                                                                                                                                         
266     context.lineTo(0,311);
267     context.stroke();
268   
269   //sered prav
270   
271   context.lineWidth="3";
272     context.strokeStyle="#ffffff";
273     context.beginPath();
274     context.moveTo(300, 289);                                                                                                                                                         
275     context.lineTo(300,311 );
276     context.stroke();
277     
278   
279     }
280   
281 
282     // Запуск системы
283                       // добавляем 20 частиц, сдвинув их от стен
284     addNewBall(16*w/32, 16*h/32 );
285     addNewBall(16*w/32, 8*h/32 );  
286     addNewBall(16*w/32 - r,   8*h/32 - 1.7321*r);  
287     addNewBall(16*w/32 + r,   8*h/32 - 1.7321*r );
288     addNewBall(16*w/32,     8*h/32 - 2*1.7321*r );    
289     addNewBall(16*w/32 - 2*r,   8*h/32 - 2*1.7321*r );
290     addNewBall(16*w/32 + 2*r,   8*h/32 - 2*1.7321*r );
291     addNewBall(16*w/32 + r,   8*h/32 - 3*1.7321*r );
292     addNewBall(16*w/32 - r,   8*h/32 - 3*1.7321*r );
293     addNewBall(16*w/32 + 3*r,   8*h/32 - 3*1.7321*r );
294     addNewBall(16*w/32 - 3*r,   8*h/32 - 3*1.7321*r );
295     addNewBall(16*w/32,     8*h/32 - 4*1.7321*r );
296     addNewBall(16*w/32 - 2*r,   8*h/32 - 4*1.7321*r );
297     addNewBall(16*w/32 + 2*r,   8*h/32 - 4*1.7321*r );
298     addNewBall(16*w/32 - 4*r,   8*h/32 - 4*1.7321*r );
299     addNewBall(16*w/32 + 4*r,   8*h/32 - 4*1.7321*r );
300     addNewBall(16*w/32, 16*h/32 );  
301     
302   this.setSlider_01 = function(c) { q=-c ;}; // функция для слайдера угла
303   this.setSlider_02 = function(c) { v0=c ;}; // функция для слайдера угла
304 
305  // Настройка интерфейса
306 
307     slider_01.min = 0;               slider_01.max =360;
308     slider_01.step = 0.5;
309     slider_01.value = q;          // начальное значение ползунка должно задаваться после min и max
310     text_01.value = Math.abs(q);
311     slider_02.min = 0;               slider_02.max = 10;
312     slider_02.step = 0.5;
313     slider_02.value = v0;                // начальное значение ползунка должно задаваться после min и max
314     text_02.value = v0;
315   
316   this.setSlider_01(q);
317   this.setSlider_02(v0);
318     
319     this.newSystem = function() {
320     balls[0].vx = v0* Math.cos(q*Pi/180);
321         balls[0].vy = v0* Math.sin(q*Pi/180);
322   }
323 
324   this.newSystem1 = function() {
325   for (var i = 20; i >= 0; i--) 
326   {balls.splice(i, 1)};
327   addNewBall(16*w/32, 16*h/32 );
328     addNewBall(16*w/32, 8*h/32 );  
329     addNewBall(16*w/32 - r,   8*h/32 - 1.7321*r);  
330     addNewBall(16*w/32 + r,   8*h/32 - 1.7321*r );
331     addNewBall(16*w/32,     8*h/32 - 2*1.7321*r );    
332     addNewBall(16*w/32 - 2*r,   8*h/32 - 2*1.7321*r );
333     addNewBall(16*w/32 + 2*r,   8*h/32 - 2*1.7321*r );
334     addNewBall(16*w/32 + r,   8*h/32 - 3*1.7321*r );
335     addNewBall(16*w/32 - r,   8*h/32 - 3*1.7321*r );
336     addNewBall(16*w/32 + 3*r,   8*h/32 - 3*1.7321*r );
337     addNewBall(16*w/32 - 3*r,   8*h/32 - 3*1.7321*r );
338     addNewBall(16*w/32,     8*h/32 - 4*1.7321*r );
339     addNewBall(16*w/32 - 2*r,   8*h/32 - 4*1.7321*r );
340     addNewBall(16*w/32 + 2*r,   8*h/32 - 4*1.7321*r );
341     addNewBall(16*w/32 - 4*r,   8*h/32 - 4*1.7321*r );
342     addNewBall(16*w/32 + 4*r,   8*h/32 - 4*1.7321*r );
343     addNewBall(16*w/32, 16*h/32 );  
344   
345 }
346     setInterval(control, 1000 / fps);
347 }

Файл "Billyard1version.html" 

 1 <!DOCTYPE html>
 2 <html>
 3 <head>
 4     <title>Billyard</title>
 5     <script src="Billyard1version.js"></script>
 6 </head>
 7 <body>
 8      <canvas id="canvasBalls" width="300" height="600" style="border:1px none #000000;background: #008000"></canvas>
 9 <br>
10     <div>Угол:
11         <input type="range" id="slider_01" style="width: 150px;" oninput="app.setSlider_01(this.value); document.getElementById('text_01').value = this.value;">
12        q =
13         <input id="text_01" style="width: 5ex;" required pattern="[-+]?([0-9]*\.[0-9]+|[0-9]+)"  oninput="
14             // если введено не число - строка не пройдет валидацию по паттерну выше, и checkValidity() вернет false
15             if (!this.checkValidity()) return;
16             app.setSlider_01(this.value);
17             document.getElementById('slider_01').value = this.value;
18         ">
19     </div><br>
20 
21     <div>Начальная скорость:
22         <input type="range" id="slider_02" style="width: 150px;" oninput="app.setSlider_02(this.value); document.getElementById('text_02').value = this.value;">
23        v0 =
24         <input id="text_02" style="width: 5ex;" required pattern="[-+]?([0-9]*\.[0-9]+|[0-9]+)" oninput="
25             // если введено не число - строка не пройдет валидацию по паттерну выше, и checkValidity() вернет false
26             if (!this.checkValidity()) return;
27             app.setSlider_02(this.value);
28             document.getElementById('slider_02').value = this.value;
29         ">
30     </div><br> 
31   
32   
33   <input type="button" style="width: 50px" name="" onclick="app.newSystem();return false;" value="PLAY"/>
34   <input type="button" style="width: 50px" name="" onclick="app.newSystem1();return false;" value="AGAIN"/>
35   
36  <script type="text/javascript">var app = new MainBalls(
37             document.getElementById('slider_01'),
38             document.getElementById('text_01'),
39             document.getElementById('slider_02'),
40             document.getElementById('text_02')
41     );</script>
42 </body>
43 </html>


В реальности данная картина так же видна, хоть и не столь явно из-за неидеальности системы .



1.gif 


2.gif


3.gif

Обсуждение результатов и выводы[править]

В ходе работы над проектом была написана программа, моделирующая процесс игры в бильярд. Данная программа показывает, что траектория разлета шаров после центрального удара не зависит от силы удара, но зависит от малейшего изменения угла, так как меняется распространение ударной волны в пирамиде. При силе, достаточной для визуально заметного разлета шаров, при изменении угла на 1 градус - полное отклонение от симметрии, при 0.1 - заметное отклонение от симметрии, при 0.01 - трудно различимое.



Скачать отчет:docx

Ссылки по теме[править]

См. также[править]

Источник — «http://tm.spbstu.ru/?title=КП:_Динамика_бильярда&oldid=34483»