Корреляции перемещений в кристаллах (компьютерное моделирование) — различия между версиями
Wikiadmin (обсуждение | вклад) |
|||
| (не показано 6 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
Расчеты: [[Панченко Артём]] | Расчеты: [[Панченко Артём]] | ||
| − | == | + | == Треугольная кристаллическая решётка == |
| − | Рассматривается образец размерами 100x100 частиц, с периодическими граничными условиями, взаимодействие частиц описывается потенциалом Морзе с параметром <math>{\alpha}{a_0}=6</math>, учитывается взаимодействие с первой координационной сферой, начальная кинетическая энергия равна <math>{ | + | Рассматривается образец размерами 100x100 частиц, с периодическими граничными условиями, взаимодействие частиц описывается потенциалом Морзе с параметром <math>{\alpha}{a_0}=6</math>, учитывается взаимодействие с первой координационной сферой, начальная кинетическая энергия равна <math>{E_{kin}}=10^{-5}{D}</math>. Изменение параметров оговорено отдельно. |
| + | |||
| + | * Проведено сравнение с результатами экспериментов по рассеиванию электронов: [[media:Correlation effects among thermal displacements of atoms.pdf|T. Sakuma et al., Correlation effects among thermal displacements of atoms in Vse by diffuse neutron scattering measurement // J Thermal Anal Calorim, 99, 173-176 (2010)]] | ||
| + | |||
| + | * Результаты аналитического расчёта корреляции из статфизики приведены в статье: [[media:On the Interatomic Correlations and Mean Square....pdf|C. G. Rodrigues, M. F. Pascual and V. I. Zubovy, On the Interatomic Correlations and Mean Square Relative Atomic Displacements in an Anharmonic BCC Crystal // Brazilian Journal of Physics, vol. 27, no. 4, december, 1997]] | ||
Рассчитаны корреляции <math>\langle\mathbf{A}\mathbf{A}\rangle</math>, <math>\langle\mathbf{u}\mathbf{u}\rangle</math>, <math>\langle\mathbf{u}\mathbf{u}'\rangle</math> в системе координат связанных со связью и найдено среднее по всем связям, а затем усреднено по 10 рассчётам. Ось абсцисс направлена по связи, ось ординат перпендикулярно (векторное произведение оси абсцисс и вектора перпендикулярного плоскости). Тензоры диагональны с точностью <math>10^{-3}</math>. | Рассчитаны корреляции <math>\langle\mathbf{A}\mathbf{A}\rangle</math>, <math>\langle\mathbf{u}\mathbf{u}\rangle</math>, <math>\langle\mathbf{u}\mathbf{u}'\rangle</math> в системе координат связанных со связью и найдено среднее по всем связям, а затем усреднено по 10 рассчётам. Ось абсцисс направлена по связи, ось ординат перпендикулярно (векторное произведение оси абсцисс и вектора перпендикулярного плоскости). Тензоры диагональны с точностью <math>10^{-3}</math>. | ||
| + | |||
| + | <gallery widths=500px heights=330px perrow = 2> | ||
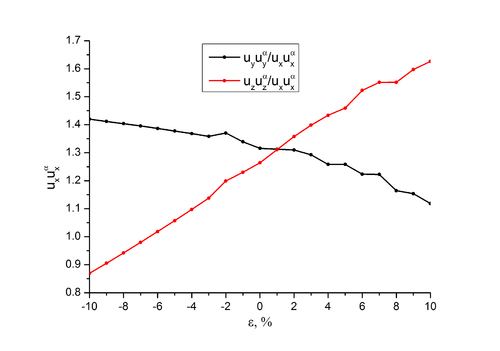
| + | Файл:uu_a___2D_Morse.png|Рис. 1.1. Зависимость диагональных компонент тензора <math>\mathbf{u}\mathbf{u_\alpha}</math> от номера расстояния. | ||
| + | Файл:AA_a_2D_Morse_systemsizeXdY.png|Рис. 1.2. Зависимость <math>\langle\mathbf{A}\mathbf{A}\rangle</math> от размера системы при кратном соотношении количества слоёв. | ||
| + | Файл:uu_a___3D_Morse_temperature.png|Рис. 1.3. Зависимость <math>\mathbf{u}\mathbf{u_\alpha}</math> от начальной кинетической энергии. | ||
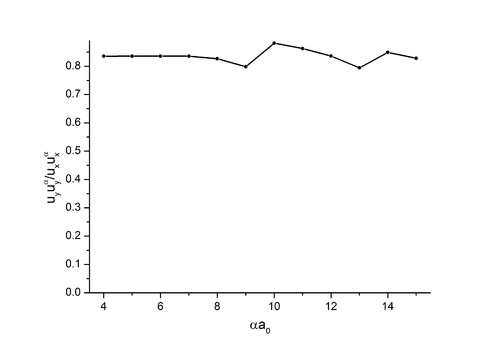
| + | Файл:uu_a___2D_Morse_alfa.png|Рис. 1.4. Зависимость <math>\langle\mathbf{u}\mathbf{u}'\rangle</math> от <math>{\alpha}{a_0}</math>. | ||
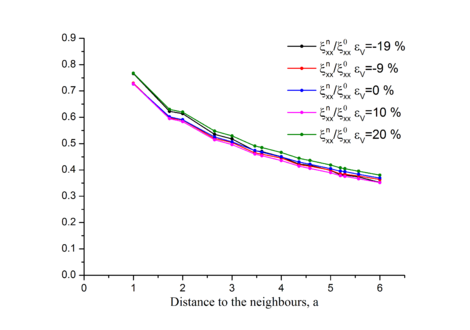
| + | Файл:uu_a___2D_Morse_epsion.png|Рис. 1.5. Зависимость <math>\langle\mathbf{u}\mathbf{u}'\rangle</math> от <math>\varepsilon</math>. | ||
| + | Файл:uu_a___2D_Morse_a_cut.png|Рис. 1.6. Зависимость <math>\langle\mathbf{u}\mathbf{u}'\rangle</math> от радиуса обрезания. | ||
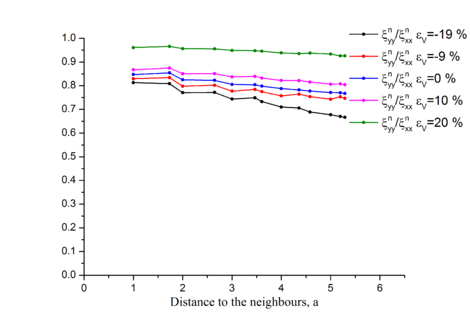
| + | Файл:uu_a___2D_Morse_YY_epsion.png|Рис. 1.7. Зависимость <math>\langle\mathbf{u}\mathbf{u}'\rangle</math> от <math>\varepsilon</math>. | ||
| + | </gallery> | ||
Результаты расчёта с приведёнными выше параметрами представлены на Рис.1.1. | Результаты расчёта с приведёнными выше параметрами представлены на Рис.1.1. | ||
| − | + | Размер системы выбран исходя из результатов представленных на Рис.1.2. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Из Рис.1.3, Рис.1.4, Рис.1.5, Рис.1.6 можно сделать вывод о слабой зависимости отношения продольных корреляций к дисперсии от <math>{E_{kin}}</math>, <math>{\alpha}{a_0}</math>, <math>{a_{cut}}</math>, <math>\varepsilon</math> и таким образом это отношение является фактически константой. | |
| − | + | Однако обнаружено влияние внешних напряжений (Рис.1.7) на отношение поперечной корреляции к продольной, таким образом мы можем сделать предположение, что это отношение зависит от внутренних напряжений. | |
| − | |||
| − | Однако обнаружено влияние внешних напряжений (Рис.1. | ||
| Строка 27: | Строка 35: | ||
Отношение перпендикулярной компоненты корреляции <math>\langle\mathbf{A}\mathbf{A}\rangle</math> к продольной уменьшается при растяжении, можно заметить слабое уменьшение отношение с ростом м (Рис.1.4). | Отношение перпендикулярной компоненты корреляции <math>\langle\mathbf{A}\mathbf{A}\rangle</math> к продольной уменьшается при растяжении, можно заметить слабое уменьшение отношение с ростом м (Рис.1.4). | ||
| − | Проведем анализ графиков Рис. 1.3 - 1.4 ([[А.М. Кривцов]]). | + | Проведем анализ графиков Рис. 1.3 - 1.4 ([[А.М. Кривцов]]), данный анализ проведён по старым графикам, однако значения на графиках фактически не изменились. |
{| class="wikitable" | {| class="wikitable" | ||
| Строка 90: | Строка 98: | ||
<br style="clear: both" /> | <br style="clear: both" /> | ||
| − | + | == ГЦК решетка == | |
| − | ==ГЦК== | ||
Рассчитаны корреляции <math>\mathbf{A}\mathbf{A_\alpha}</math>, <math>\mathbf{u}\mathbf{u}</math>, <math>\mathbf{u}\mathbf{u_\alpha}</math> в системе координат связанных со связью и найдено среднее по всем связям. Ось абсцисс направлена по связи, ось ординат перпендикулярно (по другой связи), ось аппликат по векторному произведению абсциссы и ординаты. Тензоры диагональны с точность <math>10^{-3}</math>. | Рассчитаны корреляции <math>\mathbf{A}\mathbf{A_\alpha}</math>, <math>\mathbf{u}\mathbf{u}</math>, <math>\mathbf{u}\mathbf{u_\alpha}</math> в системе координат связанных со связью и найдено среднее по всем связям. Ось абсцисс направлена по связи, ось ординат перпендикулярно (по другой связи), ось аппликат по векторному произведению абсциссы и ординаты. Тензоры диагональны с точность <math>10^{-3}</math>. | ||
| Строка 104: | Строка 111: | ||
[[Файл:uu_a___3D_Morse_alfa.png|500px|thumb|center|Рис. 1.2. Зависимость <math>\mathbf{u}\mathbf{u_\alpha}</math> от <math>{\alpha}{a_0}</math>.]] | [[Файл:uu_a___3D_Morse_alfa.png|500px|thumb|center|Рис. 1.2. Зависимость <math>\mathbf{u}\mathbf{u_\alpha}</math> от <math>{\alpha}{a_0}</math>.]] | ||
| − | |||
| − | |||
<br style="clear: both" /> | <br style="clear: both" /> | ||
| + | == См. также == | ||
| − | + | * [[Тепловое расширение кристаллов (компьютерное моделирование)]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Текущая версия на 14:56, 27 июля 2014
Расчеты: Панченко Артём
Треугольная кристаллическая решётка[править]
Рассматривается образец размерами 100x100 частиц, с периодическими граничными условиями, взаимодействие частиц описывается потенциалом Морзе с параметром , учитывается взаимодействие с первой координационной сферой, начальная кинетическая энергия равна . Изменение параметров оговорено отдельно.
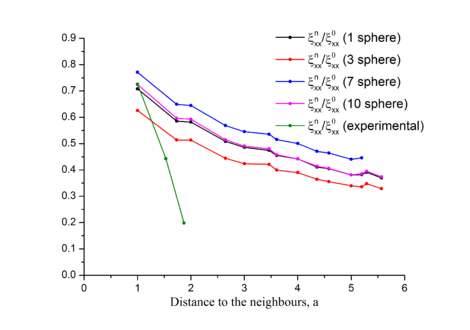
- Проведено сравнение с результатами экспериментов по рассеиванию электронов: T. Sakuma et al., Correlation effects among thermal displacements of atoms in Vse by diffuse neutron scattering measurement // J Thermal Anal Calorim, 99, 173-176 (2010)
- Результаты аналитического расчёта корреляции из статфизики приведены в статье: C. G. Rodrigues, M. F. Pascual and V. I. Zubovy, On the Interatomic Correlations and Mean Square Relative Atomic Displacements in an Anharmonic BCC Crystal // Brazilian Journal of Physics, vol. 27, no. 4, december, 1997
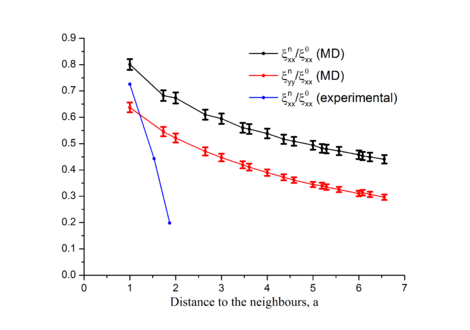
Рассчитаны корреляции , , в системе координат связанных со связью и найдено среднее по всем связям, а затем усреднено по 10 рассчётам. Ось абсцисс направлена по связи, ось ординат перпендикулярно (векторное произведение оси абсцисс и вектора перпендикулярного плоскости). Тензоры диагональны с точностью .
Результаты расчёта с приведёнными выше параметрами представлены на Рис.1.1.
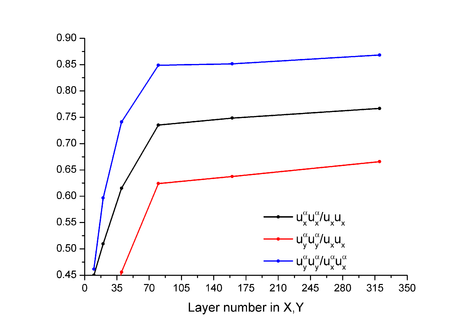
Размер системы выбран исходя из результатов представленных на Рис.1.2.
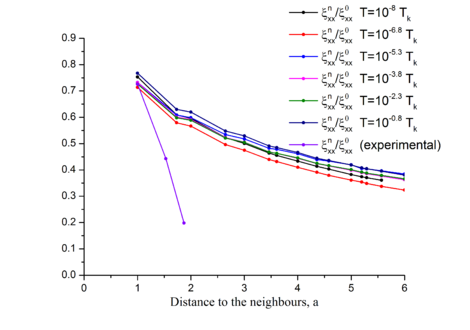
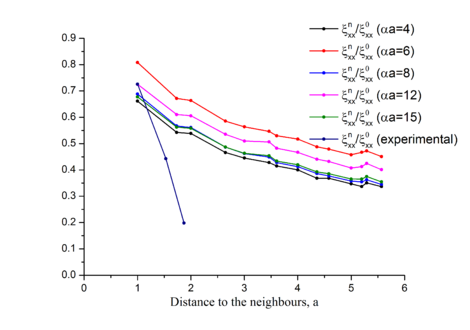
Из Рис.1.3, Рис.1.4, Рис.1.5, Рис.1.6 можно сделать вывод о слабой зависимости отношения продольных корреляций к дисперсии от , , , и таким образом это отношение является фактически константой.
Однако обнаружено влияние внешних напряжений (Рис.1.7) на отношение поперечной корреляции к продольной, таким образом мы можем сделать предположение, что это отношение зависит от внутренних напряжений.
Отношение перпендикулярной компоненты корреляции к продольной увеличивается при растяжении, и не имеет выраженной зависимости от (Рис.1.3).
Отношение перпендикулярной компоненты корреляции к продольной уменьшается при растяжении, можно заметить слабое уменьшение отношение с ростом м (Рис.1.4).
Проведем анализ графиков Рис. 1.3 - 1.4 (А.М. Кривцов), данный анализ проведён по старым графикам, однако значения на графиках фактически не изменились.
| Величина | Значения | Источник | Комментарий | ||
|---|---|---|---|---|---|
| -5% | 0 | 5% | Рис. 1.3 - 1.4 | деформация | |
| 1.48 | 1.42 | 1.36 | Рис. 1.4 | отношение поперечной составляющей тензора к продольной | |
| 0.810 | 0.825 | 0.840 | Рис. 1.3 | отношение поперечной составляющей тензора к продольной | |
| 0.716 | 0.706 | 0.692 | расчет | относительная продольная корреляция перемещений | |
| 0.580 | 0.582 | 0.582 | расчет | относительная поперечная корреляция перемещений | |
Связь параметров и определяется формулами
На основании данных таблицы можно сделать следующие выводы.
- В рассмотренном интервале деформаций (от -5% до 5%) зависимости величин и от деформаций можно считать линейными.
- Относительные корреляции и в рассматриваемом интервале деформаций меняются незначительно.
- Относительная поперечная корреляция несколько меньше, чем относительная продольная , что представляется разумным.
- Значения относительных корреляции и сравнимы с единицей — перемещения ближайших частиц сильно коррелируют. Есть основания полагать, что с увеличением числа частиц корреляции еще усилятся — необходимо указать, сколько частиц использовалось при расчете. Желательно проверить влияние числа частиц на результат. На корреляции могут также оказывать влияния термостаты, баростаты и т.д.
Отметим, что согласно формуле , тензор будет близок к шаровому () в одном из двух случаев:
- относительные корреляции малы: ;
- относительные корреляции близки: .
В рассматриваемом случае относительные корреляции не малы, и, хоть и не очень значительно, но различаются, что приводит к существенному отклонению формы тензора от шаровой ().
ГЦК решетка[править]
Рассчитаны корреляции , , в системе координат связанных со связью и найдено среднее по всем связям. Ось абсцисс направлена по связи, ось ординат перпендикулярно (по другой связи), ось аппликат по векторному произведению абсциссы и ординаты. Тензоры диагональны с точность .
При отсутствии внешних напряжений зависимость от ширины потенциальной ямы для потенциала морзе отсутствует (Рис.1.1).
При постоянной ширине потенциальной ямы компоненты зависят от гидростатической деформации линейно, при этом компонента с расширением убывает, а возрастает (Рис.1.2).