Гексогональная плотноупакованная решетка — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
м (переименовал ГПУ в Гексогональная плотноупакованная решетка) |
(→Структура решетки) |
||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 1: | Строка 1: | ||
[[Category: Кристаллические решетки]] | [[Category: Кристаллические решетки]] | ||
| + | |||
| + | [[Файл: gpu.png|thumb|]] | ||
| + | |||
| + | ==Структура решетки== | ||
| + | Гексагональная плотноупакованная решетка, сокращенно ГПУ, отличается от простой гексагональной тем, что в центр объема каждой второй треугольной призмы помещен дополнительный узел. При этом весь кристалл оказывается составлен из правильных тетраэдров. Это накладывает строгое условие на соотношение между высотой призмы <math>c</math> и длиной ее основания <math>a</math>: <math>c/a = \sqrt{8/3}\approx 1{,}633</math>. Хотя решетки с другим близким к этому значением <math>c/a</math> часто рассматривают как слабодеформированный вариант ГПУ. | ||
| + | |||
| + | ==Орты образующие решетку== | ||
| + | <math>\textbf{n}_{1,4}=\pm \textbf{i}, | ||
| + | \quad \textbf{n}_{8,11}=\frac{\sqrt{3}}{3} \textbf{j}\pm\frac{\sqrt{3}}{6}\textbf{k},\quad\textbf{n}_{2,3,5,6,}=\pm\frac{1}{2}\textbf{i}\pm\frac{\sqrt{3}}{2}\textbf{j},\quad\textbf{n}_{7,9,10,12}=\pm\frac{1}{2}\textbf{i}\ - \frac{\sqrt{3}}{6}\textbf{j}\pm\frac{\sqrt{6}}{3}\textbf{k} | ||
| + | </math>[[Category: Кристаллические решетки]] | ||
Текущая версия на 12:34, 10 марта 2022
Структура решетки[править]
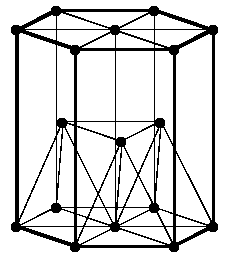
Гексагональная плотноупакованная решетка, сокращенно ГПУ, отличается от простой гексагональной тем, что в центр объема каждой второй треугольной призмы помещен дополнительный узел. При этом весь кристалл оказывается составлен из правильных тетраэдров. Это накладывает строгое условие на соотношение между высотой призмы и длиной ее основания : . Хотя решетки с другим близким к этому значением часто рассматривают как слабодеформированный вариант ГПУ.
Орты образующие решетку[править]