КП: Гравитационный коллапс — различия между версиями
Test (обсуждение | вклад) |
Test (обсуждение | вклад) |
||
| (не показано 5 промежуточных версий 3 участников) | |||
| Строка 18: | Строка 18: | ||
== Общие сведения по теме == | == Общие сведения по теме == | ||
| + | [http://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%B2%D1%81%D0%B5%D0%BC%D0%B8%D1%80%D0%BD%D0%BE%D0%B3%D0%BE_%D1%82%D1%8F%D0%B3%D0%BE%D1%82%D0%B5%D0%BD%D0%B8%D1%8F Закон всемирного тяготения]<br> | ||
| + | [http://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%82%D0%B5%D0%BD%D1%86%D0%B8%D0%B0%D0%BB_%D0%9B%D0%B5%D0%BD%D0%BD%D0%B0%D1%80%D0%B4-%D0%94%D0%B6%D0%BE%D0%BD%D1%81%D0%B0 Потенциал Леннард-Джонса]<br> | ||
| + | [http://ru.wikipedia.org/wiki/%D0%92%D1%82%D0%BE%D1%80%D0%BE%D0%B9_%D0%B7%D0%B0%D0%BA%D0%BE%D0%BD_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%D0%B0 Второй закон Ньютона]<br> | ||
| + | |||
| + | Расчет сил осуществляется следующим образом | ||
| + | |||
| + | <math>f(r, \dot{r}) = \frac{A_1}{r^2} + \frac{A_2}{r^{13}} + \frac{A_3\dot{r}}{r^{14}}</math><br> | ||
| + | |||
| + | |||
| + | <math>F_i = \sum_{j}f(r, \dot{r})\frac{\underline{r_j} - \underline{r_i}}{|\underline{r_j} - \underline{r_i}|}</math> | ||
== Решение == | == Решение == | ||
| + | [https://bitbucket.org/Pasha123/points репозиторий] | ||
| + | |||
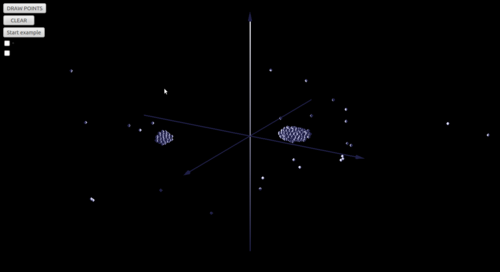
| + | Была написана программа для моделирования системы при небольших значениях N (при больших N резко увеличивается количество вычислений и необходимо применять специальные алгоритмы расчета, что не входит в данную работу).<br> | ||
| + | В программе можно задавать геометрические параметры облака частиц, угловую скорость облака и максимальный модуль хаотической скорости частиц. Последние две величины задаются с помощью безразмерных коэффициентов отношения к равновесным угловой и линейной скоростям частицы, являющейся спутником материальной точки с массой, равной суммарной массе всех частиц. | ||
| − | = | + | {{#widget:YouTube|id=X6n6ZopwQGM}} |
| − | == | + | == Результаты == |
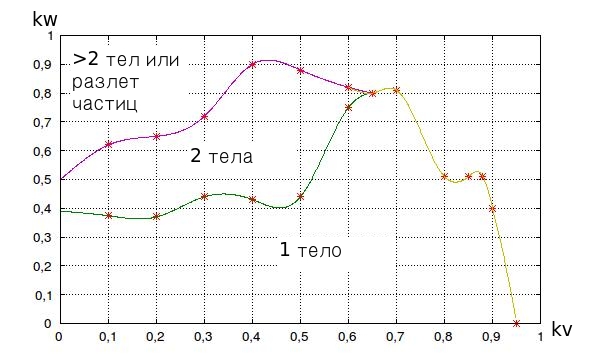
| + | С помощью написанной программы была найдена область параметров для образования двух тел. Найденные точки были интерполированы кубическими сплайнами. | ||
| + | [[Файл:Result1.jpeg|800px]] | ||
== См. также == | == См. также == | ||
| Строка 30: | Строка 46: | ||
* [[Курсовые проекты ТМ 2013|Курсовые проекты 2013]] | * [[Курсовые проекты ТМ 2013|Курсовые проекты 2013]] | ||
* [[Курсовые проекты ТМ 2012|Курсовые проекты 2012]] | * [[Курсовые проекты ТМ 2012|Курсовые проекты 2012]] | ||
| − | |||
[[Category: Студенческие проекты]] | [[Category: Студенческие проекты]] | ||
Текущая версия на 09:18, 28 мая 2014
А.М. Кривцов > Теоретическая механика > Курсовые проекты 2014 > Гравитационный коллапсКурсовой проект по Теоретической механике
Исполнитель: Поцелуев Павел
Группа: 08 (23604)
Семестр: весна 2014
Содержание
Аннотация проекта[править]
В данном проекте изучается поведение системы, состоящей из N частиц, взаимодействие которых состоит из сил гравитационного притяжения, сил отталкивания и диссипативных сил
Постановка задачи[править]
- написать программу, моделирующую систему из N частиц
- найти область начальных параметров системы, для которой происходит образование двух тел
Общие сведения по теме[править]
Закон всемирного тяготения
Потенциал Леннард-Джонса
Второй закон Ньютона
Расчет сил осуществляется следующим образом
Решение[править]
Была написана программа для моделирования системы при небольших значениях N (при больших N резко увеличивается количество вычислений и необходимо применять специальные алгоритмы расчета, что не входит в данную работу).
В программе можно задавать геометрические параметры облака частиц, угловую скорость облака и максимальный модуль хаотической скорости частиц. Последние две величины задаются с помощью безразмерных коэффициентов отношения к равновесным угловой и линейной скоростям частицы, являющейся спутником материальной точки с массой, равной суммарной массе всех частиц.
Результаты[править]
С помощью написанной программы была найдена область параметров для образования двух тел. Найденные точки были интерполированы кубическими сплайнами.