Конечно-элементное моделирование гидродинамических нагрузок на упругие тела при погружении в жидкость — различия между версиями
(→Исследование гидродинамических нагрузок) |
|||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 41: | Строка 41: | ||
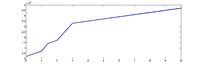
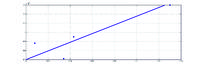
Рассмотрим графики на рис.6 и 7. Видно, что стальной шар отскакивает от упругого основания, при этом высота отскока приблизительно 0.04 м, а скорость сразу после отскока составляла 1 м/с. Весь процесс от касания шара поверхности жидкости до полного затухания системы длится 0.38 с. | Рассмотрим графики на рис.6 и 7. Видно, что стальной шар отскакивает от упругого основания, при этом высота отскока приблизительно 0.04 м, а скорость сразу после отскока составляла 1 м/с. Весь процесс от касания шара поверхности жидкости до полного затухания системы длится 0.38 с. | ||
Отклонения экспериментальной кривой на графиках выше вызвано погрешностью программы, производящей отслеживание движения тела. | Отклонения экспериментальной кривой на графиках выше вызвано погрешностью программы, производящей отслеживание движения тела. | ||
| − | [[Файл: Ershov6.jpg|200px|thumb|right| Рис.6. V(t) для стального шарика]] | + | [[Файл: Ershov6.jpg|200px|thumb|right| Рис.6. V(t) для стального шарика]]n/ |
[[Файл: Ershov7.jpg|200px|thumb|right| Рис.7. U(t) для стального шарика]] | [[Файл: Ershov7.jpg|200px|thumb|right| Рис.7. U(t) для стального шарика]] | ||
| Строка 49: | Строка 49: | ||
=Исследование гидродинамических нагрузок= | =Исследование гидродинамических нагрузок= | ||
| − | [[Файл: Ershov8.jpg|200px|thumb| | + | [[Файл: Ershov8.jpg|200px|thumb|left| Рис.8. Зависимость контактного давления от начальной скорости]] [[Файл: Ershpv9.jpg|200px|thumb|left| Рис.9. Зависимость контактного давления от времени]] |
На основе полученной численной модели необходимо исследовать изменение контактного давления в зависимости от вертикальной скорости, с которой твёрдое тело падает в жидкость. Расчет проводится для скоростей 0 м/с, 1 м/с, 1.4 м/с, 2 м/с, 3 м/с, 10 м/с. Контактное давление измеряется в точке первого касания поверхности жидкости и твердого тела. Результаты проведенных расчетов представлены на рис. 18. Из графика видно, что по мере увеличения вертикальной скорости, контактное давление возрастает. Для случая, когда начальная скорость 1 м/с, можно построить график изменения контактного давлением со временем, в начальный момент времени происходит касание твердым телом поверхности жидкости (см. рис.19). Исходя из порядкового совпадения экспериментальной и численной моделей, можно сделать вывод, что полученные графики на рис. 8 – предполагаемый вид изменения контактного давления для рассматриваемого процесса в зависимости от скорости падения. Зависимость контактного давления от времени | На основе полученной численной модели необходимо исследовать изменение контактного давления в зависимости от вертикальной скорости, с которой твёрдое тело падает в жидкость. Расчет проводится для скоростей 0 м/с, 1 м/с, 1.4 м/с, 2 м/с, 3 м/с, 10 м/с. Контактное давление измеряется в точке первого касания поверхности жидкости и твердого тела. Результаты проведенных расчетов представлены на рис. 18. Из графика видно, что по мере увеличения вертикальной скорости, контактное давление возрастает. Для случая, когда начальная скорость 1 м/с, можно построить график изменения контактного давлением со временем, в начальный момент времени происходит касание твердым телом поверхности жидкости (см. рис.19). Исходя из порядкового совпадения экспериментальной и численной моделей, можно сделать вывод, что полученные графики на рис. 8 – предполагаемый вид изменения контактного давления для рассматриваемого процесса в зависимости от скорости падения. Зависимость контактного давления от времени | ||
| − | + | =Выводы= | |
| − | |||
| − | |||
Проведена верификация конечно-элементного подхода Лагранжа-Эйлера (CEL) на примере задачи об истечении жидкости из малого бокового отверстия. | Проведена верификация конечно-элементного подхода Лагранжа-Эйлера (CEL) на примере задачи об истечении жидкости из малого бокового отверстия. | ||
Текущая версия на 21:59, 20 июня 2013
Выполнил: Ершов Дмитрий Сергеевич
Научный руководитель: Шубин Сергей Николаевич
Страница в разработке
Содержание
Введение[править]
В данной работе рассматривается вертикальный удар абсолютно твердого тела о жидкость. Такая постановка возникает, например, при расчете на прочность морских конструкций, опускаемых в воду с корабля. При погружении произвольного тела в жидкость характер распределения гидродинамического давления по смоченной поверхности тела, а также его величина определяются многими факторами: начальной скоростью удара, углом входа, массой и формой тела, условиями воздушной и жидкой сред в момент контакта поверхностей, упругостью тела и другими факторами. Решение таких задач представляют большие математические трудности, которые обусловлены неустановившимся характером движения жидкости при погружении тела, нелинейностью условий, а также струйными явлениями и брызгообразованием, приводящими к разрывным движениям. Целью данной работы является получение математической модели с применением конечно-элементного подхода Лагранжа-Эйлера(CEL) в Abaqus/Explicit для задачи о вертикальном ударе абсолютно твердого тела о жидкость и его погружении. Также будет проведен анализ полученной модели и ее сравнение с результатами натурного эксперимента, проведенного в рамках данной работы. На заключительном этапе будет представлено исследование гидродинамических нагрузок, возникающих при контакте жидкости и твердого тела в зависимости от начальной скорости тела.
Цель работы[править]
Целью данной работы является получение математической модели с применением конечно-элементного подхода Лагранжа-Эйлера(CEL) в Abaqus/Explicit для задачи о вертикальном ударе абсолютно твердого тела о жидкость и его погружении. Также будет проведен анализ полученной модели и ее сравнение с результатами натурного эксперимента, проведенного в рамках данной работы. На заключительном этапе будет представлено исследование гидродинамических нагрузок, возникающих при контакте жидкости и твердого тела в зависимости от начальной скорости тела.
Постановка трехмерной задачи[править]
Рассматривается объем в виде прямоугольного параллелепипеда со сторонами 0.3х0.2х0.2 м, заполненный невязкой сжимаемой жидкостью с плотностью ρ=1000 кг/м^3 .. Объем ограничен боковой поверхностью и в нижнем основании стенками из органического стекла (ППМА). Высота стенок боковой поверхности выбирается таким образом, что жидкость не выливается через края при возникновении возмущений (см. рис.7). В рассматриваемый объем вертикально падает абсолютно твердое тело. Для него задана начальная скорость V_0 – скорость твердого тела в момент соприкосновения с поверхностью жидкости. В качестве твердых тел решено взять стальные шары с диаметрами 0.04м, 0.025м, хромированные стальные шары диаметром 0.03м и 0.015м и шар для настольного тенниса диаметром 0.04м. Свойства материала стали: ρ=7800 кг/м^3 ,E=2.1*〖10〗^11 Н/м^2 ,υ=0.3. Шар для настольного тенниса имеет массу 2.7 г, при моделировании описывается как жесткое тело без учета свойств материала. Рассматриваемое время расчета динамической задачи составляет 1 сек. Жидкость в системе моделируется с использованием подхода Эйлера, количество кубических конечных элементов варьируется от 10000 до 500.000. Абсолютно твердое тело описывается подходом Лагранжа с разбиением от 37 до 360 элементов. Выбор количества элементов разбиения в каждом моделировании является компромиссом между длительностью времени расчета и желаемой точностью получаемых результатов, учитывая исследование сходимости. Таким образом, в данном подразделе описана установка, заданы ее параметры и свойства определяющих ее материалов, а также подход для моделирования и расчетное количество элементов разбиения.
Сравнение эксперимента и моделирования[править]
Для численного трехмерного моделирования проводится расчет вертикального падения теннисного шара в жидкость со скоростью 3.75 м/с и ряд расчетов для стального шара для разных начальных скоростей. В ходе выполнения численного эксперимента получены результаты для падения теннисного шара со скоростью 3.75 м/с и стального шара со скоростью 1.4 м/с.
Для начала стоит качественно оценить полученные данные. На рис. 2 представлено визуальное сравнение моделирования и эксперимента для стального шара в одинаковые моменты времени. В случае моделирования отчетливо видно, что происходит формирование такой же каверны, как на видео эксперимента, положение шара совпадает на обоих изображениях. Однако, в модели присутствует одно существенное допущение, которое дает качественное отличие результатов. При моделировании не было учтено влияние воздуха на систему. Вследствие этого, при моделировании не видны кавитации, возникающие при столкновении шарика с основанием. Данное допущение возможно с учетом того, что мы рассматриваем шарообразное тело, имеющее относительно небольшой размер, поэтому отсутствие кавитаций не будут оказывать существенное влияние на порядковые показатели. В случае теннисного шарика также будет видно качественное совпадение (см. рис.3).
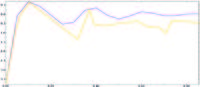
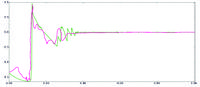
Получив совпадение на качественном уровне, необходимо убедиться в том, что модель дает порядковые совпадения с экспериментом. Для этого необходимо сравнить полученные при помощи пакета ProAnalyst численные результаты натурного эксперимента и моделирования. В ходе количественного сравнения результатов численного моделирования и натурного эксперимента построены графики изменения скоростей и перемещений в зависимости от времени для обоих тел. На рис.4 и рис.6 по вертикальной оси- скорость, м/с; по горизонтальной- время, с. На рис.5 и рис.7 по вертикальной оси - перемещение, м; по горизонтальной- время, с.
Из графика на рис. 4 видно, что теннисный шар, падая со скоростью 3.75 м/с погружается на ¾ своего диаметра, после этого вылетает на такое же расстояние. Погружаясь второй раз, тело опускается в воду чуть менее, чем на половину диаметра, при этом видно, что колебания затухают через секунду после падения шарика. Сравнивая кривые, представленные на графике, можно увидеть, что имеется совпадение значений перемещений в соответствующем промежутке времени: наибольшая глубина погружения 0.03 м и наибольшая высота отскока при отрыве от поверхности жидкости 0.03 м. Количественные совпадения натурного эксперимента и моделирования для теннисного шара также видны из анализа скорости на рис. 5.
Рассмотрим графики на рис.6 и 7. Видно, что стальной шар отскакивает от упругого основания, при этом высота отскока приблизительно 0.04 м, а скорость сразу после отскока составляла 1 м/с. Весь процесс от касания шара поверхности жидкости до полного затухания системы длится 0.38 с. Отклонения экспериментальной кривой на графиках выше вызвано погрешностью программы, производящей отслеживание движения тела.
n/
Подводя итог, из графиков видно, что в обоих случаях исследуемых тел значения для скоростей и перемещений имеют отклонения в рамках допустимой погрешности, можно говорить о совпадении проведенного моделирования и эксперимента.
Из полученных графиков и визуальной картины сравнения можно сделать вывод о корректной настройке модели для данной постановки (выбор размера элемента, определение свойств контакта, задание граничных условий и других параметров).
Исследование гидродинамических нагрузок[править]
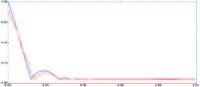
На основе полученной численной модели необходимо исследовать изменение контактного давления в зависимости от вертикальной скорости, с которой твёрдое тело падает в жидкость. Расчет проводится для скоростей 0 м/с, 1 м/с, 1.4 м/с, 2 м/с, 3 м/с, 10 м/с. Контактное давление измеряется в точке первого касания поверхности жидкости и твердого тела. Результаты проведенных расчетов представлены на рис. 18. Из графика видно, что по мере увеличения вертикальной скорости, контактное давление возрастает. Для случая, когда начальная скорость 1 м/с, можно построить график изменения контактного давлением со временем, в начальный момент времени происходит касание твердым телом поверхности жидкости (см. рис.19). Исходя из порядкового совпадения экспериментальной и численной моделей, можно сделать вывод, что полученные графики на рис. 8 – предполагаемый вид изменения контактного давления для рассматриваемого процесса в зависимости от скорости падения. Зависимость контактного давления от времени
Выводы[править]
Проведена верификация конечно-элементного подхода Лагранжа-Эйлера (CEL) на примере задачи об истечении жидкости из малого бокового отверстия. Разработана настраиваемая численная модель процесса вертикального падения абсолютно твердого тела в невязкую сжимаемую жидкость. Были получены уточненные экспериментальные данные процесса, подтверждающие порядковую и качественную объективность математического моделирования. На основе модели был получен предполагаемый вид зависимости контактного давления от скорости твердого тела в момент удара о жидкость. Для подтверждения предложенного способа определения гидродинамических нагрузок по полученной математической модели необходимо в будущем провести уточненное сравнение с аналитическими решениями для получения порядкового совпадения. Для совершенствования численной модели необходимо взять в рассмотрение влияние воздуха на систему, а также силу поверхностного натяжения воды. Более того, важно добиться повышения производительности программы.