КП: Моделирование образования Земли и Луны в газопылевом облаке с учётом солнечного притяжения(моделирование эллипсоида) — различия между версиями
Руслан (обсуждение | вклад) (→Решение) |
Руслан (обсуждение | вклад) (→Обсуждение результатов и выводы) |
||
| (не показано 19 промежуточных версий этого же участника) | |||
| Строка 12: | Строка 12: | ||
== Аннотация проекта == | == Аннотация проекта == | ||
| − | В основу данного курсового проекта положен [[Проект "Земля - Луна"|проект "Земля-Луна"]], выполненный [[А.М.Кривцов]]ым и [[Ле-Захаров А.А.|А.А | + | В основу данного курсового проекта положен [[Проект "Земля - Луна"|проект "Земля-Луна"]], выполненный [[А.М.Кривцов]]ым и [[Ле-Захаров А.А.|А.А. Ле-Захаровым]]. Исследуется возможное появление Солнечной системы из газопылевого облака путем моделирования облака (эллипсоида) частиц в силовом поле массивного центрального тела (Солнца), которое расположено в центре системы. |
| + | |||
== Постановка задачи == | == Постановка задачи == | ||
| − | Смоделировать систему облака частиц в центральном поле массивного тела (Солнца). Оценить правдоподобность гипотезы о появлении Солнечной системы из газопылевого облака. | + | Смоделировать систему облака частиц в центральном поле массивного тела (Солнца). Оценить правдоподобность гипотезы [http://elementy.ru/trefil/21175| о появлении Солнечной системы из газопылевого облака]. |
| + | |||
== Общие сведения по теме == | == Общие сведения по теме == | ||
| − | Внесение массивного центрального тела влечет за собой необходимость | + | Внесение массивного центрального тела влечет за собой необходимость пересчета начальных данных, в частности угловой скорости вращения облака <math>\omega</math>. Это имеет важное значение в дальнейшем исследовании, так как интуитивно понятно, что, если задать её слишком маленькой, получится так, что все частицы "упадут" на Солнце. Если выбрать её слишком большой, то получится так, что все частицы разлетятся. Значит, существует интервал значений угловой скорости, при которых облако будет стабильно вращаться и появится возможность образования кластеров. Моделирование при различных угловых скоростях подтверждает эти предположения. |
| + | |||
== Решение == | == Решение == | ||
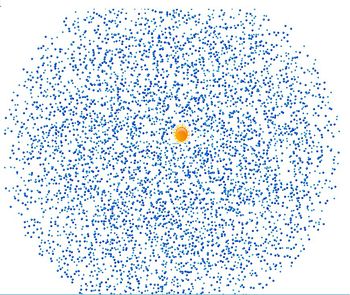
| − | + | [[Файл:NachUslLapiRuslan.jpg|thumb|350px|Начальное состояние, 10 тысяч частиц]] | |
| + | |||
| + | Начальными условиями в данной задаче являются следующие характеристики системы: | ||
| + | |||
| + | <math>N</math> — число частиц | ||
| + | |||
| + | <math>d_o</math> — среднее расстояние между частицами | ||
| + | |||
| + | <math>m</math> — масса частицы | ||
| + | |||
| + | <math>\frac{mN}{M}</math> — отношение массы системы, к массе массивного тела | ||
| + | |||
| + | <math>\frac{V_{xy}}{V}</math> — отношение рандомной составляющей скорости к линейной скорости вращения | ||
| + | |||
| + | |||
| + | Без учета солнца на частицу действуют следующие силы: | ||
| + | |||
| + | <math>\overline{F} = \overline{F}_{gr} + \overline{F}_{dis} + \overline{F}_{react}</math> | ||
| + | |||
| + | где <math>F_{gr} = - G\frac{m^2}{r^2}</math> гравитационная составляющая. | ||
| + | |||
| + | <math>F_{dis} = -G\frac{m^{2}a^{11}\beta r'}{r^{14}}</math> диссипативная составляющая. | ||
| + | |||
| + | <math>F_{react} = G\frac{m^{2}a^{11}}{r^{13}}</math> реактивная составляющая. | ||
| + | |||
| + | а <math>G</math> -гравитационная постоянная. | ||
| + | |||
| + | <math>m</math> - масса частицы | ||
| + | |||
| + | <math>a</math> - равновесное расстояние | ||
| + | |||
| + | <math>r</math> - расстояние между частицами | ||
| + | |||
| + | <math>\beta</math> - коэффициент диссипации | ||
| + | |||
При внесении массивного тела массы <math>M</math>, возникает центральное поле и на частицы начинает действовать сила | При внесении массивного тела массы <math>M</math>, возникает центральное поле и на частицы начинает действовать сила | ||
| Строка 43: | Строка 80: | ||
== Обсуждение результатов и выводы == | == Обсуждение результатов и выводы == | ||
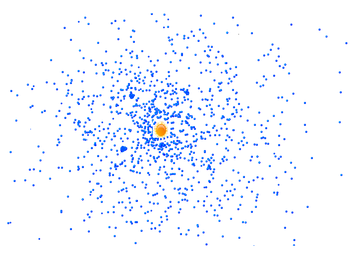
| − | В результате моделирования получилось стабильное облако частиц, которое вращается вокруг солнца. Начали образовываться небольшие кластеры, что свидетельствует о правильности модели и метода моделирования. Далее возможно исследование системы в зависимости от начальных параметров. Например увеличение числа частиц, изменение скоростей частиц, и наблюдение как будут меняться результаты. | + | [[Файл:ResultLapinRuslan.bmp|thumb|350px|10 тысяч частиц, результат после 15 тысяч итераций ]] |
| + | |||
| + | В результате моделирования получилось стабильное облако частиц, которое вращается вокруг солнца. Начали образовываться небольшие кластеры, что свидетельствует о правильности модели и метода моделирования. Далее возможно исследование системы в зависимости от начальных параметров. Например, увеличение числа частиц, изменение скоростей частиц, и наблюдение за тем, как будут меняться результаты. | ||
| + | |||
| + | Параллельно моделированию был проведен [[КП: Динамика молекулы (расчет)|аналитический анализ данной задачи]]. В дальнейшем планируется подведение результатов моделирования к аналитическим. | ||
| + | |||
== Ссылки по теме == | == Ссылки по теме == | ||
[[Проект "Земля - Луна"]] | [[Проект "Земля - Луна"]] | ||
Текущая версия на 14:52, 28 мая 2013
А.М. Кривцов > Теоретическая механика > Курсовые проекты 2013 > Моделирование образования Земли и Луны в газопылевом облаке с учётом солнечного притяжения (моделирование эллипсоида)Курсовой проект по Теоретической механике
Исполнитель: Лапин Руслан
Группа: 07 (20510)
Семестр: весна 2013
Содержание
Аннотация проекта[править]
В основу данного курсового проекта положен проект "Земля-Луна", выполненный А.М.Кривцовым и А.А. Ле-Захаровым. Исследуется возможное появление Солнечной системы из газопылевого облака путем моделирования облака (эллипсоида) частиц в силовом поле массивного центрального тела (Солнца), которое расположено в центре системы.
Постановка задачи[править]
Смоделировать систему облака частиц в центральном поле массивного тела (Солнца). Оценить правдоподобность гипотезы о появлении Солнечной системы из газопылевого облака.
Общие сведения по теме[править]
Внесение массивного центрального тела влечет за собой необходимость пересчета начальных данных, в частности угловой скорости вращения облака . Это имеет важное значение в дальнейшем исследовании, так как интуитивно понятно, что, если задать её слишком маленькой, получится так, что все частицы "упадут" на Солнце. Если выбрать её слишком большой, то получится так, что все частицы разлетятся. Значит, существует интервал значений угловой скорости, при которых облако будет стабильно вращаться и появится возможность образования кластеров. Моделирование при различных угловых скоростях подтверждает эти предположения.
Решение[править]
Начальными условиями в данной задаче являются следующие характеристики системы:
— число частиц
— среднее расстояние между частицами
— масса частицы
— отношение массы системы, к массе массивного тела
— отношение рандомной составляющей скорости к линейной скорости вращения
Без учета солнца на частицу действуют следующие силы:
где гравитационная составляющая.
диссипативная составляющая.
реактивная составляющая.
а -гравитационная постоянная.
- масса частицы
- равновесное расстояние
- расстояние между частицами
- коэффициент диссипации
При внесении массивного тела массы , возникает центральное поле и на частицы начинает действовать сила
, где - масса частицы, - расстояние до частицы.
Для равномерного движения по окружности частица должна иметь угловую скорость, такую чтобы
То есть угловая скорость от появления центрального тела, должна быть
А тогда учитывая еще и твердотельное вращение получаем искомую угловую скорость
где
составляющая возникающая из-за присутствия твердотельного вращения (частицы движутся, как твердое тело).
Обсуждение результатов и выводы[править]
В результате моделирования получилось стабильное облако частиц, которое вращается вокруг солнца. Начали образовываться небольшие кластеры, что свидетельствует о правильности модели и метода моделирования. Далее возможно исследование системы в зависимости от начальных параметров. Например, увеличение числа частиц, изменение скоростей частиц, и наблюдение за тем, как будут меняться результаты.
Параллельно моделированию был проведен аналитический анализ данной задачи. В дальнейшем планируется подведение результатов моделирования к аналитическим.