КП: Динамика молекулы (моделирование) — различия между версиями

Текущая версия на 12:54, 3 июня 2013

Курсовой проект по Теоретической механике

Исполнитель: Марков Николай

Группа: 07 (20510)

Семестр: весна 2013

Аннотация проекта[править]

Данный проект является продолжением работы над проектом "Земля-Луна"[1]. Исследуется поведение газопылевого облака в гравитационном поле, создаваемом Солнцем. Уже получены результаты для облака, имеющего форму эллипсоида. Результатом является образование двойной системы путём одновременного возникновения двух небесных тел, одно из которых в несколько раз больше другого по размеру. Для этого случая были проведены исследования, которые выявили наиболее оптимальные начальные данные, при которых образование двойной системы происходит с большой вероятностью.

Постановка задачи[править]

Выполнить моделирование динамики газопылевого облака, заданного виде тора в гравитационном поле центрального тела, с получением двойной системы, которая по своим характеристикам была приближена к системе Земля-Луна, а так же получить значения начальных параметров, при котором возникновение такой системы было бы наиболее вероятным.

Общие сведения по теме[править]

Для рассматриваемого случая необходимо учитывать многое из того, что не учитывается в случае, когда облако задается в виде эллипсоида. Скорость твердотельного вращения должна считаться исходя из факта влияния на облако как самих частиц,его составляющих, так и центрального тела. Таким образом, задав скорость вращения облака, можно добиться того, что частицы пыли не будут падать в центр или разлетаться.

Сила взаимодействия складывается из трех составляющих: гравитационного притяжения, реактивного отталкивания и диссипативных сил. Она зависит от расстояния между частицами и скорости их сближения. Диссипативная составляющая появляется из-за предположения, что нагретая частица интенсивно испускает газообразное вещество. Таким образом, каждая частица окружена газовой оболочкой. Потери энергии при взаимодействии этих оболочек и обуславливают появление диссипативной силы.

Облако в виде тора в поле центрального тела.

Также необходимо учитывать тот факт, что из-за более сложной геометрии тора по сравнению с геометрией эллипсоида, понять где и как будут образовываться необходимые кластеры гораздо сложнее. В случае с эллипсоидом, можно было предполагать образование системы в центральной части, тогда как для тора оно может произойти где угодно. Причем в данном случае может получиться так, что образуется несколько кластеров, подобных друг другу. Таким образом, для вероятности образования двойной системы, необходимо увеличивать толщину тора.

В качестве начальных данных, которые и задают систему в начальный момент времени и со значениями которых необходимо проводить эксперименты в первую очередь, берутся величины:

[math]N[/math] — число частиц

[math]d_{0}[/math] — среднее расстояние между частицами

[math] E_{hR}[/math] — соотношение радиуса тора к его толщине

[math]\frac{\omega_{0}}{\omega_{s}}[/math] — отношение угловых скоростей, задающее начальную скорость вращения облака

[math]\frac{V_{xy}}{V}[/math] — задание хаотической составляющей скорости по отношению к скорости, полученной из значения угловой скорости вращения, т.е.скорости вращения.

[math]\frac{M_{0}}{M}[/math] — отношение массы системы к массе центрального тела.

Решение[править]

Для решения данной задачи было проведено ознакомление и изучение результатов, полученных без учета центрального тела для эллипсоида,а так же разбор работы программы, производящей моделирование. Создана модель газопылевого облака в виде тора, а так же исследовано влияние начальной скорости вращения на устойчивость геометрии тора. Рассмотрим решение подробнее:

Пусть имеется частица, имеющая массу [math]m_{0}[/math], скорость [math]V_{0}[/math] и находящаяся на расстоянии [math]R[/math] от центрального тела массы [math]M[/math] . Тогда уравнение [math]m_{0} a =\ F[/math] будет иметь вид:

[math] \frac{m_{0}V_{0}^2}{R_{0}} =\ G\frac{m_{0}M}{R_{0}^2} [/math] [math]\lt =\gt [/math] [math] m_{0} \omega^2 R_{0} =\ G\frac{m_{0}M}{R_{0}^2} [/math] [math]\lt =\gt [/math] [math] \omega =\sqrt{\frac{GM}{R_{0}^3}}[/math].

Если учитывать, что угловая скорость твердотельного вращения без центрального тела имеет вид

[math] \omega_{s0} =\sqrt{\frac{3 \pi GNm_{0}}{4R_{0}^3}}[/math], где [math]N[/math] — число частиц

то получим, что искомая уловая скорость твердотельного вращения будет иметь вид

[math] \omega_{s} =\sqrt{\frac{3 \pi GNm_{0}}{4R_{0}^3}} + \sqrt{\frac{GM}{R_{0}^3}}[/math]

Задав отношение [math]\frac{\omega_{0}}{\omega_{s}}[/math], получаем значение угловой скорости облака [math]\omega_{0}[/math] Это отношение угловых скоростей позволяет сохранить подобие при изменении числа частиц.

Зная [math]\omega_{0}[/math] можно найти скорость частицы [math]V_{0} = [\omega,r][/math],где [math]r[/math] — расстояние до центра.

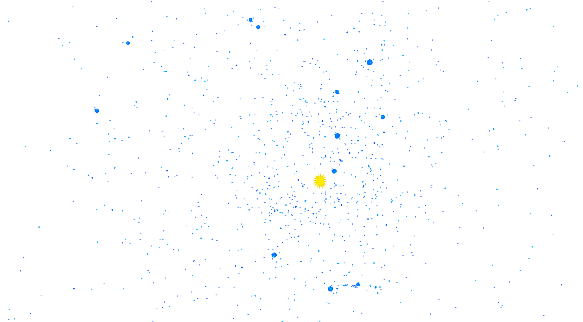
Результат работы программы при: [math]\frac{\omega_{0}}{\omega_{s}}[/math] = 1.05, [math]N[/math] = 10000

Видим 12 кластеров, движущиеся по орбитам. Этот результат получен после 24804 итераций. То есть при данном отношении угловых скоростей облако устойчиво.

Обсуждение результатов и выводы[править]

Полученные результаты позволяют исследовать зависимость поведения облака от параметров. Попытки привести значения переменных к значению констант системы Земля-Луна-Солнца оказались не плодотворными. Таким образом, для дальнейшего продвижения, необходимо далее исследовать влияние параметром на образование двойной системы. Помимо параметров динамических, необходимо рассматривать влияние и параметров геометрических, после чего уже можно будет пытаться применить к модели реальные параметры. После применения реальных параметров полученные результаты можно будет сравнить с теоретическими предсказаниями[2]

Ссылки по теме[править]

Земля-Луна

Интересные страницы по теме[править]

Кольца Сатурна

Система Земля - Луна

О разных гипотезах возникновения Луны

См. также[править]

• Справочная информация
• Курсовые проекты 2012
• Курсовые проекты 2013