MPI-программы — различия между версиями
(Новая страница: «== Блочная сортировка == http://ru.wikipedia.org/wiki/Блочная_сортировка Подробное описание метода Эт...») |
|||
| (не показаны 3 промежуточные версии 1 участника) | |||
| Строка 1: | Строка 1: | ||
== Блочная сортировка == | == Блочная сортировка == | ||
| − | + | [http://ru.wikipedia.org/wiki/Блочная_сортировка Подробное описание метода][[Файл: Sort.jpg|thumb|right]] | |
Это алгоритм сортировки, в котором сортируемые элементы распределяются между конечным числом отдельных блоков (карманов, корзин) так, чтобы все элементы в каждом следующем по порядку блоке были всегда больше (или меньше), чем в предыдущем. Каждый блок затем сортируется отдельно, либо рекурсивно тем же методом, либо другим. Затем элементы помещаются обратно в массив. Этот тип сортировки может обладать линейным временем исполнения. | Это алгоритм сортировки, в котором сортируемые элементы распределяются между конечным числом отдельных блоков (карманов, корзин) так, чтобы все элементы в каждом следующем по порядку блоке были всегда больше (или меньше), чем в предыдущем. Каждый блок затем сортируется отдельно, либо рекурсивно тем же методом, либо другим. Затем элементы помещаются обратно в массив. Этот тип сортировки может обладать линейным временем исполнения. | ||
При реализации алгоритма сортировки внутри блока использовался метод пузырька. Сортировку каждого блока осуществлял отдельный процессор. | При реализации алгоритма сортировки внутри блока использовался метод пузырька. Сортировку каждого блока осуществлял отдельный процессор. | ||
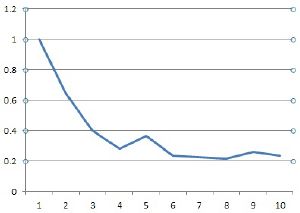
На рис. представлена зависимость относительного времени выполнения от числа процессоров для 10000 элементов. | На рис. представлена зависимость относительного времени выполнения от числа процессоров для 10000 элементов. | ||
| − | + | ||
| + | |||
== Метод Гаусса == | == Метод Гаусса == | ||
| − | + | [http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4_%D0%93%D0%B0%D1%83%D1%81%D1%81%D0%B0 Подробное описание метода] | |
| + | [[Файл: Gauss.jpg|thumb|right]] | ||
Классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. | Классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. | ||
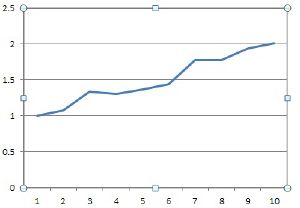
При реализации строки между процессорами распределялись таким образом, что процессор с номером i выполнял строки последовательно с промежутком, равным общему количеству процессоров. На рис. представлена зависимость относительного времени выполнения от числа процессоров для матрицы размером 1000 на 1000. | При реализации строки между процессорами распределялись таким образом, что процессор с номером i выполнял строки последовательно с промежутком, равным общему количеству процессоров. На рис. представлена зависимость относительного времени выполнения от числа процессоров для матрицы размером 1000 на 1000. | ||
| − | |||
Текущая версия на 15:52, 26 декабря 2012
Блочная сортировка[править]
Подробное описание методаЭто алгоритм сортировки, в котором сортируемые элементы распределяются между конечным числом отдельных блоков (карманов, корзин) так, чтобы все элементы в каждом следующем по порядку блоке были всегда больше (или меньше), чем в предыдущем. Каждый блок затем сортируется отдельно, либо рекурсивно тем же методом, либо другим. Затем элементы помещаются обратно в массив. Этот тип сортировки может обладать линейным временем исполнения. При реализации алгоритма сортировки внутри блока использовался метод пузырька. Сортировку каждого блока осуществлял отдельный процессор. На рис. представлена зависимость относительного времени выполнения от числа процессоров для 10000 элементов.
Метод Гаусса[править]
Классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. При реализации строки между процессорами распределялись таким образом, что процессор с номером i выполнял строки последовательно с промежутком, равным общему количеству процессоров. На рис. представлена зависимость относительного времени выполнения от числа процессоров для матрицы размером 1000 на 1000.