Неполнота Ньютона и нецентральное взаимодействие — различия между версиями
Hofa (обсуждение | вклад) (Новая страница: «Комментарий к параграфу 8.4 «Иллюстрация неполноты механики Ньютона», на стр.255 книги П.А. Ж...») |
Hofa (обсуждение | вклад) |
||
| (не показано 6 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | Комментарий к параграфу 8.4 | + | Комментарий к параграфу 8.4 «'''Иллюстрация неполноты механики Ньютона'''», на стр.255 книги П.А. Жилина |
«Теоретическая механика. Фундаментальные законы механики» | «Теоретическая механика. Фундаментальные законы механики» | ||
| − | '''П.А.Жилин:'' | + | '''П.А.Жилин:''' |
| + | |||
Построение определяющих уравнений относится к числу трудных проблем механики. Часто поступают так. На основе интуитивных соображений задаются какими-то определяющими уравнениями и, тем самым, получают замкнутую систему уравнений, описывающую механическое поведение рассматриваемой умозрительной системы. Исследуют поведение этой системы. Если оказывается, что поведение умозрительной системы в основных чертах совпадает с наблюдаемым поведением реальной системы, то определяющие уравнения считаются приемлемыми. Если этого нет, то ищут другие определяющие уравнения. | Построение определяющих уравнений относится к числу трудных проблем механики. Часто поступают так. На основе интуитивных соображений задаются какими-то определяющими уравнениями и, тем самым, получают замкнутую систему уравнений, описывающую механическое поведение рассматриваемой умозрительной системы. Исследуют поведение этой системы. Если оказывается, что поведение умозрительной системы в основных чертах совпадает с наблюдаемым поведением реальной системы, то определяющие уравнения считаются приемлемыми. Если этого нет, то ищут другие определяющие уравнения. | ||
На примере маятника демонстрируется неполнота центрального взаимодействия Ньютона. | На примере маятника демонстрируется неполнота центрального взаимодействия Ньютона. | ||
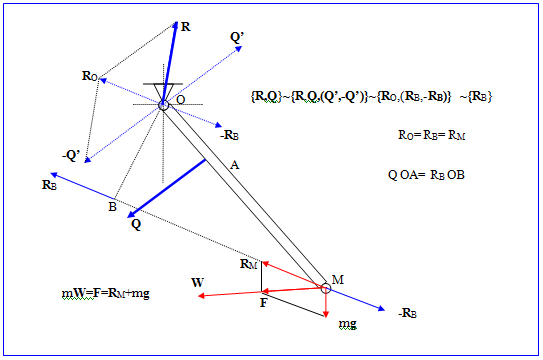
Однако не учитывается, что невесомый стержень способен действовать на массу маятника в любом направлении, а не только вдоль стержня. Рисунок демонстрирует, как это происходит. | Однако не учитывается, что невесомый стержень способен действовать на массу маятника в любом направлении, а не только вдоль стержня. Рисунок демонстрирует, как это происходит. | ||
| + | |||
| + | [[Файл:pend.png|thumb|center|900px|Математический маятник]] | ||
| + | |||
| + | # Cилы, приложенные к твердому телу без массы (пустое тело) всегда находятся в равновесии, т.е сводимы к двум силам одинакового модуля с общей линией действия и противоположными направлениями и двум вращательным системам с одинаковыми по модулю и противоположными по направлению моментами. | ||
| + | # В данном случае, кода тело передает усилия материальной точке, моменты отсутствуют. Реакция '''R''' шарнира О и сила '''Q''' со стороны пружины эквивалентны силе '''R'''B ('''R'''M), которая и действует на материальную точку М | ||
| + | |||
| + | Свойство пустого тела передавать усилия не точке, а телу, можно продемонстрировать на сковороде. Ручка сковороды (пустое тело) нагружена тремя уравновешенными моментами, а сама сковорода – двумя. Если сковороду подвесить за ручку и поставить спиральную пружину, то получим физический маятник, в котором пустая ручка передает силы и моменты аналогично тому как это происходит в математическом маятнике. Таким образом, нецентральное взаимодествие возможно только при наличии передающего пустого тела. | ||
| + | |||
| + | [[Файл:pan.png|thumb|center|400px|Сковорода]] | ||
| + | |||
| + | == См. также== | ||
| + | [[Работы Костарева А.В]] | ||
Текущая версия на 21:57, 8 декабря 2014
Комментарий к параграфу 8.4 «Иллюстрация неполноты механики Ньютона», на стр.255 книги П.А. Жилина «Теоретическая механика. Фундаментальные законы механики»
П.А.Жилин:
Построение определяющих уравнений относится к числу трудных проблем механики. Часто поступают так. На основе интуитивных соображений задаются какими-то определяющими уравнениями и, тем самым, получают замкнутую систему уравнений, описывающую механическое поведение рассматриваемой умозрительной системы. Исследуют поведение этой системы. Если оказывается, что поведение умозрительной системы в основных чертах совпадает с наблюдаемым поведением реальной системы, то определяющие уравнения считаются приемлемыми. Если этого нет, то ищут другие определяющие уравнения.
На примере маятника демонстрируется неполнота центрального взаимодействия Ньютона. Однако не учитывается, что невесомый стержень способен действовать на массу маятника в любом направлении, а не только вдоль стержня. Рисунок демонстрирует, как это происходит.
- Cилы, приложенные к твердому телу без массы (пустое тело) всегда находятся в равновесии, т.е сводимы к двум силам одинакового модуля с общей линией действия и противоположными направлениями и двум вращательным системам с одинаковыми по модулю и противоположными по направлению моментами.
- В данном случае, кода тело передает усилия материальной точке, моменты отсутствуют. Реакция R шарнира О и сила Q со стороны пружины эквивалентны силе RB (RM), которая и действует на материальную точку М
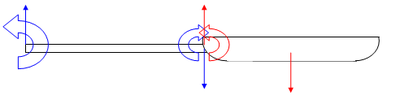
Свойство пустого тела передавать усилия не точке, а телу, можно продемонстрировать на сковороде. Ручка сковороды (пустое тело) нагружена тремя уравновешенными моментами, а сама сковорода – двумя. Если сковороду подвесить за ручку и поставить спиральную пружину, то получим физический маятник, в котором пустая ручка передает силы и моменты аналогично тому как это происходит в математическом маятнике. Таким образом, нецентральное взаимодествие возможно только при наличии передающего пустого тела.