Устинова Алеся: Определение временных характеристик разрушения — различия между версиями
Алеся (обсуждение | вклад) (→Контакт Герца) |
Алеся (обсуждение | вклад) (→Ссылки) |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 85: | Строка 85: | ||
<math> | <math> | ||
| − | U_z=\frac{1}{\pi E^*}\ | + | U_z=\frac{1}{\pi E^*}\iint p(x',y')\frac{dx'dy'}{r} |
</math> | </math> | ||
<math> | <math> | ||
| Строка 153: | Строка 153: | ||
<math> | <math> | ||
F=\frac{4}{3} E^* R^{1/2} d^{3/2} | F=\frac{4}{3} E^* R^{1/2} d^{3/2} | ||
| + | </math> | ||
| + | |||
| + | ==Контакт между двух упругих тел с изогнутыми поверхностями== | ||
| + | [[Файл: R3.PNG|340px|thumb|right|Рисунок 3. Контакт между двумя телами с изогнутыми поверхностями]] | ||
| + | Оба тела упруги, поэтому воспользуемся следующим выражением <math>E^*</math> | ||
| + | |||
| + | <math> | ||
| + | \frac{1}{E*}=\frac{1- \nu_1^2}{E_1}+\frac{1- \nu_2^2}{E_2} | ||
| + | </math> | ||
| + | |||
| + | <math>E_1</math> и <math>E_2</math> - модуль упругости, <math>\nu_1</math> и <math>\nu_2</math> - коэффициент Пуассона | ||
| + | |||
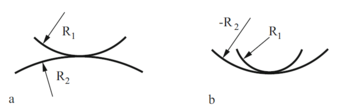
| + | Если у двух сфер с радиусами <math>R_1</math> и <math>R_2</math> в контакте (рисунок 3), то уравнения (см. выше) по-прежнему в соответствии с радиусом R | ||
| + | |||
| + | <math> | ||
| + | \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2} | ||
</math> | </math> | ||
| Строка 198: | Строка 214: | ||
[http://www.krugosvet.ru/enc/nauka_i_tehnika/tehnologiya_i_promyshlennost/METALLOV_ISPITANIYA.html Испытания металлов] | [http://www.krugosvet.ru/enc/nauka_i_tehnika/tehnologiya_i_promyshlennost/METALLOV_ISPITANIYA.html Испытания металлов] | ||
| + | |||
| + | [http://en.wikipedia.org/wiki/Help:Displaying_a_formula Тех] | ||
== См. также == | == См. также == | ||
* [[Устинова Алеся]] | * [[Устинова Алеся]] | ||
Текущая версия на 01:09, 12 июля 2012
Содержание
Введение[править]
Процесс разрушения представляет собой сложный многоступенчатый временной процесс, начинающийся задолго до появления видимых трещин и заканчивающийся прорастанием трещины и разделением тела на части.
Закономерности процесса разрушения изучаются на различных масштабных уровнях с помощью тончайших физических экспериментов. На каждом масштабном уровне (от атомно-молекулярного до макроразмеров порядка километров) предлагаются определённые физические модели процесса разрушения, учитывающие параметры структуры и условия перехода разрушения с одного масштабного уровня на другой.
Согласно энергетической модели разрушения, практически использованной Гриффитсом А.А. в 1920 г., условием развития трещины является подвод энергии к её вершине. При разрушении находящегося под напряжением элементарного кубика с ребром длиною R освобождается энергия его упругого деформирования
где
- сила упругого деформирования кубика, Е - модуль упругости материала, - абсолютное удлинение одной из сторон кубика при его одноосном растяжении.
Приращение длины разрыва (трещины) на величину dR приведёт к высвобождению дополнительного количества энергии упругого деформирования, равного σ 2 R 2 dR / 2E. С другой стороны, образование разрыва приводит к увеличению площади поверхности и поверхностной энергии тела на величину γ R dR (γ - удельная работа разрушения на единицу площади новой поверхности). Рассмотрев условия энергетического баланса и приравняв оба этих значения, получим формулу Гриффитса для разрушающих напряжений тела с трещиной и критического размера Rкр трещины, после достижения которого начинается самопроизвольный её рост в поле создаваемых ею перенапряжений
σ ~ √ 2 γ E / R
Rкр ~ 2 γ E / σ 2
Несколько иная (силовая) модель разрушения была предложена Ирвином, в которой критерием роста трещины был принят момент достижения критического значения коэффициентом интенсивности напряжений К, являющимся функцией только характера внешнего нагружения, геометрии тела и размеров трещины. Согласно предложению Ирвина, трещина не развивается, когда значения К не превышают некоторой критической. Интенсивность напряжений - это некоторая фиктивная величина, связанная с главными напряжениями и используемая для оценки сложного напряжённого состояния.
Деформация упругого полупространства под действие поверхностных сил[править]
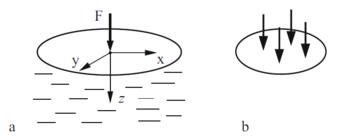
Рассмотрим упругую среду (см. рис. 1).
Сдвиги, вызванные силой:
где
.
Смещение свободной поверхности z=0
, , ,
где
.
в случае непрерывного распределения P (х,у) нормального давления, смещение поверхности
где
Предположим, что в круговой области радиуса, распределение давления
Распределение давления Герца (n=1/2)
приводит к вертикальному перемещению
Полная сила
Контакт Герца[править]
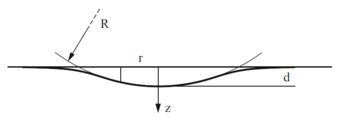
На рисунке 2 схематически показан контакт между жесткой сферой и упругим полупространством. Смещение точек поверхности и площадь контакта между первоначально плоской поверхностью и жесткой сферой радиусом R равна
Уравнение вертикальных перемещений, является квадратичным распределением вертикальных смещений по распределению давления в форме.
Подберем параметры и , так что распределение давления точного перемещения, вызванные:
и должны отвечать следующим требованиям
контакт с радиусом
максимальное давление
получаем Нормальная сила
Контакт между двух упругих тел с изогнутыми поверхностями[править]
Оба тела упруги, поэтому воспользуемся следующим выражением
и - модуль упругости, и - коэффициент Пуассона
Если у двух сфер с радиусами и в контакте (рисунок 3), то уравнения (см. выше) по-прежнему в соответствии с радиусом R
Нормальная сила:
Сила адгезии:
A - площадь круга
h - 1/2 хорды