Нейронные сети - теория и приложения. — различия между версиями
(Новая страница: «===Искуственные нейронные сети=== Нейронная сеть это вычислительная модель, созданная на ос...») |
|||
| (не показано 7 промежуточных версий этого же участника) | |||
| Строка 29: | Строка 29: | ||
==Обучение== | ==Обучение== | ||
| − | Для обучения применяется алгоритм обратного распространения ошибки. У сети есть множество входов <math>x_1, ..., x_n</math>, Обозначим через <math>w_{i,j}</math> вес, стоящий на ребре, соединяющем i-й и j-й узлы, а через <math>o_i</math> — выход i-го узла. Если нам известен обучающий пример (правильные ответы сети <math>t_k | + | Для обучения применяется алгоритм обратного распространения ошибки. У сети есть множество входов <math>x_1, ..., x_n</math>, Обозначим через <math>w_{i,j}</math> вес, стоящий на ребре, соединяющем i-й и j-й узлы, а через <math>o_i</math> — выход i-го узла. Если нам известен обучающий пример (правильные ответы сети <math>t_k</math>), то функция ошибки, полученная по методу наименьших квадратов, выглядит так: |
| − | + | <math>E(\{w_{i,j}\}) =\cfrac{1}{2} \sum_{k} (t_k - o_k)^2 </math> | |
На каждом шаге будем добавлять к весу. | На каждом шаге будем добавлять к весу. | ||
| Строка 49: | Строка 49: | ||
#: Для всех d от 1 до m: | #: Для всех d от 1 до m: | ||
## Подать <math>\{x_i^d\}</math> на вход сети и подсчитать выходы <math>o_i</math> каждого узла. | ## Подать <math>\{x_i^d\}</math> на вход сети и подсчитать выходы <math>o_i</math> каждого узла. | ||
| − | ## Для всех <math>k | + | ## Для всех <math>k </math> |
##: <math>\delta _k = o_k(1 - o_k)(t_k - o_k)</math>. | ##: <math>\delta _k = o_k(1 - o_k)(t_k - o_k)</math>. | ||
## Для каждого уровня l, начиная с предпоследнего: | ## Для каждого уровня l, начиная с предпоследнего: | ||
| Строка 60: | Строка 60: | ||
где <math>\alpha</math> - коэффициент инерциальнности для сглаживания резких скачков при перемещении по поверхности целевой функции | где <math>\alpha</math> - коэффициент инерциальнности для сглаживания резких скачков при перемещении по поверхности целевой функции | ||
| + | |||
| + | ==Использование== | ||
| + | |||
| + | На практике, удобнее разрабатывать алгоритмы в пакете Matlab, где для работы с нейронным сетями есть Neural Network Toolbox. Его средствами можно построить сеть и обучить ее на наборе данных. | ||
| + | Для удобства пользователя предусмотрен GUI который запускается командой >>nnstart | ||
| + | |||
| + | Кроме того, можно использовать инструменты NNToolbox прямо в коде | ||
| + | |||
| + | Попробуем решить простейшую задачу экстраполяции на примере параболы. | ||
| + | |||
| + | |||
| + | |||
| + | for i=1:6 | ||
| + | Набор данных для обучения | ||
| + | inputs = [1:10]; | ||
| + | targets =inputs.*inputs; | ||
| + | Создание сети с i*2 нейронами | ||
| + | hiddenLayerSize = i*2; | ||
| + | net = fitnet(hiddenLayerSize); | ||
| + | subplot(2,3,i) | ||
| + | plot(inputs,targets,'r') | ||
| + | hold on | ||
| + | Разделение данных на набор для обучения,валидации и тестирования | ||
| + | net.divideParam.trainRatio = 80/100; | ||
| + | net.divideParam.valRatio = 20/100; | ||
| + | net.divideParam.testRatio = 0/100; | ||
| + | Обучение | ||
| + | [net,tr] = train(net,inputs,targets); | ||
| + | Тестирование | ||
| + | inputs=[1:0.1:20] | ||
| + | outputs = net(inputs); | ||
| + | plot(inputs,outputs) | ||
| + | end | ||
| + | |||
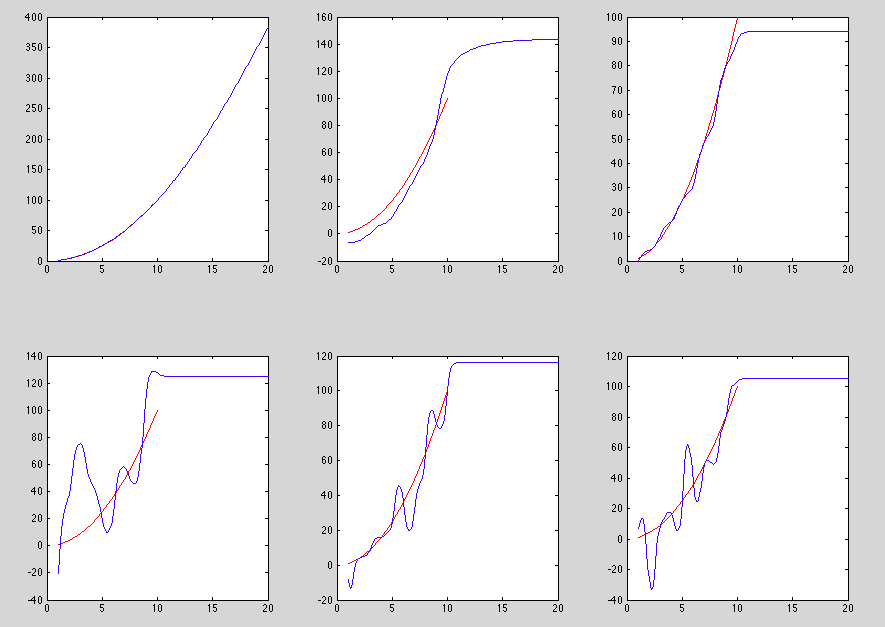
| + | Результат для 2,4,6,8,10,12 нейронных сетей. Красная линия - тренировочный набор. Синяя - результат работы сети. | ||
| + | |||
| + | [[Файл:graph12345.png]] | ||
Текущая версия на 16:17, 24 мая 2012
Содержание
Искуственные нейронные сети[править]
Нейронная сеть это вычислительная модель, созданная на основании исследований работы нервной системы человека как попытка создания искуственного интелекта. Разумеется это лишь упрощенная модель, которая не отражает всей сложности процессов происходящих в мозгу человека, однако она нашла применение в областях, где традиционные методы расчета не применимы.В основном это решение задач, сформулировать которые математически крайне сложно, а зачастую и невозможно. Искуственные нейронные сети применяются для:
- Распознование образов
Символов,звуков,анализ изображений. Сеть обучается набором известных образов, а затем может самостоятельно классифицировать до этого не известные ей образы.
- Управление
Создание так называемых мастер-систем, способных принимать решение подобно человеку, управлять техникой даже в случае поломок. Мастер-системы характеризуются значительной адаптивностью. Как правило на вход подаются данные о состоянии системы (Например ориентация самолета в пространстве, его скорости,параметры среды и желаемое направление полета),а на выходе сеть сообщает управление,которое необходимо применить к систем, с целью минимизации функции оценки(например расхождение текущего курса с желаемым).
- Составление прогнозов
Например на котировки акций, сеть обучается по архивам биржи,а затем строит предположение о развитии ситуации на рынке.
- Ассоциативная память
Сети способны запоминать информацию подобно человеческому мозгу, что способствует эффективному сжатию
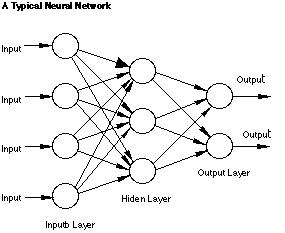
Структура сети[править]
Сеть состоит из элементов называемых нейронами, соединенных связями, причем каждая связь характеризуется весом. Вес - это коэффициент на который умножается сигнал при прохождении через связь. Нейроны объединяются в слои, нейронная сеть обязательно имеет входной и выходной слои. Количество внутренних или скрытых слоев может быть произвольным, однако по мере увеличения их количества усиливается память сети, что негативно влияет на обучение. Поэтому обычно используются сети с меньшим количеством слоев, но с большим количеством нейронов в каждом.
Активация нейронов[править]
Каждый нейрон представляет из себя некоторую функцию,ее называют функцией активации. В зависимости от предназначения сети испольуются различные типы :
- Бинарные
В зависимости от значения поступившего на вход, нейрон возвращает либо 0 либо 1. Чаще всего используется Функция Хевисайда
- Линейные
- Нелинейные
Нелинейные функции акивации позволяют добиваться результатов меньшим числом нейронов. Наиболее используемой является сигмоидная функция.
Обучение[править]
Для обучения применяется алгоритм обратного распространения ошибки. У сети есть множество входов , Обозначим через вес, стоящий на ребре, соединяющем i-й и j-й узлы, а через — выход i-го узла. Если нам известен обучающий пример (правильные ответы сети ), то функция ошибки, полученная по методу наименьших квадратов, выглядит так:
На каждом шаге будем добавлять к весу.
- ,
где -- множитель, задающий скорость "движения".
Алгоритм[править]
При программировании алгоритм выглядит следующим образом:
- Для всех d от 1 до m:
- Подать на вход сети и подсчитать выходы каждого узла.
- Для всех
- .
- Для каждого уровня l, начиная с предпоследнего:
- Для каждого узла j уровня l вычислить
- .
- Для каждого ребра сети {i, j}
- .
- .
- Выдать значения .
где - коэффициент инерциальнности для сглаживания резких скачков при перемещении по поверхности целевой функции
Использование[править]
На практике, удобнее разрабатывать алгоритмы в пакете Matlab, где для работы с нейронным сетями есть Neural Network Toolbox. Его средствами можно построить сеть и обучить ее на наборе данных. Для удобства пользователя предусмотрен GUI который запускается командой >>nnstart
Кроме того, можно использовать инструменты NNToolbox прямо в коде
Попробуем решить простейшую задачу экстраполяции на примере параболы.
for i=1:6 Набор данных для обучения inputs = [1:10]; targets =inputs.*inputs; Создание сети с i*2 нейронами hiddenLayerSize = i*2; net = fitnet(hiddenLayerSize); subplot(2,3,i) plot(inputs,targets,'r') hold on Разделение данных на набор для обучения,валидации и тестирования net.divideParam.trainRatio = 80/100; net.divideParam.valRatio = 20/100; net.divideParam.testRatio = 0/100; Обучение [net,tr] = train(net,inputs,targets); Тестирование inputs=[1:0.1:20] outputs = net(inputs); plot(inputs,outputs) end
Результат для 2,4,6,8,10,12 нейронных сетей. Красная линия - тренировочный набор. Синяя - результат работы сети.