Моделирование гидроразрыва пласта — различия между версиями
Kuzkin (обсуждение | вклад) м |
(новый источник) |
||
| (не показано 58 промежуточных версий 7 участников) | |||
| Строка 1: | Строка 1: | ||
| + | [[Кафедра "Теоретическая механика"]] > '''Моделирование гидроразрыва пласта''' <HR> | ||
| + | |||
| + | {{DISPLAYTITLE:<span style="display:none">{{FULLPAGENAME}}</span>}} | ||
| + | <font size="5">Моделирование гидроразрыва пласта </font> | ||
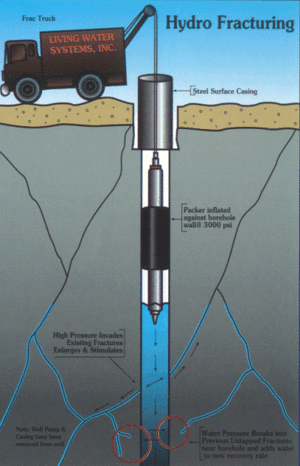
[[Файл:Hydro-fracture.gif|thumb|300px|right|[http://www.davidicke.com/articles/corporate-crime/43173-oil-and-gas-collection-hydraulic-fracturing-toxic-chemicals-and-the-surge-of-earthquake-activity-in-arkansas Схема гидроразрыва]]] | [[Файл:Hydro-fracture.gif|thumb|300px|right|[http://www.davidicke.com/articles/corporate-crime/43173-oil-and-gas-collection-hydraulic-fracturing-toxic-chemicals-and-the-surge-of-earthquake-activity-in-arkansas Схема гидроразрыва]]] | ||
| Строка 14: | Строка 18: | ||
Особенности "реального" процесса гидроразрыва: | Особенности "реального" процесса гидроразрыва: | ||
* неоднорподность (в частности, слоистая структура) горной породы; | * неоднорподность (в частности, слоистая структура) горной породы; | ||
| − | * changes in magnitude and/or orientation of the in situ confining stresses; | + | * изменения в величине и/или ориентации сжимающих пластовых напряжений (changes in magnitude and/or orientation of the in situ confining stresses); |
| − | * | + | * присутствие свободных порехностей; |
* утечка жидкости, используемой для гидроразрыва, в горную породу либо наоборот приток жидкости в трещины из породы; | * утечка жидкости, используемой для гидроразрыва, в горную породу либо наоборот приток жидкости в трещины из породы; | ||
* влияние температуры и сдвига на реологические свойства разрушающей жидкости; | * влияние температуры и сдвига на реологические свойства разрушающей жидкости; | ||
* закрытие трещин в следствие прекращения накачки жидкости, намеренной откачки жидкости или резкого изменения геометрии за счет образования трещин (разгрузка породы); | * закрытие трещин в следствие прекращения накачки жидкости, намеренной откачки жидкости или резкого изменения геометрии за счет образования трещин (разгрузка породы); | ||
| − | * '''гидроразрыв так называемых ‘‘мягких’’ пород, таких как слабо | + | * '''гидроразрыв так называемых ‘‘мягких’’ пород, таких как слабо консолидированный песчанник (weakly consolidated sandstone). |
| + | |||
| + | == Проблемы и задачи, возникающие при использовании технологии гидроразрыва == | ||
| + | |||
| + | * prediction of fracture geometry (предсказание геометрии трещины, т.е. её полудлины, высоты и ширины раскрытия) | ||
| + | * effective prevention of crack closure (выбор оптимальных свойств проппанта (размеров, плотности, механических свойств, проницаемости упаковки), а также технологии его введения в трещину гидроразрыва) | ||
| + | * optimal choice of fracturing fluid (жидкость должна обеспечивать эффективный транспорт проппанта, а частности, иметь достаточную вязкость. Кроме того, должна обеспечиваться быстрая откачка жидкости после завершения технологического процесса) | ||
| + | * fluid leak-off (утечка жидкости для гидроразрыва из скважины в прилегающую породу) | ||
| + | * avoid screenouts caused by proppant a bridging and holdup (частицы проппанта могут застревать в трещинах, образуя мостики, препятствующие течению жидкости, используемой для гидроразрыва, и/или добывемого флюида (нефти, газа и т.д.). В результате может существенно снижаться продуктивность скважины) | ||
| + | * proppant flowback (при прекращении закачки жидкости в скважину может происходить движение проппанта в обратном направлении) | ||
| − | == | + | == Модели, используемые в литературе == |
Для моделирования разрушения горной породы в процессе гидроразрыва используются как методы механики сплошной среды (ассимптотические методы, метод конечных элементов, метод граничных элементов), так и механики дискретных сред (метод дискретных элементов). | Для моделирования разрушения горной породы в процессе гидроразрыва используются как методы механики сплошной среды (ассимптотические методы, метод конечных элементов, метод граничных элементов), так и механики дискретных сред (метод дискретных элементов). | ||
=== Континуальные подходы к моделированию гидроразрыва === | === Континуальные подходы к моделированию гидроразрыва === | ||
| − | * '''Adachia J., Siebritsb E., Peircec A., Desroches J. Computer simulation of hydraulic fractures // Int. J. of Rock Mechanics & Mining Sciences, 44, 2007, pp. 739–757''' | + | Основные континуальные модели, используемые в литературе для моделирования гидроразрыва: |
| − | В статье дается обзор континуальных подходов к моделированию гидроразрыва. В частности, отмечается, что при использовании континуальных методов, как правило, вводятся следующие ограничения: | + | |
| + | '''2D Models''' | ||
| + | * Perkins‐Kern Nordgren (PKN) | ||
| + | * Khristianovich‐Geertsma‐DeKlerk (KGD) | ||
| + | * Penny‐Frac | ||
| + | * [http://www.geo.umass.edu/faculty/cooke/fric2d/chapter1.html Displacement Discontinuity Model] | ||
| + | |||
| + | '''Lumped Parameter Models''' | ||
| + | * [http://www.carboceramics.com/fracpropt-software/ FracPro] | ||
| + | * FracPro‐PT | ||
| + | |||
| + | '''Pseudo‐3D Models''' | ||
| + | * [http://www.mfrac.com/ MFRAC] | ||
| + | * [http://www.nsitech.com/index.php/stimplan-software.html StimPlan], e‐StimPlan | ||
| + | * FracCade | ||
| + | |||
| + | '''3D Models''' | ||
| + | * [http://www.gohfer.com/ GOHFER] | ||
| + | * [http://www.nsitech.com/index.php/stimplan-software.html N‐StimPlan] | ||
| + | * Terra‐Frac | ||
| + | |||
| + | Некоторые статьи по гидроразрыву. | ||
| + | |||
| + | * '''Adachia J., Siebritsb E., Peircec A., Desroches J. Computer simulation of hydraulic fractures // Int. J. of Rock Mechanics & Mining Sciences, 44, 2007, pp. 739–757 ([[Медиа: Adachi_SimulHydrFrac.pdf |download, pdf]])'''. В статье дается обзор континуальных подходов к моделированию гидроразрыва. В частности, отмечается, что при использовании континуальных методов, как правило, вводятся следующие ограничения: | ||
** материал резервуара (горной породы) считается линейно упругим; | ** материал резервуара (горной породы) считается линейно упругим; | ||
** в случае слоистого резервуара слои считаются параллельными и идеально сопряженными; | ** в случае слоистого резервуара слои считаются параллельными и идеально сопряженными; | ||
| − | ** гидроразрыв происходит в одной вертикальной | + | ** гидроразрыв происходит в одной вертикальной плоскости; |
** принимается модель Ньютоновской жидкости или жидкости с степенным учавнением состояния; | ** принимается модель Ньютоновской жидкости или жидкости с степенным учавнением состояния; | ||
| Строка 41: | Строка 77: | ||
** влияние утечки жидкости на давление внутри трещин. | ** влияние утечки жидкости на давление внутри трещин. | ||
| − | |||
| − | |||
| − | |||
| − | * ''' | + | * '''Olson J.E. Multi-fracture propagation modeling: Applications to hydraulic fracturing in shales and tight gas sands // 42nd US Rock Mechanics Symposium, 2008'''. The diagnostic data suggests that in some situations, complex, multistranded fracture zones or networks develop as a result of interaction between the hydraulic fracture and pre-existing natural fractures. This paper examines complex hydraulic fracture pattern development using techniques previously applied to the analysis of natural fracture network development and the fracture of silicon wafers in microchip manufacture. The numerical code is based on a pseudo-3d displacement discontinuity solution, where the propagation of hundreds of fracture tips can be tracked simultaneously, with propagation velocities proportional to the stress intensity factor at each crack tip. The method does not yet solve for flow through the hydraulic fracture network, but instead uses a simplified constant pressure boundary condition for all fracture segments connected to the wellbore, enabling a preliminary analysis of this complex problem. |
| − | The | + | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | * '''Lin J., Zhu D. Predicting well performance in complex fracture systems by slab source method // SPE Hydraulic fracturing conference, 2012.''' The model for the flow inside fracture pattern is proposed. | ||
| + | |||
| + | |||
| + | *'''Fu P., Johnson S.M., Hao Y., Carrigan C.R. Fully coupled geomechanics and discrete flow network modeling of hydraulic fracturing for geothermal applications // Proc. of 36 Workshop on Geothermal Reservoir Engineering'''. The primary objective of our current research is to develop a computational test bed for evaluating borehole techniques to enhance fluid flow and heat transfer in enhanced geothermal systems (EGS). Simulating processes resulting in hydraulic fracturing and/or the remobilization of existing fractures, especially the interaction between propagating fractures and existing fractures, represents a critical goal of our project. To this end, we are continuing to develop a hydraulic fracturing simulation capability within the Livermore Distinct Element Code (LDEC), a combined FEM/DEM analysis code with explicit solid-fluid mechanics coupling. LDEC simulations start from an initial fracture distribution which can be stochastically generated or upscaled from the statistics of an actual fracture distribution. During the hydraulic stimulation process, LDEC tracks the propagation of fractures and other modifications to the fracture system. The output is transferred to the Non-isothermal Unsaturated Flow and Transport (NUFT) code to capture heat transfer and flow at the reservoir scale. | ||
=== Дискретные подходы к моделированию гидроразрыва === | === Дискретные подходы к моделированию гидроразрыва === | ||
| Строка 57: | Строка 90: | ||
Для дискретного моделирования процесса гидроразрыва в литературе, как правило, применяется метод дискретных элементов (DEM). При этом горная порода представляется в виде "связанных" (bonded) частиц, как правило, сферической формы. Для описания взаимодействий между частицами (связей) используется модель [[BPM | Bonded Particle Model (BPM)]], реже модель упругого стержня, соединяющего центры частиц. Для описания течения жидкости в трещинах гидроразрыва применяется модель, изложенная в '''Shimizu Y. Fixed coarse-grid fluid scheme in PFC2D, Itasca Consulting Group, Inc., Minnesota, 2008'''. | Для дискретного моделирования процесса гидроразрыва в литературе, как правило, применяется метод дискретных элементов (DEM). При этом горная порода представляется в виде "связанных" (bonded) частиц, как правило, сферической формы. Для описания взаимодействий между частицами (связей) используется модель [[BPM | Bonded Particle Model (BPM)]], реже модель упругого стержня, соединяющего центры частиц. Для описания течения жидкости в трещинах гидроразрыва применяется модель, изложенная в '''Shimizu Y. Fixed coarse-grid fluid scheme in PFC2D, Itasca Consulting Group, Inc., Minnesota, 2008'''. | ||
| − | |||
Приведем выдержки из некоторых статей по дискретному моделирвоанию гидроразрыва. | Приведем выдержки из некоторых статей по дискретному моделирвоанию гидроразрыва. | ||
| + | * '''Torres S.A.G., Castaño J.D.M. Simulation of the hydraulic fracture process in two dimensions using a discrete element method// Phys. Rev. E 75, 066109, 2007'''. We introduce a discrete element simulation for the hydraulic fracture process in a petroleum well which takes into account the elastic behavior of the rock and the Mohr-Coulomb fracture criteria. The rock is modeled as an array of Voronoi polygons joined by elastic beams, which are submitted to tectonical stresses and the hydrostatic pressure of the fracturing fluid. The fluid pressure is treated like that of a hydraulic column. We also include an analysis of the fracturing fluid loss due to the permeability of the rock which is useful in an efficiency analysis of the treatment. | ||
| − | |||
| − | |||
* '''S. Deng, R. Podgorney, H. Huang, Discrete Element Modeling of rock deformation, fracture network development, permeability evolution under hydraulic stimulation // Proc. 36 Workshop on Geothermal reservoir engineering, 2011.''' | * '''S. Deng, R. Podgorney, H. Huang, Discrete Element Modeling of rock deformation, fracture network development, permeability evolution under hydraulic stimulation // Proc. 36 Workshop on Geothermal reservoir engineering, 2011.''' | ||
** 3D discrete element method with bonded particle model (BPM) | ** 3D discrete element method with bonded particle model (BPM) | ||
** two way coupling with fluid dynamics (model for network fluid flow) | ** two way coupling with fluid dynamics (model for network fluid flow) | ||
| + | |||
* '''J.P. Pruiksma, A. Bezuijen Hydraulic fracturing with distinct element method // Report of DELFRAC consortium, 2002'''. In this report, hydraulic fracturing is investigated using the distinct element code PFC2D from Itasca. Special routines adding fluid flow to PFC2D and updating the fluid flow domains when fractures appear. After the set-up of the hydraulic fracturing simulations has been discussed, with all the main input parameters, several main parameters are varied to study the resulting fracture patterns, pressure distributions and borehole pressures. These parameter studies are: particle size dependency of the simulations, behaviour at various confining stresses, the influence of the internal friction angle of the sand and the fracturing behaviour for different borehole injection rates. After this parameter study, comparisons are made with experiments done at TU Delft, GeoDelft and in the literature. The simulation results show the same trends as the experiments and are also in good agreement quantitatively (2D discrete element method with bonded particle model (BPM)) | * '''J.P. Pruiksma, A. Bezuijen Hydraulic fracturing with distinct element method // Report of DELFRAC consortium, 2002'''. In this report, hydraulic fracturing is investigated using the distinct element code PFC2D from Itasca. Special routines adding fluid flow to PFC2D and updating the fluid flow domains when fractures appear. After the set-up of the hydraulic fracturing simulations has been discussed, with all the main input parameters, several main parameters are varied to study the resulting fracture patterns, pressure distributions and borehole pressures. These parameter studies are: particle size dependency of the simulations, behaviour at various confining stresses, the influence of the internal friction angle of the sand and the fracturing behaviour for different borehole injection rates. After this parameter study, comparisons are made with experiments done at TU Delft, GeoDelft and in the literature. The simulation results show the same trends as the experiments and are also in good agreement quantitatively (2D discrete element method with bonded particle model (BPM)) | ||
| − | * '''H. Shimizu, T.Koyama, S. Murata, T. Ishida, M. Chijimatsu, T. Fujita, S. Nakama Distinct element modeling for Class II behavior of rock and hydraulic fracturing // International Journal of the JCRM vol.7, 2011, pp.33-36 | + | |
| + | * '''H. Shimizu, T.Koyama, S. Murata, T. Ishida, M. Chijimatsu, T. Fujita, S. Nakama Distinct element modeling for Class II behavior of rock and hydraulic fracturing // International Journal of the JCRM vol.7, 2011, pp.33-36'''. Newly developed numerical approaches using the Distinct Element Method (DEM) were presented, and a series of DEM simulations were performed for better understanding the physical phenomena and mechanism for the following two fundamental issues in rock engineering field. The first issue is the Class II behavior of the brittle rocks under uniaxial compression. The radial strain control method for uniaxial compression tests was introduced in the DEM codes and the Class II behavior of rocks was simulated. The simulation results suggest that the DEM can reproduce the Class II behavior of the rock successfully and revealed that the loading condition of rocks (radial strain control) will play an important role for the Class II behavior. The second issue is the hydraulic fracturing behavior in rocks. A series of simulations for hydraulic fracturing in rock was performed by using the flow-coupled DEM code. Simulation results clearly show that the fluid infiltration behavior depends on the fluid viscosity (2D discrete element method with bonded particle model (BPM)) | ||
| + | |||
*'''Park N. DE modeling of rock fracture behavior: fracture toughness and time-dependent fracture growth // PhD thesis, 2006.''' | *'''Park N. DE modeling of rock fracture behavior: fracture toughness and time-dependent fracture growth // PhD thesis, 2006.''' | ||
** 3D discrete element method with bonded particle model (BPM) | ** 3D discrete element method with bonded particle model (BPM) | ||
** Cundal's model for fluid flow is used (unpublished) | ** Cundal's model for fluid flow is used (unpublished) | ||
| + | |||
* '''Wu R. Some Fundamental Mechanisms of Hydraulic Fracturing, PhD thesis, 2006''' | * '''Wu R. Some Fundamental Mechanisms of Hydraulic Fracturing, PhD thesis, 2006''' | ||
** 2D discrete element method with bonded particle model (BPM) | ** 2D discrete element method with bonded particle model (BPM) | ||
** Cundal's model for fluid flow is described | ** Cundal's model for fluid flow is described | ||
| + | |||
=== Моделирование динамики проппанта === | === Моделирование динамики проппанта === | ||
| − | The transport and placement of proppant within the fracture is usually modeled by representing the slurry (i.e., the mixture of proppant and fluid) as a two-component, interpenetrating continuum. The distribution of proppant in the fracture is given by its volumetric concentration (defined as the probability of finding a proppant particle at a given point in space and time), which is the additional variable to be determined. In modeling proppant transport and placement, it is often assumed that: | + | * '''Adachi J., Siebrits E., Peirce A., Desroches J. Computer simulation of hydraulic fractures // Int. J. of Rock Mechanics & Mining Sciences, 44, 2007, pp. 739–757 ([[Медиа: Adachi_SimulHydrFrac.pdf |download, pdf]])''' The transport and placement of proppant within the fracture is usually modeled by representing the slurry (i.e., the mixture of proppant and fluid) as a two-component, interpenetrating continuum. The distribution of proppant in the fracture is given by its volumetric concentration (defined as the probability of finding a proppant particle at a given point in space and time), which is the additional variable to be determined. In modeling proppant transport and placement, it is often assumed that: |
| − | * both proppant and fluid are incompressible; | + | ** both proppant and fluid are incompressible; |
| − | * the proppant particles are small compared to a characteristic lengthscale, in this case the fracture width; | + | ** the proppant particles are small compared to a characteristic lengthscale, in this case the fracture width; |
| − | * the only mechanism to account for ‘‘slip’’ between the proppant and the carrying fluid is gravity-induced settling, i.e., relative proppant-fluid velocities due to migration by self-diffusion (created by shearing and/or proppant collision), Taylor dispersion, or clustering are usually neglected. This implies that, in the absence of gravity, the proppant and fluid move at the same velocity at any given point. | + | ** the only mechanism to account for ‘‘slip’’ between the proppant and the carrying fluid is gravity-induced settling, i.e., relative proppant-fluid velocities due to migration by self-diffusion (created by shearing and/or proppant collision), Taylor dispersion, or clustering are usually neglected. This implies that, in the absence of gravity, the proppant and fluid move at the same velocity at any given point. |
| − | * interaction and collision between proppant particles, shearinduced proppant migration, proppant settling, etc. | + | ** interaction and collision between proppant particles, shearinduced proppant migration, proppant settling, etc. |
| + | |||
| + | |||
| + | * '''H. Huang, Z. Xu, T. Wood, C. Palmer, E. Mattson Modeling of mechanical interactions of proppant and hydraulic fractures for in-situ oil shale retorting // abstract.''' Several in-situ oil shale retorting strategies require creation of either vertical or horizontal hydraulic fractures and injection of proppant to facilitate the flow of generated hydrocarbon fluid. An important issue is to reliably model the mechanical interactions between proppants and hydraulic fractures during heating and to quantify/predict the degree of proppant embedment into the shale matrix and associated reduction in fracture aperture under both thermal stress and confining stress (i.e. overburden). An extended 2D discrete element model (DEM) that incorporates the effect of plastic deformation of oil shale was developed and applied to the problem of modeling proppant-fracture mechanical interactions. The softening of the shale rock due to retorting and the development of localized plasticity zones near the surface of fracture walls was shown to be critical to the degree of proppant embedment and fracture closure. The 2D DEM model was carefully calibrated to realistic shale and proppant mechanical properties. Sensitivity studies were performed to systematically investigate the effects of mechanical properties of oil shale and proppants, proppant size, fracture closing stress, on the degree of proppant embedment into the shale formation and reduction of fracture aperture. The proppant size (diameter) has a significant effect on fracture closure. Greater average embedment and fracture closure were observed for the 20/40 proppant than for the smallest proppant (40/70) used in the sensitivity studies. These results suggest that the DEM model that includes plastic oil shale deformation is an effective predictive tool to quantify proppant embedment and the associated fracture aperture reduction under high temperature/stress environments representative of some proposed in-situ oil shale retorting strategies. | ||
| + | |||
| + | |||
| + | * '''ZHAO Zheng-chao, CUI Bin, YUE Yu-quan, Liao’he Oilfield, WANG Li-yang, WU Ying-xiang Numerical simulation of horizontal migration of proppant // Journal of Hydrodynamics, 2008'''.The horizontal migration of proppant was numerically investigated with a two-fluid model, in which the interaction between fracturing fluid and proppant, along with that among proppants was taken into account through interphase forces. The migration process and the volumetric concentration of the proppant were examined under various conditions, and the averaged volumetric concentration of the proppant was obtained. The present research might be useful in the process design of the hydraulic fracturing in the oilfields. | ||
| + | |||
| + | |||
| + | * '''P.B. Gadde, et al.The effect of proppant retardation on propped fracture length // SPE 97106, 2005.''' | ||
| + | ** Fracturing liquid and proppant are considered as two component liquid (slurry) | ||
| + | ** A model for velocity of proppant particle is presented. The particle is either accelerating or retarding relative to the fluid depending on the ratio particle size to the fracture width. | ||
| + | ** A model is presented for the effect of fracture walls and proppant concentration on proppant transport. A | ||
| + | ** New model for proppant retardation has been incorparated into 3D fracture simulator. | ||
| + | |||
| + | |||
| + | * '''Joseph D.D. Direct numerical simulation and models of proppant transport in fractured reservoirs // Report, 1998''' This GOALI proposal is for University based support for partnering between the fluid mechanics laboratory at the University of Minnesota and STIMLAB, which is a research laboratory in Duncan, OK supported by a consortium of oil production and oil service companies interested in reservoir stimulation. The proposal is to develop and apply direct numerical simulation (DNS) to problems of slurry transport in general and to proppant transport into reservoir fractures in particular. We aim to deliver a practical product to the fracturing industry in the form of (1) formulas for lift and drag on particles to be used by PC-based models of slurry transport and (2) correlations based on the processing of numerical experiments and real experiments using the same dimensionless parameters in log-log plots. | ||
| + | |||
| + | |||
| + | * ''''Joseph D.D. Direct Numerical Simulation of Slurry Transport Focusing on Engineering Correlations// Grant proposal, 2000.''' We have taken a major step toward development of two highly efficient parallel finite-element codes called particle movers for the direct numerical simulation of the motions of large numbers of solid particles in flows of Newtonian and viscoelastic fluids. One of the particle movers is based on moving unstructured meshes (Arbitrary Lagrangian-Eulerian or ALE) and the other (Distributed Lagrange Multiplier or DLM) on a structured mesh using a newmethod involving a distribution of Lagrange multipliers to ensure that the regions of space occupied by solids are in a rigid motion following Newton’s laws. The DLM particle mover evolved from well-known embedding methods and its potential for applications seems to be very great since the problems of remeshing, projection and so on which plague methods based on unstructured grids have been circumvented. On the other hand, the ALE methodology is well suited for problems in irregular domains and it is at present the only code in the world which can move solid particles in a viscoelastic fluid. By comparing results from these two codes on common problems, we are able to evaluate both. The research proposed under this KDI/NCC initiative has two goals. One is to develop state-of-the-art particle movers based on DNS; we aim to move thousands of particles in 3D slurry transport and fluidized bed calculations at the flow parameters relevant to applications. The second goal of our KDI/NCC research is to develop effective procedures for converting the results of DNS into forms which can be used in practical applications. One example of how to use DNS is the expansion of a fluidized bed. Sand transport in fractured oil and gas reservoirs is another system in which the ways that DNS can impact field operations is not obvious. In this system, the effects of microstructure at the particle level scale into particle placements in the fracture at the field level. We are going to focus our research on how to use DNS on this problem, partnering with oil and gas companies in the proppant (“prop open”) transport consortium STIMLAB. | ||
| + | |||
| + | == Возможные направления исследований == | ||
| + | |||
| + | 1. Выработка рекоммендаций по оптимизации свойств проппанта и технологии его доставки с целью увеличения продуктивности скважины | ||
| + | * разработка математических и компьютерных моделей для описания динамики проппанта в жидкости, используемой для гидроразрыва; | ||
| + | |||
| + | * валидация моделей, решение тестовых задач (динамика одиночной частицы в жидкости под действием гравитационногго поля, течение жидкости с проппантом в канале постоянного сечения); | ||
| + | |||
| + | * моделирование движения проппанта в трещине гидроразрыва; | ||
| + | |||
| + | * определение влияния параметров пропанта на стабилизацию трещин и повышение дебита скважины; | ||
| + | |||
| + | * исследование изменения проницаемости канала при высоких концентрациях проппанта (proppant bridges); | ||
| + | |||
| + | * моделирование динамики пропанта при прекращении закачки жидкости в скважину; | ||
| + | |||
| + | |||
| + | 2. Выработка рекомендации по оптимизации процесса гидроразрыва с учетом различных геофизических факторов | ||
| + | |||
| + | * разработка моделей разрушения горной породы под действием жидкости на основе континуальных подходов; | ||
| + | |||
| + | * разработка моделей на основе [[Метод динамики частиц | метода динамики частиц]] для описания деформирования и разрушения горной породы с учетом начальной деффектной структуры породы; | ||
| + | |||
| + | * моделирование развития трещин в горной породе под действием давления, создаваемого жидкостью (без учета динамики жидкости); | ||
| + | |||
| + | * сравнение с известными моделями (PKN, KGD, модель Олсона), определение параметров данных моделей на основе компьютерных расчетов; | ||
| + | |||
| + | * разработка модели течения жидкости в трещинах гидроразрыва с учетом изменяющейся геометрии трещин; | ||
| + | |||
| + | * моделирование гидроразрыва пласта с учетом динамики жидкости в трещинах гидроразрыва. | ||
| + | |||
| + | == Справочные материалы: лекционные курсы, обзорные статьи, презентации == | ||
| + | * Adachi J., Siebrits E., Peirce A., Desroches J. Computer simulation of hydraulic fractures // Int. J. of Rock Mechanics & Mining Sciences, 44, 2007, pp. 739–757 ([[Медиа: Adachi_SimulHydrFrac.pdf |download, pdf]]) | ||
| + | * Čikeš M. A short reservoir stimulation course. Lecture notes, 1996. ([[Медиа: A_SHORT_RESERVOIR_STIMULATION_COURSE.pdf |download, pdf]]) | ||
| + | * Dusseault M., McLennan J. Massive Multi-Stage Hydraulic Fracturing: Where are We? // preprint, ([[Медиа: Review_Massive_Multi-Stage_Hydraulic_Fracturing_Where_are_We.pdf |download, pdf]]) | ||
| + | * Barree R.D. Horizontal Well Stimulation Optimization // presentation, Barree & Associates LLC, 2009 ([[Медиа: Horizontal_Well_Stimulation.pdf |download, pdf]]) | ||
| + | * Barree R.D. Modeling Fracture Geometry // presentation, Barree & Associates LLC, 2009 ([[Медиа: Modeling_Fracture_Geometry.pdf |download, pdf]]) | ||
| + | * Barree R.D. Modeling Frac‐Fluid Rheology & Leakoff // presentation, Barree & Associates LLC, 2009 ([[Медиа: Modeling_Frac-Fluid_Rheology_and_Leakoff.pdf |download, pdf]]) | ||
| + | * MFRAC (Meyer FRACturing Simulators) User's Guide ([[Медиа: MFRAC_User's_Guide.pdf |download, pdf]]) | ||
| + | * Аксаков А.В., Борщук О.С., Желтова И.С., Дедурин А.В., Калуджер З., Пестриков А.В., Торопов К.В. [https://www.pdf-archive.com/2016/11/28/c/ Корпоративный симулятор гидроразрыва пласта: от математической модели к программной реализации] | ||
| + | * Ахтямов А.А., Макеев Г.А., Байдюков К.Н., Муслимов У.С., Матвеев С.Н., Пестриков А.В.,Резаев С.Н. [https://www.pdf-archive.com/2018/05/27/------fra-simulator-rn-grid/ Корпоративный симулятор гидроразрыва пласта «РН-ГРИД»: от программной реализации к промышленному внедрению] | ||
| + | == См. также == | ||
| + | |||
| + | * [[Моделирование динамики проппанта в трещинах гидроразрыва]] | ||
| + | * [[Моделирование трещинообразования при гидроразрыве пласта]] | ||
| − | == | + | == Ссылки == |
| − | + | * [http://www.aem.umn.edu/Solid-Liquid_Flows Direct Simulation of the Motion of Particles in Flowing Liquids] | |
| + | * [http://www.carboceramics.com/fracpropt-software/ Fracpro - fracture stimulation software ] | ||
| + | * [http://www.mfrac.com/ MFRAC - simulation software] | ||
| + | * [http://barree.net/index.htm Consulting on Hydraulic Fracturing] | ||
| + | * [http://www.fracom.fi/ 2D симулятор развития трещин в горной породе методом граничных элементов (BEM)] | ||
| + | * [http://www.geo.umass.edu/faculty/cooke/fric2d/chapter2.html FRIC2C программа, основанная на Displacement Discontinuity Method] | ||
| + | * [http://www.waytogoto.com/wiki/index.php/Hydro-fracturing Hydro-fracturing] on WikiMarcellus | ||
| + | * [http://ru.wikipedia.org/wiki/%D0%93%D0%B8%D0%B4%D1%80%D0%BE%D1%80%D0%B0%D0%B7%D1%80%D1%8B%D0%B2_%D0%BF%D0%BB%D0%B0%D1%81%D1%82%D0%B0 Гидравлический разрыв пласта] (Википедия) | ||
| + | * [http://en.wikipedia.org/wiki/Hydraulic_fracturing Hydraulic fracturing] (Wikipedia) | ||
| + | * [http://en.wikipedia.org/wiki/Proppant Proppants and fracking fluids] (Wikipedia) | ||
| + | *[http://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D0%BC%D1%83%D0%BB%D1%8F%D1%82%D0%BE%D1%80_%D0%B3%D0%B8%D0%B4%D1%80%D0%BE%D1%80%D0%B0%D0%B7%D1%80%D1%8B%D0%B2%D0%B0_%D0%BF%D0%BB%D0%B0%D1%81%D1%82%D0%B0 Симулятор гидроразрыва пласта] (Википедия) | ||
[[Category: Научные проекты]] | [[Category: Научные проекты]] | ||
[[Category: Механика дискретных сред]] | [[Category: Механика дискретных сред]] | ||
Текущая версия на 03:27, 8 июня 2018
Кафедра "Теоретическая механика" > Моделирование гидроразрыва пласта
Моделирование гидроразрыва пласта
Содержание
- 1 Гидравлический разрыв пласта
- 2 Физические процессы, сопровождающие гидроразрыв
- 3 Проблемы и задачи, возникающие при использовании технологии гидроразрыва
- 4 Модели, используемые в литературе
- 5 Возможные направления исследований
- 6 Справочные материалы: лекционные курсы, обзорные статьи, презентации
- 7 См. также
- 8 Ссылки
Гидравлический разрыв пласта[править]
Гидроразры́в пласта́ (ГРП) — один из методов интенсификации работы нефтяных и газовых скважин и увеличения приёмистости нагнетательных скважин. Метод заключается в создании высокопроводимой трещины в целевом пласте для обеспечения притока добываемого флюида (газ, вода, конденсат, нефть либо их смесь) к забою скважины. Технология осуществления ГРП включает в себя закачку в скважину с помощью мощных насосных станций жидкости разрыва (гель, в некоторых случаях вода, либо кислота при кислотных ГРП) при давлениях выше давления разрыва нефтеносного пласта. Для поддержания трещины в открытом состоянии в терригенных коллекторах используется расклинивающий агент — проппант, в карбонатных — кислота, которая разъедает стенки созданной трещины.
A ‘‘typical’’ hydraulic fracturing treatment starts with the creation of an initial path for the fracture. This is usually achieved by a technique called ‘‘perforation’’ in which specially designed shaped-charges are blasted on the wellbore walls with given orientations, perforating the casing and creating finger-like holes or weak points in the hydrocarbon-laden formation. A viscous fluid is pumped inside the wellbore, inducing a steep rise in the pressure which eventually leads to the initiation of a fracture at the perforated interval. A ‘‘pad’’ of clean fluid is usually pumped first, to provide sufficient fracture width for the proppant that follows. Proppant is injected at a later stage as a suspension or slurry. The treatment usually takes place on a time-scale of tens of minutes to a few hours, depending upon the designed fracture size and volume of proppant to be placed. At the end of the treatment, when pumping stops, leak-off of the residual fracturing fluid into the porous reservoir allows the fracture surfaces to close onto the proppant pack under the action of the far-field compressive stresses.
Физические процессы, сопровождающие гидроразрыв[править]
Основные процессы:
- деформирование и разрушение горной породы под действием жидкости
- течение жидкости в трещинах гидроразрыва
- транспорт проппанта в трещинах гидроразрыва
Особенности "реального" процесса гидроразрыва:
- неоднорподность (в частности, слоистая структура) горной породы;
- изменения в величине и/или ориентации сжимающих пластовых напряжений (changes in magnitude and/or orientation of the in situ confining stresses);
- присутствие свободных порехностей;
- утечка жидкости, используемой для гидроразрыва, в горную породу либо наоборот приток жидкости в трещины из породы;
- влияние температуры и сдвига на реологические свойства разрушающей жидкости;
- закрытие трещин в следствие прекращения накачки жидкости, намеренной откачки жидкости или резкого изменения геометрии за счет образования трещин (разгрузка породы);
- гидроразрыв так называемых ‘‘мягких’’ пород, таких как слабо консолидированный песчанник (weakly consolidated sandstone).
Проблемы и задачи, возникающие при использовании технологии гидроразрыва[править]
- prediction of fracture geometry (предсказание геометрии трещины, т.е. её полудлины, высоты и ширины раскрытия)
- effective prevention of crack closure (выбор оптимальных свойств проппанта (размеров, плотности, механических свойств, проницаемости упаковки), а также технологии его введения в трещину гидроразрыва)
- optimal choice of fracturing fluid (жидкость должна обеспечивать эффективный транспорт проппанта, а частности, иметь достаточную вязкость. Кроме того, должна обеспечиваться быстрая откачка жидкости после завершения технологического процесса)
- fluid leak-off (утечка жидкости для гидроразрыва из скважины в прилегающую породу)
- avoid screenouts caused by proppant a bridging and holdup (частицы проппанта могут застревать в трещинах, образуя мостики, препятствующие течению жидкости, используемой для гидроразрыва, и/или добывемого флюида (нефти, газа и т.д.). В результате может существенно снижаться продуктивность скважины)
- proppant flowback (при прекращении закачки жидкости в скважину может происходить движение проппанта в обратном направлении)
Модели, используемые в литературе[править]
Для моделирования разрушения горной породы в процессе гидроразрыва используются как методы механики сплошной среды (ассимптотические методы, метод конечных элементов, метод граничных элементов), так и механики дискретных сред (метод дискретных элементов).
Континуальные подходы к моделированию гидроразрыва[править]
Основные континуальные модели, используемые в литературе для моделирования гидроразрыва:
2D Models
- Perkins‐Kern Nordgren (PKN)
- Khristianovich‐Geertsma‐DeKlerk (KGD)
- Penny‐Frac
- Displacement Discontinuity Model
Lumped Parameter Models
- FracPro
- FracPro‐PT
Pseudo‐3D Models
3D Models
- GOHFER
- N‐StimPlan
- Terra‐Frac
Некоторые статьи по гидроразрыву.
- Adachia J., Siebritsb E., Peircec A., Desroches J. Computer simulation of hydraulic fractures // Int. J. of Rock Mechanics & Mining Sciences, 44, 2007, pp. 739–757 (download, pdf). В статье дается обзор континуальных подходов к моделированию гидроразрыва. В частности, отмечается, что при использовании континуальных методов, как правило, вводятся следующие ограничения:
- материал резервуара (горной породы) считается линейно упругим;
- в случае слоистого резервуара слои считаются параллельными и идеально сопряженными;
- гидроразрыв происходит в одной вертикальной плоскости;
- принимается модель Ньютоновской жидкости или жидкости с степенным учавнением состояния;
Как правило, не учитывается:
- неупругое (пластическое) поведение породы;
- непараллельность и неидеальная сопряженность поверхностей слоев;
- реальная геометрия трещины;
- естественная трещиноватость породы;
- начальные неоднородные поля напряжений, вызванные, в частности, пористостью структуры.
- сжимаемость, пластичность, вязкоупругость жидкости. Считается, что в канале осуществляется течение Пуазеля;
- влияние утечки жидкости на давление внутри трещин.
- Olson J.E. Multi-fracture propagation modeling: Applications to hydraulic fracturing in shales and tight gas sands // 42nd US Rock Mechanics Symposium, 2008. The diagnostic data suggests that in some situations, complex, multistranded fracture zones or networks develop as a result of interaction between the hydraulic fracture and pre-existing natural fractures. This paper examines complex hydraulic fracture pattern development using techniques previously applied to the analysis of natural fracture network development and the fracture of silicon wafers in microchip manufacture. The numerical code is based on a pseudo-3d displacement discontinuity solution, where the propagation of hundreds of fracture tips can be tracked simultaneously, with propagation velocities proportional to the stress intensity factor at each crack tip. The method does not yet solve for flow through the hydraulic fracture network, but instead uses a simplified constant pressure boundary condition for all fracture segments connected to the wellbore, enabling a preliminary analysis of this complex problem.
- Lin J., Zhu D. Predicting well performance in complex fracture systems by slab source method // SPE Hydraulic fracturing conference, 2012. The model for the flow inside fracture pattern is proposed.
- Fu P., Johnson S.M., Hao Y., Carrigan C.R. Fully coupled geomechanics and discrete flow network modeling of hydraulic fracturing for geothermal applications // Proc. of 36 Workshop on Geothermal Reservoir Engineering. The primary objective of our current research is to develop a computational test bed for evaluating borehole techniques to enhance fluid flow and heat transfer in enhanced geothermal systems (EGS). Simulating processes resulting in hydraulic fracturing and/or the remobilization of existing fractures, especially the interaction between propagating fractures and existing fractures, represents a critical goal of our project. To this end, we are continuing to develop a hydraulic fracturing simulation capability within the Livermore Distinct Element Code (LDEC), a combined FEM/DEM analysis code with explicit solid-fluid mechanics coupling. LDEC simulations start from an initial fracture distribution which can be stochastically generated or upscaled from the statistics of an actual fracture distribution. During the hydraulic stimulation process, LDEC tracks the propagation of fractures and other modifications to the fracture system. The output is transferred to the Non-isothermal Unsaturated Flow and Transport (NUFT) code to capture heat transfer and flow at the reservoir scale.
Дискретные подходы к моделированию гидроразрыва[править]
Резюме
Для дискретного моделирования процесса гидроразрыва в литературе, как правило, применяется метод дискретных элементов (DEM). При этом горная порода представляется в виде "связанных" (bonded) частиц, как правило, сферической формы. Для описания взаимодействий между частицами (связей) используется модель Bonded Particle Model (BPM), реже модель упругого стержня, соединяющего центры частиц. Для описания течения жидкости в трещинах гидроразрыва применяется модель, изложенная в Shimizu Y. Fixed coarse-grid fluid scheme in PFC2D, Itasca Consulting Group, Inc., Minnesota, 2008.
Приведем выдержки из некоторых статей по дискретному моделирвоанию гидроразрыва.
- Torres S.A.G., Castaño J.D.M. Simulation of the hydraulic fracture process in two dimensions using a discrete element method// Phys. Rev. E 75, 066109, 2007. We introduce a discrete element simulation for the hydraulic fracture process in a petroleum well which takes into account the elastic behavior of the rock and the Mohr-Coulomb fracture criteria. The rock is modeled as an array of Voronoi polygons joined by elastic beams, which are submitted to tectonical stresses and the hydrostatic pressure of the fracturing fluid. The fluid pressure is treated like that of a hydraulic column. We also include an analysis of the fracturing fluid loss due to the permeability of the rock which is useful in an efficiency analysis of the treatment.
- S. Deng, R. Podgorney, H. Huang, Discrete Element Modeling of rock deformation, fracture network development, permeability evolution under hydraulic stimulation // Proc. 36 Workshop on Geothermal reservoir engineering, 2011.
- 3D discrete element method with bonded particle model (BPM)
- two way coupling with fluid dynamics (model for network fluid flow)
- J.P. Pruiksma, A. Bezuijen Hydraulic fracturing with distinct element method // Report of DELFRAC consortium, 2002. In this report, hydraulic fracturing is investigated using the distinct element code PFC2D from Itasca. Special routines adding fluid flow to PFC2D and updating the fluid flow domains when fractures appear. After the set-up of the hydraulic fracturing simulations has been discussed, with all the main input parameters, several main parameters are varied to study the resulting fracture patterns, pressure distributions and borehole pressures. These parameter studies are: particle size dependency of the simulations, behaviour at various confining stresses, the influence of the internal friction angle of the sand and the fracturing behaviour for different borehole injection rates. After this parameter study, comparisons are made with experiments done at TU Delft, GeoDelft and in the literature. The simulation results show the same trends as the experiments and are also in good agreement quantitatively (2D discrete element method with bonded particle model (BPM))
- H. Shimizu, T.Koyama, S. Murata, T. Ishida, M. Chijimatsu, T. Fujita, S. Nakama Distinct element modeling for Class II behavior of rock and hydraulic fracturing // International Journal of the JCRM vol.7, 2011, pp.33-36. Newly developed numerical approaches using the Distinct Element Method (DEM) were presented, and a series of DEM simulations were performed for better understanding the physical phenomena and mechanism for the following two fundamental issues in rock engineering field. The first issue is the Class II behavior of the brittle rocks under uniaxial compression. The radial strain control method for uniaxial compression tests was introduced in the DEM codes and the Class II behavior of rocks was simulated. The simulation results suggest that the DEM can reproduce the Class II behavior of the rock successfully and revealed that the loading condition of rocks (radial strain control) will play an important role for the Class II behavior. The second issue is the hydraulic fracturing behavior in rocks. A series of simulations for hydraulic fracturing in rock was performed by using the flow-coupled DEM code. Simulation results clearly show that the fluid infiltration behavior depends on the fluid viscosity (2D discrete element method with bonded particle model (BPM))
- Park N. DE modeling of rock fracture behavior: fracture toughness and time-dependent fracture growth // PhD thesis, 2006.
- 3D discrete element method with bonded particle model (BPM)
- Cundal's model for fluid flow is used (unpublished)
- Wu R. Some Fundamental Mechanisms of Hydraulic Fracturing, PhD thesis, 2006
- 2D discrete element method with bonded particle model (BPM)
- Cundal's model for fluid flow is described
Моделирование динамики проппанта[править]
- Adachi J., Siebrits E., Peirce A., Desroches J. Computer simulation of hydraulic fractures // Int. J. of Rock Mechanics & Mining Sciences, 44, 2007, pp. 739–757 (download, pdf) The transport and placement of proppant within the fracture is usually modeled by representing the slurry (i.e., the mixture of proppant and fluid) as a two-component, interpenetrating continuum. The distribution of proppant in the fracture is given by its volumetric concentration (defined as the probability of finding a proppant particle at a given point in space and time), which is the additional variable to be determined. In modeling proppant transport and placement, it is often assumed that:
- both proppant and fluid are incompressible;
- the proppant particles are small compared to a characteristic lengthscale, in this case the fracture width;
- the only mechanism to account for ‘‘slip’’ between the proppant and the carrying fluid is gravity-induced settling, i.e., relative proppant-fluid velocities due to migration by self-diffusion (created by shearing and/or proppant collision), Taylor dispersion, or clustering are usually neglected. This implies that, in the absence of gravity, the proppant and fluid move at the same velocity at any given point.
- interaction and collision between proppant particles, shearinduced proppant migration, proppant settling, etc.
- H. Huang, Z. Xu, T. Wood, C. Palmer, E. Mattson Modeling of mechanical interactions of proppant and hydraulic fractures for in-situ oil shale retorting // abstract. Several in-situ oil shale retorting strategies require creation of either vertical or horizontal hydraulic fractures and injection of proppant to facilitate the flow of generated hydrocarbon fluid. An important issue is to reliably model the mechanical interactions between proppants and hydraulic fractures during heating and to quantify/predict the degree of proppant embedment into the shale matrix and associated reduction in fracture aperture under both thermal stress and confining stress (i.e. overburden). An extended 2D discrete element model (DEM) that incorporates the effect of plastic deformation of oil shale was developed and applied to the problem of modeling proppant-fracture mechanical interactions. The softening of the shale rock due to retorting and the development of localized plasticity zones near the surface of fracture walls was shown to be critical to the degree of proppant embedment and fracture closure. The 2D DEM model was carefully calibrated to realistic shale and proppant mechanical properties. Sensitivity studies were performed to systematically investigate the effects of mechanical properties of oil shale and proppants, proppant size, fracture closing stress, on the degree of proppant embedment into the shale formation and reduction of fracture aperture. The proppant size (diameter) has a significant effect on fracture closure. Greater average embedment and fracture closure were observed for the 20/40 proppant than for the smallest proppant (40/70) used in the sensitivity studies. These results suggest that the DEM model that includes plastic oil shale deformation is an effective predictive tool to quantify proppant embedment and the associated fracture aperture reduction under high temperature/stress environments representative of some proposed in-situ oil shale retorting strategies.
- ZHAO Zheng-chao, CUI Bin, YUE Yu-quan, Liao’he Oilfield, WANG Li-yang, WU Ying-xiang Numerical simulation of horizontal migration of proppant // Journal of Hydrodynamics, 2008.The horizontal migration of proppant was numerically investigated with a two-fluid model, in which the interaction between fracturing fluid and proppant, along with that among proppants was taken into account through interphase forces. The migration process and the volumetric concentration of the proppant were examined under various conditions, and the averaged volumetric concentration of the proppant was obtained. The present research might be useful in the process design of the hydraulic fracturing in the oilfields.
- P.B. Gadde, et al.The effect of proppant retardation on propped fracture length // SPE 97106, 2005.
- Fracturing liquid and proppant are considered as two component liquid (slurry)
- A model for velocity of proppant particle is presented. The particle is either accelerating or retarding relative to the fluid depending on the ratio particle size to the fracture width.
- A model is presented for the effect of fracture walls and proppant concentration on proppant transport. A
- New model for proppant retardation has been incorparated into 3D fracture simulator.
- Joseph D.D. Direct numerical simulation and models of proppant transport in fractured reservoirs // Report, 1998 This GOALI proposal is for University based support for partnering between the fluid mechanics laboratory at the University of Minnesota and STIMLAB, which is a research laboratory in Duncan, OK supported by a consortium of oil production and oil service companies interested in reservoir stimulation. The proposal is to develop and apply direct numerical simulation (DNS) to problems of slurry transport in general and to proppant transport into reservoir fractures in particular. We aim to deliver a practical product to the fracturing industry in the form of (1) formulas for lift and drag on particles to be used by PC-based models of slurry transport and (2) correlations based on the processing of numerical experiments and real experiments using the same dimensionless parameters in log-log plots.
- 'Joseph D.D. Direct Numerical Simulation of Slurry Transport Focusing on Engineering Correlations// Grant proposal, 2000. We have taken a major step toward development of two highly efficient parallel finite-element codes called particle movers for the direct numerical simulation of the motions of large numbers of solid particles in flows of Newtonian and viscoelastic fluids. One of the particle movers is based on moving unstructured meshes (Arbitrary Lagrangian-Eulerian or ALE) and the other (Distributed Lagrange Multiplier or DLM) on a structured mesh using a newmethod involving a distribution of Lagrange multipliers to ensure that the regions of space occupied by solids are in a rigid motion following Newton’s laws. The DLM particle mover evolved from well-known embedding methods and its potential for applications seems to be very great since the problems of remeshing, projection and so on which plague methods based on unstructured grids have been circumvented. On the other hand, the ALE methodology is well suited for problems in irregular domains and it is at present the only code in the world which can move solid particles in a viscoelastic fluid. By comparing results from these two codes on common problems, we are able to evaluate both. The research proposed under this KDI/NCC initiative has two goals. One is to develop state-of-the-art particle movers based on DNS; we aim to move thousands of particles in 3D slurry transport and fluidized bed calculations at the flow parameters relevant to applications. The second goal of our KDI/NCC research is to develop effective procedures for converting the results of DNS into forms which can be used in practical applications. One example of how to use DNS is the expansion of a fluidized bed. Sand transport in fractured oil and gas reservoirs is another system in which the ways that DNS can impact field operations is not obvious. In this system, the effects of microstructure at the particle level scale into particle placements in the fracture at the field level. We are going to focus our research on how to use DNS on this problem, partnering with oil and gas companies in the proppant (“prop open”) transport consortium STIMLAB.
Возможные направления исследований[править]
1. Выработка рекоммендаций по оптимизации свойств проппанта и технологии его доставки с целью увеличения продуктивности скважины
- разработка математических и компьютерных моделей для описания динамики проппанта в жидкости, используемой для гидроразрыва;
- валидация моделей, решение тестовых задач (динамика одиночной частицы в жидкости под действием гравитационногго поля, течение жидкости с проппантом в канале постоянного сечения);
- моделирование движения проппанта в трещине гидроразрыва;
- определение влияния параметров пропанта на стабилизацию трещин и повышение дебита скважины;
- исследование изменения проницаемости канала при высоких концентрациях проппанта (proppant bridges);
- моделирование динамики пропанта при прекращении закачки жидкости в скважину;
2. Выработка рекомендации по оптимизации процесса гидроразрыва с учетом различных геофизических факторов
- разработка моделей разрушения горной породы под действием жидкости на основе континуальных подходов;
- разработка моделей на основе метода динамики частиц для описания деформирования и разрушения горной породы с учетом начальной деффектной структуры породы;
- моделирование развития трещин в горной породе под действием давления, создаваемого жидкостью (без учета динамики жидкости);
- сравнение с известными моделями (PKN, KGD, модель Олсона), определение параметров данных моделей на основе компьютерных расчетов;
- разработка модели течения жидкости в трещинах гидроразрыва с учетом изменяющейся геометрии трещин;
- моделирование гидроразрыва пласта с учетом динамики жидкости в трещинах гидроразрыва.
Справочные материалы: лекционные курсы, обзорные статьи, презентации[править]
- Adachi J., Siebrits E., Peirce A., Desroches J. Computer simulation of hydraulic fractures // Int. J. of Rock Mechanics & Mining Sciences, 44, 2007, pp. 739–757 (download, pdf)
- Čikeš M. A short reservoir stimulation course. Lecture notes, 1996. (download, pdf)
- Dusseault M., McLennan J. Massive Multi-Stage Hydraulic Fracturing: Where are We? // preprint, (download, pdf)
- Barree R.D. Horizontal Well Stimulation Optimization // presentation, Barree & Associates LLC, 2009 (download, pdf)
- Barree R.D. Modeling Fracture Geometry // presentation, Barree & Associates LLC, 2009 (download, pdf)
- Barree R.D. Modeling Frac‐Fluid Rheology & Leakoff // presentation, Barree & Associates LLC, 2009 (download, pdf)
- MFRAC (Meyer FRACturing Simulators) User's Guide (download, pdf)
- Аксаков А.В., Борщук О.С., Желтова И.С., Дедурин А.В., Калуджер З., Пестриков А.В., Торопов К.В. Корпоративный симулятор гидроразрыва пласта: от математической модели к программной реализации
- Ахтямов А.А., Макеев Г.А., Байдюков К.Н., Муслимов У.С., Матвеев С.Н., Пестриков А.В.,Резаев С.Н. Корпоративный симулятор гидроразрыва пласта «РН-ГРИД»: от программной реализации к промышленному внедрению
См. также[править]
- Моделирование динамики проппанта в трещинах гидроразрыва
- Моделирование трещинообразования при гидроразрыве пласта
Ссылки[править]
- Direct Simulation of the Motion of Particles in Flowing Liquids
- Fracpro - fracture stimulation software
- MFRAC - simulation software
- Consulting on Hydraulic Fracturing
- 2D симулятор развития трещин в горной породе методом граничных элементов (BEM)
- FRIC2C программа, основанная на Displacement Discontinuity Method
- Hydro-fracturing on WikiMarcellus
- Гидравлический разрыв пласта (Википедия)
- Hydraulic fracturing (Wikipedia)
- Proppants and fracking fluids (Wikipedia)
- Симулятор гидроразрыва пласта (Википедия)