Integrating Rotational Degree Of Freedom in EDEM — различия между версиями
Aleste (обсуждение | вклад) (→Contact Model) |
Aleste (обсуждение | вклад) (→Additional Measures) |
||
| Строка 57: | Строка 57: | ||
Файл:EDEM_Kin_Energy.jpg | Файл:EDEM_Kin_Energy.jpg | ||
</gallery> | </gallery> | ||
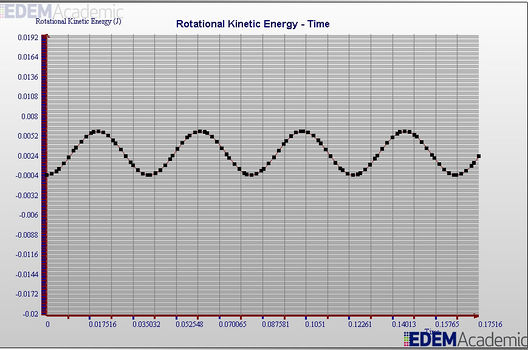
| + | As we can see Kinetic energy is conserved. | ||
Версия 18:55, 15 февраля 2012
Содержание
Task
Understand - how rotational DOF are integrated inside EDEM. For this: prepare simulation which could be compared with analytics.
For this:
- Prepare factory that creates particles
- Prepare contact model which describes the rule of interaction
- Prepare EDEM simulation
- Measure something and compare it to analytic
Who we are
- Степанов Алексей (responsible for contact model)
- Дзенушко Дайнис (responsible for factory and EDEM simulation)
Factory
We create 2 particles on a distance 0.1m and rotated at an angle of 5-15 () degrees;
These particles are of 2 types "small" and a "big" one; Big particle has identity matrix as rotation matrix; Small particle is rotated using rotation matrix
Particles's velocity and angular velocity equals to zero;
Y and Z coordinates are the same (0.5,0.5); Only X is different (0.45 for "big" and 0.55 for "small");
- For small particle:
double OrientAngle = pi/12; // angle between particles in Radians
orientation[0] = 1.0; // Rotating particle. X axis.
orientation[4] = cos(OrientAngle);
orientation[5] = -sin(OrientAngle);
orientation[7] = sin(OrientAngle);
orientation[8] = cos(OrientAngle);
Contact Model
In our project we used simple contact model.
All central forces we made zero. Also we made zero all torques except torque, which operates on a "small" particle.
calculatedElem2AdditionalTorqueX = 1.0 * (elem1Orientation[7] * elem2Orientation[4] + elem2Orientation[5] * elem1Orientation[4] );
In this formula С = 1.0
EDEM simulation
Globals:
Interaction: Particle to particle
Model: our contact model
No gravity
There are two materials "material" and "material_2" with different density for "material" 1000 for "material_2" 1.7e+05
Restitution: 0.5
No static and rolling friction
Particles:
We create particles of 2 types;"big" with big moment of inertia (100kgm2 X-axis) and "small"(0.000285kgm2 X-axis);Both particles are made of 2 surfaces placed along Z-axis on a distance of 2 particle radius
Measures
We measured the period of oscillation
Analytics
Integration
We measured period using the Graph of angular velocity and got the result
Results
So we got the result that is different to the analytic;
Then we wrote small programm on C# that integrates the equalation in a simple way and got the result
We checked all in EDEM simulation; Changing parameters of particles, roll stiffness didn't gave any difference the results stayed different to analytic.
Additional Measures
We chacked translational kinetic and potentional energy and they really equals to zero
Graph of Rotational Kinetic energy
As we can see Kinetic energy is conserved.