КП: Динамика требушета — различия между версиями
Tanya (обсуждение | вклад) (→Результат) |
(подставлены примерно правильные пропорции требушета) |
||
| (не показано 13 промежуточных версий 4 участников) | |||
| Строка 15: | Строка 15: | ||
== Постановка задачи == | == Постановка задачи == | ||
Дано: <br> | Дано: <br> | ||
| − | Масса противовеса M = | + | Масса противовеса M = 15т; <br> |
| − | Масса ядра m = | + | Масса ядра m = 300кг; <br> |
Масса рычага m_b = 100кг;<br> | Масса рычага m_b = 100кг;<br> | ||
| − | Длина большего плеча рычага l1 = | + | Длина большего плеча рычага l1 = 50м; <br> |
| − | Длина меньшего плеча рычага l2 = | + | Длина меньшего плеча рычага l2 = 10м; <br> |
Длина пращи l3 = 0.6м; <br> | Длина пращи l3 = 0.6м; <br> | ||
1.Рассчитать максимальную скорость полета ядра в упрощенной задаче (без пращи) <br> | 1.Рассчитать максимальную скорость полета ядра в упрощенной задаче (без пращи) <br> | ||
| Строка 45: | Строка 45: | ||
Рассмотрим систему с пращой:<br> | Рассмотрим систему с пращой:<br> | ||
[[Файл: 137763394_329869411.jpg|250px]]<br> | [[Файл: 137763394_329869411.jpg|250px]]<br> | ||
| − | + | Выберем обобщенные координаты <math> </math> и <math> \psi </math>. Применяя уравнение Лагранжа 2-го рода, получили: | |
| − | Выберем обобщенные координаты <math> | + | [[Файл: TanyaF1.jpg]]<br> |
| − | + | [[Файл: TanyaF2.jpg]]<br> | |
| − | <math> | + | Решили данную систему с помощью численного интегрирования.За условие отрыва возьмем <math> \psi \approx \pi </math>.<br> |
| − | + | При <math> \psi = 3.18389 </math> <math> \varphi = 2.41154 </math> и скорость ядра <math> V_{m} = 17.6007 </math> м/c.<br> | |
| − | <math> | + | <gallery> |
| − | + | Файл:Trebuchet_psi.JPG|График <math>\psi</math>(t) | |
| − | + | Файл:Trebuchet_phi.JPG|График <math>\varphi</math>(t) | |
| − | В результате получили,что скорость ядра в системе без пращи | + | </gallery> |
| + | В результате получили,что скорость ядра в системе без пращи меньше,чем в системе с пращой. | ||
== Ссылки по теме == | == Ссылки по теме == | ||
Текущая версия на 05:08, 20 апреля 2023
А.М. Кривцов > Теоретическая механика > Курсовые проекты 2014 > Динамика требушетаКурсовой проект по Теоретической механике
Исполнитель: Теницкая Татьяна
Группа: 08 (23604)
Семестр: весна 2014
Содержание
Аннотация проекта[править]
Данный проект посвящен изучению строения и принципа работы требюше.
Требушет,а также требюше (от фр. trébuchet — «весы с коромыслом») — метательная машина гравитационного действия.Применялись такие машины в средневековье для осады городов.
Постановка задачи[править]
Дано:
Масса противовеса M = 15т;
Масса ядра m = 300кг;
Масса рычага m_b = 100кг;
Длина большего плеча рычага l1 = 50м;
Длина меньшего плеча рычага l2 = 10м;
Длина пращи l3 = 0.6м;
1.Рассчитать максимальную скорость полета ядра в упрощенной задаче (без пращи)
2.Рассчитать максимальную скорость полета ядра в задаче с пращой
3.Сравнить скорости,найденные в первой и второй задачах, сделать выводы
Общие сведения по теме[править]
Принцип работы требюше:
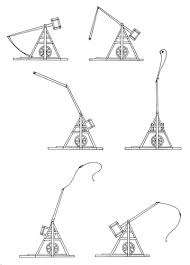
Принцип его действия основан на использовании энергии падающего груза большой массы, закреплённого на коротком конце рычага. При этом длинный конец рычага разгоняет пращу со снарядом до большой скорости. Отличительной особенностью является механизм автоматического раскрытия пращи требушета, когда происходит выстрел и снаряд начинает самостоятельное перемещение. Длинный рычаг требушета соединен с двумя веревками пращи: один конец постоянно привязан к рычагу, второй в виде петли накидывается на конец рычага, на котором устроен крюк. Во время выстрела, когда праща набрала скорость, а перекладина с противовесом, проделав основной путь, начинает замедляться, концы пращи начинают скользить вокруг длинного конца с крюком, пока один из концов не соскакивает с крюка, вследствие чего праща раскрывается.
Результат[править]
Рассмотрим систему без пращи:
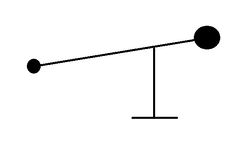
По закону сохранения энергии имеем:
Скорости определяются соотношением:
Получаем формулу для определения скорости ядра:
Из формулы видно,что максимальная скорость полета ядра будет при
Получили м/с
Рассмотрим систему с пращой:
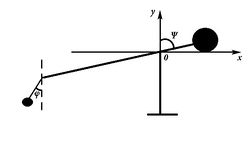
Выберем обобщенные координаты и . Применяя уравнение Лагранжа 2-го рода, получили:
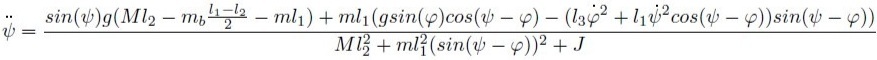
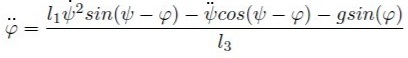
Решили данную систему с помощью численного интегрирования.За условие отрыва возьмем .
При и скорость ядра м/c.
В результате получили,что скорость ядра в системе без пращи меньше,чем в системе с пращой.

