Реализация симплектического метода для вращательного движения твердого тела — различия между версиями
| Строка 10: | Строка 10: | ||
==Постановка задачи== | ==Постановка задачи== | ||
Реализовать симплектический для вращательного движения твердого тела. | Реализовать симплектический для вращательного движения твердого тела. | ||
| + | |||
| + | Построить графики изменения полной энергии системы. Убедиться в симплектичности метода. | ||
==Теория== | ==Теория== | ||
| + | Данный метод был получен Девидом Финчамом как аналог метода Верле для вращательного движения. Для описания поворота в данной статье используются кватернионы. | ||
| + | Алгоритм состоит из двух частей. | ||
| + | |||
| + | Вспомогательная часть: | ||
| + | |||
| + | <math> | ||
| + | 1.\: \underline{J}^{n} = \underline{J}^{n-1/2} +\frac{1}{2}\Delta t \: \underline{T}^{n} | ||
| + | \\ | ||
| + | 2. \: \underline{J}^{n}_{p} = \underline{\underline{A}}^{n} \: \underline{J}^{n} | ||
| + | \\ | ||
| + | 3.\: \omega_{pi}^{n} = {J}^{n}_{pi}/I | ||
| + | \\ | ||
| + | 4.\: \underline{q}^{n+1/2}=\underline{q}^{n}+\frac{1}{2}\Delta t \: \underline{\underline{Q}}^{n}\underline{\omega}_{p}^{n} | ||
| + | \\ | ||
| + | 5.\: Использовать\: \underline{q}^{n+1/2}\: для\: вычисления\: \underline{\underline{A}}^{n+1/2} \: и\: \underline{\underline{Q}}^{n+1/2}. | ||
| + | </math> | ||
| + | |||
| + | Главная часть: | ||
| + | |||
| + | <math> | ||
| + | 6.\: \underline{J}^{n+1/2} = \underline{J}^{n-1/2} +\Delta t \: \underline{T}^{n} | ||
| + | \\ | ||
| + | 7.\: \underline{J}^{n+1/2}_{p} = \underline{\underline{A}}^{n+1/2} \: \underline{J}^{n} | ||
| + | \\ | ||
| + | 8.\: \omega_{pi}^{n_1/2} = {J}^{n+1/2}_{pi}/I | ||
| + | \\ | ||
| + | 9.\: \underline{q}^{n+1}=\underline{q}^{n}+\Delta t \: \underline{\underline{Q}}^{n+1/2}\underline{\omega}_{p}^{n+1/2} | ||
| + | \\ | ||
| + | 10. \: Сохранить \: \underline{J}^{n+1/2} \: и \: \underline{q}^{n+1} \: для\: следующих\: шагов. | ||
| + | </math> | ||
| + | |||
| + | Где <math></math> | ||
==Результаты== | ==Результаты== | ||
| + | Алгоритм был реализован на языке программирования Python. | ||
| + | |||
| + | В качестве модели для расчета был взят куб закрепленный пружинами на углах с заданным начальным поворотом. | ||
| + | |||
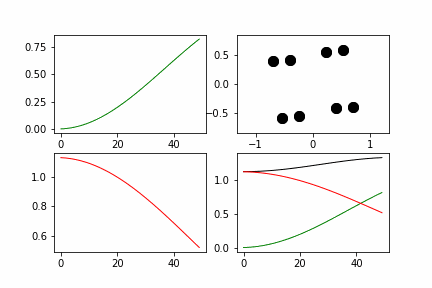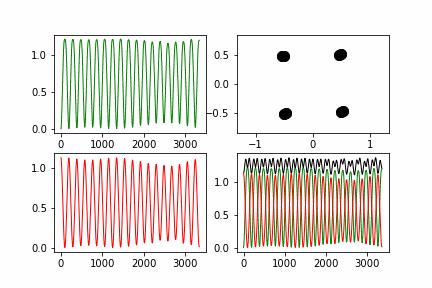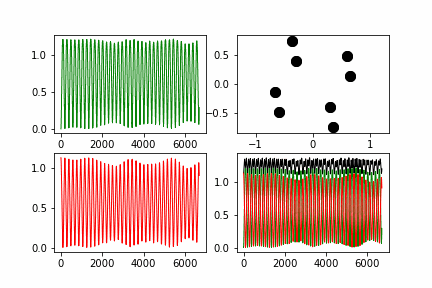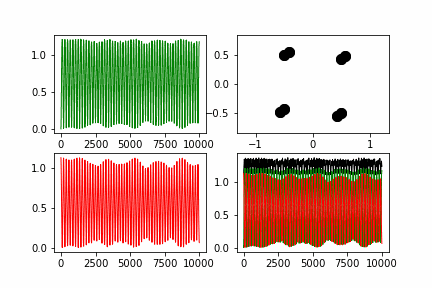
| + | Полученные графики: | ||
| + | |||
| + | [[File:Symplecticint1.gif]] | ||
| + | |||
| + | Здесь красная линия - потенциальная энергия системы, зеленая - кинетическая, черная - полная. | ||
| + | |||
| + | Как можно заметить полная энергия системы не растет со временем, а лишь колеблется около одного значения. В данном случае, отклонения не превышают 5% от среднего значения. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Ссылки== | ||
| + | 1. D. Fincham, Mol. Simul. 8, 165 (1992). | ||
Версия 22:07, 23 января 2020
Курсовой проект по Механике дискретных сред
Исполнитель: Ершов Александр
Группа: 3630103/60101
Семестр: осень 2019
Содержание
Постановка задачи
Реализовать симплектический для вращательного движения твердого тела.
Построить графики изменения полной энергии системы. Убедиться в симплектичности метода.
Теория
Данный метод был получен Девидом Финчамом как аналог метода Верле для вращательного движения. Для описания поворота в данной статье используются кватернионы. Алгоритм состоит из двух частей.
Вспомогательная часть:
Главная часть:
Где
Результаты
Алгоритм был реализован на языке программирования Python.
В качестве модели для расчета был взят куб закрепленный пружинами на углах с заданным начальным поворотом.
Полученные графики:
Здесь красная линия - потенциальная энергия системы, зеленая - кинетическая, черная - полная.
Как можно заметить полная энергия системы не растет со временем, а лишь колеблется около одного значения. В данном случае, отклонения не превышают 5% от среднего значения.
Ссылки
1. D. Fincham, Mol. Simul. 8, 165 (1992).