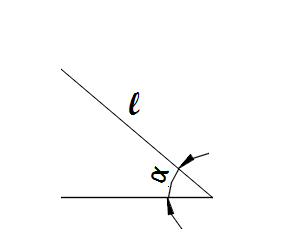Участник:MashinaG — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
(→‎Результаты по проекту)
(→‎Расчеты элементов проекта)
 
(не показано 14 промежуточных версий 4 участников)
Строка 25: Строка 25:
 
* Башаро Егор
 
* Башаро Егор
 
* Гончар Виталий
 
* Гончар Виталий
−
* Елизаров Андрей
 
 
* Красников Вячеслав
 
* Красников Вячеслав
−
* Кузнецов Николай
 
 
* Макеев Всеволод
 
* Макеев Всеволод
 
* Новикова Валентина
 
* Новикова Валентина
Строка 137: Строка 135:
  
 
==Расчеты элементов проекта==
 
==Расчеты элементов проекта==
−
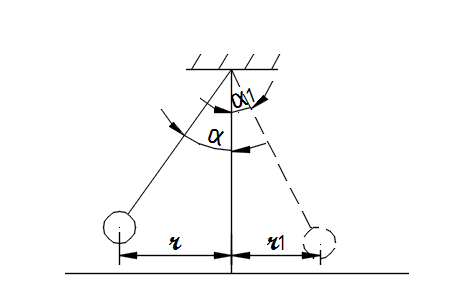
*Расчет расстояния и угла, на который необходимо отклонить маятник, чтобы он сбил домино
+
*Расчет расстояния и угла, на который необходимо отклонить маятник, чтобы он сбил домино(Надежда Новикова)
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible-content">  
 
<div class="mw-collapsible-content">  
−
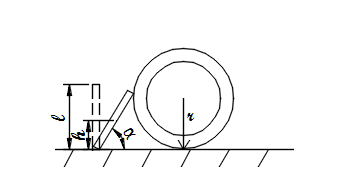
[[File:|thumb|]]
+
[[File:Расчет_расстояния_и_угла,_на_который_необходимо_отклонить_маятник,_чтобы_он_сбил_домино.png]]
−
<p>Дано:</p>
+
<br><math>Дано:</math>
 +
<br><math>r_1=0,04м </math>
 +
<br><math>l=0,15м</math>
  
−
<p>r_1=0,04м <br>
+
<br><math>Найти:α,r</math>
−
l=0,15м</p>
 
  
−
<p>Найти:α,r</p>
+
<br><math>Решение:</math>
 +
<br><math>r_1=lsinα_1</math>
 +
<br><math>α_1=arcsin⁡(r_1/l)</math>
 +
<br><math>α=3α_1=3 arcsin⁡〖(r_1/l)〗</math>
 +
<br><math>r=l(sin)_α=lsin⁡(3 arcsin⁡(r_1/l) )=0,15sin⁡(3 arcsin⁡(0,04/0,15) )=0,15sin⁡(3*15,466)=0,1086м</math>
 +
<br><math>α=3 arcsin⁡(0,02/0,07)=46,4°</math>
 +
<br><math>Ответ: r=0,1086м; α=46,4°</math>
  
−
<p>Решение:<br>
 
−
r_1=l∙sinα_1<br>
 
−
α_1=arcsin⁡(r_1/l)<br>
 
−
α=3α_1=3 arcsin⁡〖(r_1/l)〗<br>
 
−
r=l∙〖sin〗_α=l∙sin⁡(3 arcsin⁡(r_1/l) )=0,15∙sin⁡(3 arcsin⁡(0,04/0,15) )=0,15∙sin⁡(3∙15,466)=0,1086м<br>
 
−
α=3 arcsin⁡(0,02/0,07)=46,4°<br>
 
−
 
−
Ответ: r=0,1086м; α=46,4°<br>
 
−
</p>
 
 
</div>
 
</div>
 
</div>
 
</div>
  
  
−
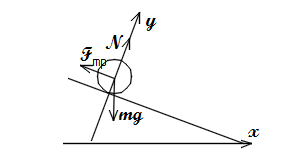
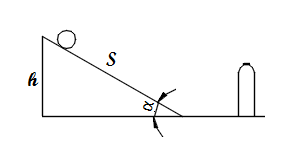
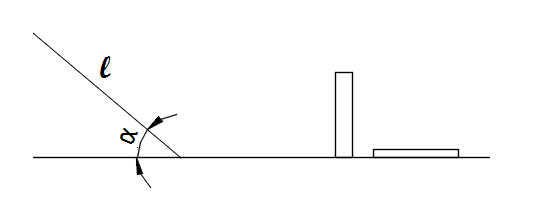
*Расчёт минимального угла наклона плоскости, при котором мяч-1 сможет катиться
+
*Расчёт минимального угла наклона плоскости, при котором мяч-1 сможет катиться (Алика Сигунова)
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible-content">  
 
<div class="mw-collapsible-content">  
−
[[File:|thumb|]]
+
[[File:Расчёт_минимального_угла_наклона_плоскости,_при_котором_мяч-1_сможет_катиться.png ]]
−
<p>Дано:</p>
+
<br><math>Дано:</math>
 +
<br><math>m=0,0585кг</math>
 +
<br><math>l=0,2м</math>
 +
<br><math>g=10м/с^2</math>
 +
<br><math>V_0=0м/с</math>
 +
<br><math>V=1,71м/с</math>
  
−
<p>m=0,0585кг<br>
+
<br><math>Найти: α</math>
−
l=0,2м<br>
 
−
g=10м/с^2<br>
 
−
V_0=0м/с<br>
 
−
V=1,71м/с<br>
 
  
−
Найти: α<br>
+
<br><math>Решение:</math>
 +
<br><math>Из закона сохранения энергии:</math>
 +
<br><math>E_(k*1)+E_(n*1)=E_(k*2)+E_(n*2)</math>
 +
<br><math>E_k1=0; E_n2=0</math>
 +
<br><math>E_n1=E_k2</math>
 +
<br><math>E_n=mgh</math>
 +
<br><math>E_k=(mv^2)/2</math>
 +
<br><math>mgh=(mv^2)/2</math>
 +
<br><math>h=v^2/2g</math>
 +
<br><math>h=〖1,71〗^2/20=0,146м</math>
 +
<br><math>α=arcsin⁡(h/l)</math>
 +
<br><math>α=arcsin⁡(0,146/0,2)≈47°</math>
 +
<br><math>Ответ: α≈47°</math>
  
−
Решение:<br>
 
−
Из закона сохранения энергии:<br>
 
−
E_(k∙1)+E_(n∙1)=E_(k∙2)+E_(n∙2)<br>
 
−
E_k1=0; E_n2=0<br>
 
−
E_n1=E_k2<br>
 
−
E_n=mgh<br>
 
−
E_k=(mv^2)/2<br>
 
−
mgh=(mv^2)/2<br>
 
−
h=v^2/2g<br>
 
−
h=〖1,71〗^2/20=0,146м<br>
 
−
α=arcsin⁡(h/l)<br>
 
−
α=arcsin⁡(0,146/0,2)≈47°<br>
 
−
Ответ: α≈47°<br>
 
−
<br>
 
−
</p>
 
  
 
</div>
 
</div>
Строка 195: Строка 189:
  
  
−
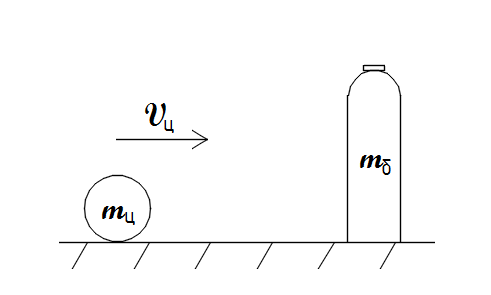
*Расчёт скорости, с которой должен катиться мяч-1, чтобы сбить стаканчики
+
*Расчёт скорости, с которой должен катиться мяч-1, чтобы сбить стаканчики (Егор Башаро)
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible-content">  
 
<div class="mw-collapsible-content">  
−
[[File:|thumb|]]
+
[[File:Расчёт_минимального_угла_наклона_плоскости,_при_котором_мяч-1_сможет_катиться.png ]]
−
<p>Дано:</p>
+
<br><math>Дано:</math>
  
−
<p>m_мяча=0,0585кг<br>
+
<br><math>m_мяча=0,0585кг</math>
−
m_(стак.)=0,01кг<br>
+
<br><math>m_(стак.)=0,01кг</math>
−
t=1c<br>
+
<br><math>t=1c</math>
  
−
Найти: v<br>
+
<br><math>Найти: v</math>
  
−
Решение: <br>
+
<br><math>Решение: </math>
−
p=F_взаим∙t<br>
+
<br><math>p=F_взаим∙t</math>
−
F_взаим>F_(т.ст.)=m_ст∙g=0,01∙10=0,1H<br>
+
<br><math>F_взаим>F_(т.ст.)=m_ст*g=0,01*10=0,1H</math>
−
p_мяча=m_мяча∙v<br>
+
<br><math>p_мяча=m_мяча*v</math>
−
v=P_м/m_м <br>
+
<br><math>v=P_м/m_м </math>
−
p_м=p=F_(т.стак)∙dt<br>
+
<br><math>p_м=p=F_(т.стак)*dt</math>
−
v=(F_(т.ст)∙dt)/m_мяча =(0,1 ∙1)/0,0585=1,71 м/с<br>
+
<br><math>v=(F_(т.ст)*dt)/m_мяча =(0,1 *1)/0,0585=1,71 м/с</math>
 +
 
 +
<br><math>Ответ: v=1,71 м/с</math>
  
−
Ответ: v=1,71 м/с</p>
 
  
−
<p> <br>
 
−
</p>
 
  
 
</div>
 
</div>
Строка 224: Строка 217:
  
  
−
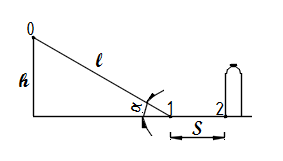
*Расчёт расстояния, который должен пройти мяч-2, чтобы скатиться с наклонной плоскости со скоростью v=0,069 м/с
+
*Расчёт расстояния, который должен пройти мяч-2, чтобы скатиться с наклонной плоскости со скоростью v=0,069 м/с (Вячеслав Красников)
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible-content">  
 
<div class="mw-collapsible-content">  
−
[[File:|thumb|]]
+
[[File:Расчёт_минимального_угла_наклона_плоскости,_при_котором_мяч-1_сможет_катиться.png]]
−
<p>Дано:</p>
+
<br><math>Дано:</math>
 +
 
 +
<br><math>v_0=0 м/с</math>
 +
<br><math>α=10°</math>
 +
<br><math>v=0,069 м/с</math>
 +
<br><math>μ=0,16</math>
  
−
<p>v_0=0 м/с<br>
+
<br><math>Найти: S</math>
−
α=10°<br>
 
−
v=0,069 м/с<br>
 
−
μ=0,16<br>
 
  
−
Найти: S<br>
+
<br><math>Решение: </math>
 +
<br><math>N+mg+μN=ma</math>
 +
<br><math>mgsinα-μmgcosα=m v^2/2S</math>
 +
<br><math>g(sinα-μcosα)=v^2/2S</math>
 +
<br><math>S=v^2/(2g(sinα-μcosα))</math>
 +
<br><math>S=((0,069)^2)/(2*10(0,17-0,16*0,98))=0,07м</math>
  
−
Решение: <br>
+
<br><math>Ответ: S=0,07м</math>
−
N+mg+μN=ma<br>
 
−
mgsinα-μmgcosα=m v^2/2S<br>
 
−
g(sinα-μcosα)=v^2/2S<br>
 
−
S=v^2/(2g(sinα-μcosα))<br>
 
−
S=((0,069)^2)/(2∙10(0,17-0,16∙0,98))=0,07м<br>
 
  
−
Ответ: S=0,07м</p><br>
 
−
<br>
 
  
  
Строка 252: Строка 245:
  
  
−
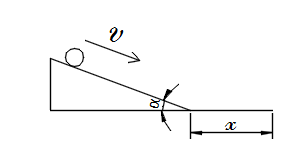
*Расчёт скорости, при которой мяч-2, брошенный под углом α=10°, пролетит 3см за 0,44с
+
*Расчёт скорости, при которой мяч-2, брошенный под углом α=10°, пролетит 3см за 0,44с (Кирилл Тихомиров)
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible-content">  
 
<div class="mw-collapsible-content">  
−
[[File:|thumb|]]
+
[[File:Расчёт_скорости.png ]]
−
<p>Дано:</p>
+
<br><math>Дано:</math>
 +
 
 +
<br><math>α=10°</math>
 +
<br><math>x=0,03 м </math>
 +
<br><math>t=0,44с</math>
  
−
<p>α=10°<br>
+
<br><math>Найти: v_0</math>
−
x=0,03 м <br>
 
−
t=0,44с<br>
 
  
−
Найти: v_0<br>
+
<br><math>Решение: </math>
 +
<br><math>x=v_0 cosα*t</math>
 +
<br><math>v_0=x/(t*cosα)</math>
 +
<br><math>v_0=0,03/(0,44*0,08)=0,069 м/с</math>
  
−
Решение: <br>
+
<br><math>Ответ: v_0=0,069 м/с</math>
−
x=v_0 cosα∙t<br>
 
−
v_0=x/(t∙cosα)<br>
 
−
v_0=0,03/(0,44∙0,08)=0,069 м/с<br>
 
  
−
Ответ: v_0=0,069 м/с</p>
 
  
−
<br>
 
−
<p></p>
 
  
  
Строка 279: Строка 271:
  
  
−
*Расчет импульса, который необходимо передать домино-3, чтобы оно упало
+
*Расчет импульса, который необходимо передать домино-3, чтобы оно упало(Анастасия Ханычкова)
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible-content">  
 
<div class="mw-collapsible-content">  
−
[[File:|thumb|]]
+
[[File:Расчёт_скорости,_с_которой_должен_катиться_мяч-1,_чтобы_сбить_стаканчики.png ]]
−
<p>Дано:</p>
+
<br><math>Дано:</math>
  
−
<p>m_мяча=0,0585 кг<br>
+
<br><math>m_мяча=0,0585 кг</math>
−
t=1c<br>
+
<br><math>t=1c</math>
  
−
Найти: p<br>
+
<br><math>Найти: p</math>
  
−
Решение:<br>
+
<br><math>Решение:</math>
−
p=F_взаим∙t<br>
+
<br><math>p=F_взаим*t</math>
−
F_взаим>F_домино=m_домино∙g<br>
+
<br><math>F_взаим>F_домино=m_домино∙g</math>
−
p_необ≥F_домино∙dt <br>
+
<br><math>p_необ≥F_домино*dt </math>
−
p_необ≥0,0585 кг∙м/с <br>
+
<br><math>p_необ≥0,0585 кг*м/с </math>
 +
 
 +
<br><math>Ответ: p_необ=0,0585 кг*м/с </math>
  
−
Ответ: p_необ=0,0585 кг∙м/с <br>
 
−
</p>
 
  
 
</div>
 
</div>
Строка 305: Строка 297:
  
  
−
*Расчет импульса, который домино-3 передает цилиндру при столкновении
+
*Расчет импульса, который домино-3 передает цилиндру при столкновении(Алёна Федотова)
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible-content">  
 
<div class="mw-collapsible-content">  
−
[[File:|thumb|]]
+
[[File:Расчёт_скорости,_с_которой_должен_катиться_мяч-1,_чтобы_сбить_стаканчики.png]]
−
<p>Дано:</p>
+
<br><math>Дано:</math>
  
−
<p>r=4,2см=0,042м<br>
+
<br><math>r=4,2см=0,042м</math>
−
m_ц=0,11кг<br>
+
<br><math>m_ц=0,11кг</math>
−
l=8см=0,08м<br>
+
<br><math>l=8см=0,08м</math>
−
p_домино=0,0585 кг∙м/с <br>
+
<br><math>p_домино=0,0585 кг*м/с </math>
  
−
Найти: p_цилиндра<br>
+
<br><math>Найти: p_цилиндра</math>
  
−
Решение:<br>
+
<br><math>Решение:</math>
−
sinα=r/l<br>
+
<br><math>sinα=r/l</math>
−
W_п1=m_д g l/2<br>
+
<br><math>W_п1=m_д g l/2</math>
−
W_k1=p^2/(2m_д )<br>
+
<br><math>W_k1=p^2/(2m_д )</math>
−
W_п2=m_д gh<br>
+
<br><math>W_п2=m_д gh</math>
−
h=l/2∙sinα=l/2∙r/l=r/2<br>
+
<br><math>h=l/2*sinα=l/2*r/l=r/2</math>
−
W_k2=(p_ц^2)/(2m_ц )=W_п1+W_k1-W_п2<br>
+
<br><math>W_k2=(p_ц^2)/(2m_ц )=W_п1+W_k1-W_п2</math>
−
(p_цил^2)/(2m_ц )=m_д g l/2+(p_д^2)/(2m_д )-m_д g r/2<br>
+
<br><math>(p_цил^2)/(2m_ц )=m_д g l/2+(p_д^2)/(2m_д )-m_д g r/2</math>
−
p_цил=2m_ц∙m_д g l/2+(P_д^2 m_д)/m_д -2m_ц m_д g r/2<br>
+
<br><math>p_цил=2m_ц*m_д g l/2+(P_д^2 m_д)/m_д -2m_ц m_д g r/2</math>
 +
 
 +
<br><math>Ответ: p_цил=0,065 кг*м/с </math>
  
−
Ответ: p_цил=0,065 кг∙м/с <br>
 
−
</p>
 
  
 
</div>
 
</div>
Строка 338: Строка 330:
  
  
−
*Расчёт импульса, который необходимо передать бутылке, чтобы она упала
+
*Расчёт импульса, который необходимо передать бутылке, чтобы она упала(Александра Асатиани)
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible-content">  
 
<div class="mw-collapsible-content">  
−
[[File:|thumb|]]
+
[[File:Расчёт_импульса,_который_необходимо_передать_бутылке,_чтобы_она_упала.png]]
−
<p>Дано:</p>
+
<br><math>Дано:</math>
  
−
<p>m_ц=0,11 кг<br>
+
<br><math>m_ц=0,11 кг</math>
−
m_б=0,013 кг<br>
+
<br><math>m_б=0,013 кг</math>
−
t=1,5 c<br>
+
мt=1,5 c</math>
  
−
Найти: p<br>
+
<br><math>Найти: p</math>
  
−
Решение:<br>
+
<br><math>Решение:</math>
−
p=F_вз∙t<br>
+
<br><math>p=F_вз∙t</math>
−
F_вз>F_(т.б)=m_б g=0,13H<br>
+
мF_вз>F_(т.б)=m_б g=0,13H</math>
−
p_цил=p=F_(т.б)∙dt=0,065 кг∙м/с <br>
+
<br><math>p_цил=p=F_(т.б)*dt=0,065 кг*м/с </math>
 +
 
 +
<br><math>Ответ: p=0,065 кг*м/с </math>
  
−
Ответ: p=0,065 кг∙м/с <br>
 
−
</p>
 
  
 
</div>
 
</div>
Строка 365: Строка 357:
  
  
−
*Найти длину наклонной плоскости, по которой катится цилиндр, чтобы он приобрёл скорость, необходимую для сбивания бутылки
+
*Найти длину наклонной плоскости, по которой катится цилиндр, чтобы он приобрёл скорость, необходимую для сбивания бутылки(Виталий Гончар)
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible-content">  
 
<div class="mw-collapsible-content">  
−
[[File:|thumb|]]
+
[[File:Найти_длину_наклонной_плоскости,_по_которой_катится_цилиндр,_чтобы_он_приобрёл_скорость,_необходимую_для_сбивания_бутылки.png]]
−
<p>Дано:</p>
+
<br><math>Дано:</math>
  
−
<p>α=30°<br>
+
<br><math>α=30°</math>
−
m_ц=0,11 кг<br>
+
<br><math>m_ц=0,11 кг</math>
−
m_б=0,013кг<br>
+
<br><math>m_б=0,013кг</math>
−
p_ц=0,065 кг∙м/с <br>
+
<br><math>p_ц=0,065 кг*м/с </math>
−
p_0=0,036 кг∙м/с <br>ъ\
+
<br><math>p_0=0,036 кг*м/с </math>
  
−
Найти: S<br>
+
<br><math>Найти: S</math>
  
−
Решение:<br>
+
<br><math>Решение:</math>
−
По ЗСЭ:<br>
+
<br><math>По ЗСЭ:</math>
−
m_ц gh+(p_0^2)/(2m_ц )=(p_ц^2)/(2m_б )<br>
+
<br><math>m_ц gh+(p_0^2)/(2m_ц )=(p_ц^2)/(2m_б )</math>
−
h=Ssinα<br>
+
<br><math>h=Ssinα</math>
−
m_ц gSsinα+(p_0^2)/(2m_ц )=p_ц/(2m_б )<br>
+
<br><math>m_ц gSsinα+(p_0^2)/(2m_ц )=p_ц/(2m_б )</math>
−
S=(p_ц^2 m_ц-p_0^2 m_б)/(2m_б m_ц^2 gsinα)=0,29м<br>
+
<br><math>S=(p_ц^2 m_ц-p_0^2 m_б)/(2m_б m_ц^2 gsinα)=0,29м</math>
 +
 
 +
<br><math>Ответ: S=0,29 м</math>
  
−
Ответ: S=0,29 м<br>
 
−
</p>
 
  
 
</div>
 
</div>
Строка 395: Строка 387:
  
  
−
*Рассчитать расстояние, которые пройдет цилиндр до бутылки (от наклонной плоскости)
+
*Рассчитать расстояние, которые пройдет цилиндр до бутылки (от наклонной плоскости)(Валентина Озерова)
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible-content">  
 
<div class="mw-collapsible-content">  
−
[[File:|thumb|]]
+
[[File:Рассчитать_расстояние,_которые_пройдет_цилиндр_до_бутылки_(от_наклонной_плоскости).png ]]
−
<p>Дано:</p>
+
<br><math>Дано:</math>
  
−
<p>α=30°<br>
+
<br><math>α=30°</math>
−
P_0=0,065 кг∙м/с <br>
+
<br><math>P_0=0,065 кг*м/с </math>
−
P_б=0,036 кг∙м/с <br>
+
<br><math>P_б=0,036 кг*м/с </math>
−
h= 0,145 м<br>
+
<br><math>h= 0,145 м</math>
−
l=0,29 м<br>
+
<br><math>l=0,29 м</math>
−
m=0,11кг<br>
+
<br><math>m=0,11кг</math>
−
t = 0,4 c<br>
+
<br><math>t = 0,4 c</math>
  
−
Найти: S<br>
+
<br><math>Найти: S</math>
  
−
Решение:<br>
+
<br><math>Решение:</math>
−
p_0=v_0 m_ц = > v_0=P_0/m_ц <br>
+
<br><math>p_0=v_0 m_ц = > v_0=P_0/m_ц </math>
−
v_2=p_б/m_ц <br>
+
<br><math>v_2=p_б/m_ц </math>
−
По ЗСЭ: E_n0+E_k0=E_k1<br>
+
<br><math>По ЗСЭ: E_n0+E_k0=E_k1</math>
−
m_ц gh+(m_ц v_0^2)/2=(m_ц v_1^2)/2<br>
+
<br><math> m_ц gh+(m_ц v_0^2)/2=(m_ц v_1^2)/2</math>
−
2gh+v_0^2=v_1^2<br>
+
<br><math> 2gh+v_0^2=v_1^2</math>
−
v_1=√(2gh+v_0^2 )=√(2gh+〖(p_0/m_ц )〗^2 )<br>
+
<br><math>v_1=√(2gh+v_0^2 )=√(2gh+〖(p_0/m_ц )〗^2 )</math>
−
|a|=|(v_2-v_1)/t|=|(p_б/m_ц -√(2gh〖(p_0/m_ц )〗^2 ))/t|; S=|(v_2^2-v_1^2)/2a|=t/2 (〖(p_б/m_ц )〗^2-2gh〖(p_0/m_ц )〗^2)/(p_б/m_ц -√(2gh+〖(p_0/m_ц )〗^2 ))<br>
+
<br><math>|a|=|(v_2-v_1)/t|=|(p_б/m_ц -√(2gh〖(p_0/m_ц )〗^2 ))/t|; S=|(v_2^2-v_1^2)/2a|=t/2 (〖(p_б/m_ц )〗^2-2gh〖(p_0/m_ц )〗^2)/(p_б/m_ц -√(2gh+〖(p_0/m_ц )〗^2 ))</math>
 +
 
 +
<br><math>Ответ: S=0,424м</math>
  
−
Ответ: S=0,424м<br>
 
−
</p>
 
  
 
</div>
 
</div>
Строка 429: Строка 421:
  
  
−
*Найти ускорение шара при скатывании с наклонной плоскости без скольжения
+
*Найти ускорение шара при скатывании с наклонной плоскости без скольжения(Дулма Соктоева)
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible-content">  
 
<div class="mw-collapsible-content">  
−
[[File:|thumb|]]
+
[[File:Найти_ускорение_шара_при_скатывании_с_наклонной_плоскости_без_скольжения.png ]]
−
<p>Дано:</p>
+
<br><math>Дано:</math>
  
−
<p>m=40∙10^(-3) кг<br>
+
<br><math>m=40*10^(-3) кг</math>
−
R=1,5∙10^(-2) м<br>
+
<br><math>R=1,5*10^(-2) м</math>
  
−
Найти: a<br>
+
<br><math>Найти: a</math>
  
−
Решение:<br>
+
<br><math>Решение:</math>
−
При скатывании тела с наклонной плоскости его потенциальная энергия переходит в кинетическую<br>
+
<br><math>При скатывании тела с наклонной плоскости его потенциальная энергия переходит в кинетическую</math>
−
mgh=(mv^2)/2+(Jω^2)/2 (1)<br>
+
<br><math>mgh=(mv^2)/2+(Jω^2)/2 (1)</math>
−
h=lsinα – подставим в (1)<br>
+
<br><math>h=lsinα – подставим в (1)</math>
−
ω=v/R – подставим в (1)<br>
+
<br><math>ω=v/R – подставим в (1)</math>
−
mglsinα=v^2/2 (m+J/R^2 )<br>
+
<br><math>mglsinα=v^2/2 (m+J/R^2 )</math>
−
l=(at^2)/2 – подставим в (1)<br>
+
<br><math>l=(at^2)/2 – подставим в (1)</math>
−
v=at – подставим в (1)<br>
+
<br><math>v=at – подставим в (1)</math>
−
mg (at^2)/2 sinα=(a^2 t^2)/2(m+J/R^2 )<br>
+
<br><math> mg (at^2)/2 sinα=(a^2 t^2)/2(m+J/R^2 )</math>
−
a=(m_д sinα)/(m+J⁄R^2 )<br>
+
<br><math>a=(m_д sinα)/(m+J⁄R^2 )</math>
−
J=2/5 mR^2 – момент инерции шара<br>
+
<br><math>J=2/5 mR^2 – момент инерции шара</math>
−
J=2/5∙40∙10^(-3)∙(1,5∙10^(-2) )^2=2/5∙40∙2,25∙10^(-7)=36∙10^(-7) кг∙м^2<br>
+
<br><math>J=2/5*40*10^(-3)*(1,5*10^(-2) )^2=2/5*40*2,25*10^(-7)=36*10^(-7) кг*м^2</math>
−
a=(40∙10^(-3)∙0,5∙9,8)/(40∙10^(-3)+16∙10^(-3) )=(196∙10^(-3))/(56∙10^(-3) )=3,5 м⁄с^2 </p>
+
<br><math>a=(40*10^(-3)*0,5*9,8)/(40*10^(-3)+16*10^(-3) )=(196*10^(-3))/(56*10^(-3) )=3,5 м⁄с^2 </math>
 +
 
 +
<br><math>Ответ: a=3,5 м⁄с^2 </math>
  
−
<p>Ответ: a=3,5 м⁄с^2 </p><br>
 
−
<br>
 
  
 
</div>
 
</div>
Строка 463: Строка 455:
  
  
−
*Расчёт импульса, который необходимо передать куску хлеба для его дальнейшего падения
+
*Расчёт импульса, который необходимо передать куску хлеба для его дальнейшего падения(Всеволод Макеев)
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible mw-collapsed">
 
<div class="mw-collapsible-content">  
 
<div class="mw-collapsible-content">  
−
[[File:|thumb|]]
+
[[File:Расчёт_импульса,_который_необходимо_передать_куску_хлеба_для_его_дальнейшего_падения.png]]
−
<p>Дано:</p>
+
<br><math>Дано:</math>
 +
 
 +
<br><math>l=25*10^(-2)</math>
 +
<br><math>a=3,5 м⁄с^2 </math>
  
−
<p>l=25∙10^(-2)<br>
+
<br><math>Найти: Р</math>
−
a=3,5 м⁄с^2 <br>
 
  
−
Найти: Р<br>
+
<br><math>Решение:</math>
 +
<br><math>l=v^2/2a=>v=√2al=√(2*3,5*25*10^(-2) )=√1,75=1,32 м⁄с</math>
 +
<br><math>P=40*10^(-3)*1,32=0,0528 (кг*м)/с</math>
  
−
Решение:<br>
+
<br><math>Ответ: Р=0,0528 кг*м/с</math>
−
l=v^2/2a=>v=√2al=√(2∙3,5∙25∙10^(-2) )=√1,75=1,32 м⁄с<br>
 
−
P=40∙10^(-3)∙1,32=0,0528 (кг∙м)/с<br>
 
  
−
Ответ: Р=0,0528 кг∙м/с</p><br>
 
−
<br>
 
  
 
</div>
 
</div>
Строка 487: Строка 479:
 
Машина Голдберга выполняет необходимую задачу: создает бутерброд с сыром. В процессе расчетов и пробных запусков пришлось убрать или модифицировать некоторые этапы. Вычисления немного подвели: пришлось исправлять высоту и длину некоторых конструкций. Возможно, если потестировать побольше, выявились бы еще несовершенства.
 
Машина Голдберга выполняет необходимую задачу: создает бутерброд с сыром. В процессе расчетов и пробных запусков пришлось убрать или модифицировать некоторые этапы. Вычисления немного подвели: пришлось исправлять высоту и длину некоторых конструкций. Возможно, если потестировать побольше, выявились бы еще несовершенства.
  
−
Видео запуска машины Голдберга.
+
Видео запуска машины Голдберга. https://www.youtube.com/watch?v=1B0-O_PYyVA
  
 
==Литература и ссылки==
 
==Литература и ссылки==

Текущая версия на 15:34, 17 июня 2019

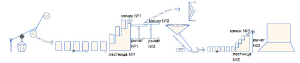
Машина Голдберга, машина Руба Голдберга, машина Робинсона-Голдберга, Машина Робинсона или заумная машина — это устройство, которое выполняет очень простое действие чрезвычайно сложным образом — как правило, посредством длинной последовательности взаимодействий по «принципу домино».


Описание[править]

Актуальность[править]

Актуальность данного проекта заключается в том, что при создании машины Голдберга можно найти практическое применение курсу теоретической механики и научиться использовать оборудование для цифрового производства DFKit. В частности 3D принтер и ЧПУ лазерный станок.

Цель проекта[править]

Создать машину Голдберга, которая будет выполнять цепочку взаимодействий, приводящих к созданию бутерброда с сыром

Задачи проекта[править]

  1. Определить последовательность действий, которые будут выполняться машиной Голдберга
  2. Подобрать необходимые материалы, предметы и инструменты для создания проекта
  3. Произвести расчеты и вычисления для определения параметров отдельных частей проекта
  4. Создать схему машины Голдберга
  5. Сделать отдельные части проекта
  6. Собрать машину Голдберга
  7. Произвести пробные запуски и устранить недочеты
  8. Смонтировать видео
  9. Произвести показательный запуск машины Голдберга
  10. Создать вики-страницу проекта

Проектная команда[править]

Группа 13151/3

  • Асатиани Александра
  • Башаро Егор
  • Гончар Виталий
  • Красников Вячеслав
  • Макеев Всеволод
  • Новикова Валентина
  • Озерова Надежда
  • Сигунова Алика
  • Соктоева Дулма
  • Тихомиров Кирилл
  • Ханычкова Анастасия
  • Федотова Алёна

Работа по проекту[править]

Действия, выполняемые машиной Голдберга[править]

Схема устройства машины Голдберга, запускающей видео на ноутбуке
  1. Математический маятник сбивает домино-1.
  2. Домино-1 сбивает последующие домино, создавая цепную реакцию.
  3. Последнее домино-2 падает и роняет подставку-1.
  4. В отсутствии подставки мяч-1 катится по наклонной плоскости.
  5. Шар-1 сбивает стаканчики.
  6. Привязанная тонкой нерастяжимой нитью поставка-2 падает.
  7. В отсутствии подставки-2 шар-2 катится по наклонной плоскости.
  8. Мяч-2 сбивает домино-3.
  9. Домино-3 падает и сбивает полый цилиндр без оснований.
  10. Цилиндр катится по наклонной плоскости и сбивает бутылку.
  11. Бутылка сбивает подставку-3, прикрепленную на невесомую нерастяжимую нить-2.
  12. Шар-3 в отсутствии опоры катится по наклонной плоскости.
  13. Шар-3 сбивает кусок хлеба.

Материалы и предметы для создания проекта[править]

  • мячики
  • фанера
  • клей
  • скотч
  • нитки
  • бутылка
  • картон
  • стаканчики пластиковые
  • пенопласт
  • губка посудомоечная
  • хлеб

Инструменты для создания проекта[править]

  • ЧПУ лазерный станок DFKit
  • Электроинструмент
  • Ручной инструмент

Этапы создания проекта[править]

Срок Задача Возникающие проблемы Что сделано к сроку
12.02.19 Определить последовательность действий машины Голдберга Каждый предлагает свои идеи. Возникли разногласия по некоторым пунктам. Определена основная последовательность.
26.02.19 Окончательно определить последовательность действий машины Голдберга Определена последовательность, сделан набросок действий.
12.03.19 Найти материалы для проекта Материалы было решено искать среди остатков от производства. Взяли все, что не жалко. Некоторые материалы купили в строительных магазинах. Необходимые материалы были найдены.
26.03.19 Найти предметы и инструменты для проекта В ФабЛабе есть все необходимые инструменты: ЧПУ лазерный станок DFKit, 3D принтер DFKit и т.д. Было найдено все необходимое.
09.04.19 Разбор этапов для расчетов Сложности в определении задачи в целом Начали решать проблему с расчетами.
23.04.19 Начало расчетов Возникли проблемы с решением задач. Определились до конца с расчетами. Разделили задания по группам.
07.05.19 Закончить расчеты Сложности в подведении итогов расчетов Решили все задачи, выполнили все расчеты.
10.05.19 Создать схему Понять, как лучше распределить этапы
14.05.19 Сделать рычаги, лестницы, домино, качающийся маятник Разделили работу по группам. Изучили, как работать с лазерным станком и 3D принтером, сделали с их помощью необходимые части проекта. Было сделано всё, что планировалось.
21.05.19 Сделать пробные запуски. Попытались несколько раз запустить машину. Устранили недочёты, выявленные на пробных запусках.
22.05.19 Монтирование видео. Презентация машины Голдберга Первая попытка запуска оказалась не совсем удачной, потому что слетел теннисный мячик с горки.
28.05.19 Создать вики-страницу проекта Отсутствие знаний о создании вики-страниц Результатом является данная страница

Расчеты элементов проекта[править]

  • Расчет расстояния и угла, на который необходимо отклонить маятник, чтобы он сбил домино(Надежда Новикова)

Расчет расстояния и угла, на который необходимо отклонить маятник, чтобы он сбил домино.png
[math]Дано:[/math]
[math]r_1=0,04м [/math]
[math]l=0,15м[/math]


[math]Найти:α,r[/math]


[math]Решение:[/math]
[math]r_1=lsinα_1[/math]
[math]α_1=arcsin⁡(r_1/l)[/math]
[math]α=3α_1=3 arcsin⁡〖(r_1/l)〗[/math]
[math]r=l(sin)_α=lsin⁡(3 arcsin⁡(r_1/l) )=0,15sin⁡(3 arcsin⁡(0,04/0,15) )=0,15sin⁡(3*15,466)=0,1086м[/math]
[math]α=3 arcsin⁡(0,02/0,07)=46,4°[/math]
[math]Ответ: r=0,1086м; α=46,4°[/math]


  • Расчёт минимального угла наклона плоскости, при котором мяч-1 сможет катиться (Алика Сигунова)

Расчёт минимального угла наклона плоскости, при котором мяч-1 сможет катиться.png
[math]Дано:[/math]
[math]m=0,0585кг[/math]
[math]l=0,2м[/math]
[math]g=10м/с^2[/math]
[math]V_0=0м/с[/math]
[math]V=1,71м/с[/math]


[math]Найти: α[/math]


[math]Решение:[/math]
[math]Из закона сохранения энергии:[/math]
[math]E_(k*1)+E_(n*1)=E_(k*2)+E_(n*2)[/math]
[math]E_k1=0; E_n2=0[/math]
[math]E_n1=E_k2[/math]
[math]E_n=mgh[/math]
[math]E_k=(mv^2)/2[/math]
[math]mgh=(mv^2)/2[/math]
[math]h=v^2/2g[/math]
[math]h=〖1,71〗^2/20=0,146м[/math]
[math]α=arcsin⁡(h/l)[/math]
[math]α=arcsin⁡(0,146/0,2)≈47°[/math]
[math]Ответ: α≈47°[/math]



  • Расчёт скорости, с которой должен катиться мяч-1, чтобы сбить стаканчики (Егор Башаро)

Расчёт минимального угла наклона плоскости, при котором мяч-1 сможет катиться.png
[math]Дано:[/math]


[math]m_мяча=0,0585кг[/math]
[math]m_(стак.)=0,01кг[/math]
[math]t=1c[/math]


[math]Найти: v[/math]


[math]Решение: [/math]
[math]p=F_взаим∙t[/math]
[math]F_взаим\gt F_(т.ст.)=m_ст*g=0,01*10=0,1H[/math]
[math]p_мяча=m_мяча*v[/math]
[math]v=P_м/m_м [/math]
[math]p_м=p=F_(т.стак)*dt[/math]
[math]v=(F_(т.ст)*dt)/m_мяча =(0,1 *1)/0,0585=1,71 м/с[/math]


[math]Ответ: v=1,71 м/с[/math]



  • Расчёт расстояния, который должен пройти мяч-2, чтобы скатиться с наклонной плоскости со скоростью v=0,069 м/с (Вячеслав Красников)

Расчёт минимального угла наклона плоскости, при котором мяч-1 сможет катиться.png
[math]Дано:[/math]


[math]v_0=0 м/с[/math]
[math]α=10°[/math]
[math]v=0,069 м/с[/math]
[math]μ=0,16[/math]


[math]Найти: S[/math]


[math]Решение: [/math]
[math]N+mg+μN=ma[/math]
[math]mgsinα-μmgcosα=m v^2/2S[/math]
[math]g(sinα-μcosα)=v^2/2S[/math]
[math]S=v^2/(2g(sinα-μcosα))[/math]
[math]S=((0,069)^2)/(2*10(0,17-0,16*0,98))=0,07м[/math]


[math]Ответ: S=0,07м[/math]



  • Расчёт скорости, при которой мяч-2, брошенный под углом α=10°, пролетит 3см за 0,44с (Кирилл Тихомиров)

Расчёт скорости.png
[math]Дано:[/math]


[math]α=10°[/math]
[math]x=0,03 м [/math]
[math]t=0,44с[/math]


[math]Найти: v_0[/math]


[math]Решение: [/math]
[math]x=v_0 cosα*t[/math]
[math]v_0=x/(t*cosα)[/math]
[math]v_0=0,03/(0,44*0,08)=0,069 м/с[/math]


[math]Ответ: v_0=0,069 м/с[/math]




  • Расчет импульса, который необходимо передать домино-3, чтобы оно упало(Анастасия Ханычкова)

Расчёт скорости, с которой должен катиться мяч-1, чтобы сбить стаканчики.png
[math]Дано:[/math]


[math]m_мяча=0,0585 кг[/math]
[math]t=1c[/math]


[math]Найти: p[/math]


[math]Решение:[/math]
[math]p=F_взаим*t[/math]
[math]F_взаим\gt F_домино=m_домино∙g[/math]
[math]p_необ≥F_домино*dt [/math]
[math]p_необ≥0,0585 кг*м/с [/math]


[math]Ответ: p_необ=0,0585 кг*м/с [/math]




  • Расчет импульса, который домино-3 передает цилиндру при столкновении(Алёна Федотова)

Расчёт скорости, с которой должен катиться мяч-1, чтобы сбить стаканчики.png
[math]Дано:[/math]


[math]r=4,2см=0,042м[/math]
[math]m_ц=0,11кг[/math]
[math]l=8см=0,08м[/math]
[math]p_домино=0,0585 кг*м/с [/math]


[math]Найти: p_цилиндра[/math]


[math]Решение:[/math]
[math]sinα=r/l[/math]
[math]W_п1=m_д g l/2[/math]
[math]W_k1=p^2/(2m_д )[/math]
[math]W_п2=m_д gh[/math]
[math]h=l/2*sinα=l/2*r/l=r/2[/math]
[math]W_k2=(p_ц^2)/(2m_ц )=W_п1+W_k1-W_п2[/math]
[math](p_цил^2)/(2m_ц )=m_д g l/2+(p_д^2)/(2m_д )-m_д g r/2[/math]
[math]p_цил=2m_ц*m_д g l/2+(P_д^2 m_д)/m_д -2m_ц m_д g r/2[/math]


[math]Ответ: p_цил=0,065 кг*м/с [/math]




  • Расчёт импульса, который необходимо передать бутылке, чтобы она упала(Александра Асатиани)

Расчёт импульса, который необходимо передать бутылке, чтобы она упала.png
[math]Дано:[/math]


[math]m_ц=0,11 кг[/math]
[math]m_б=0,013 кг[/math] мt=1,5 c</math>


[math]Найти: p[/math]


[math]Решение:[/math]
[math]p=F_вз∙t[/math] мF_вз>F_(т.б)=m_б g=0,13H</math>
[math]p_цил=p=F_(т.б)*dt=0,065 кг*м/с [/math]


[math]Ответ: p=0,065 кг*м/с [/math]




  • Найти длину наклонной плоскости, по которой катится цилиндр, чтобы он приобрёл скорость, необходимую для сбивания бутылки(Виталий Гончар)

Найти длину наклонной плоскости, по которой катится цилиндр, чтобы он приобрёл скорость, необходимую для сбивания бутылки.png
[math]Дано:[/math]


[math]α=30°[/math]
[math]m_ц=0,11 кг[/math]
[math]m_б=0,013кг[/math]
[math]p_ц=0,065 кг*м/с [/math]
[math]p_0=0,036 кг*м/с [/math]


[math]Найти: S[/math]


[math]Решение:[/math]
[math]По ЗСЭ:[/math]
[math]m_ц gh+(p_0^2)/(2m_ц )=(p_ц^2)/(2m_б )[/math]
[math]h=Ssinα[/math]
[math]m_ц gSsinα+(p_0^2)/(2m_ц )=p_ц/(2m_б )[/math]
[math]S=(p_ц^2 m_ц-p_0^2 m_б)/(2m_б m_ц^2 gsinα)=0,29м[/math]


[math]Ответ: S=0,29 м[/math]




  • Рассчитать расстояние, которые пройдет цилиндр до бутылки (от наклонной плоскости)(Валентина Озерова)

Рассчитать расстояние, которые пройдет цилиндр до бутылки (от наклонной плоскости).png
[math]Дано:[/math]


[math]α=30°[/math]
[math]P_0=0,065 кг*м/с [/math]
[math]P_б=0,036 кг*м/с [/math]
[math]h= 0,145 м[/math]
[math]l=0,29 м[/math]
[math]m=0,11кг[/math]
[math]t = 0,4 c[/math]


[math]Найти: S[/math]


[math]Решение:[/math]
[math]p_0=v_0 m_ц = \gt v_0=P_0/m_ц [/math]
[math]v_2=p_б/m_ц [/math]
[math]По ЗСЭ: E_n0+E_k0=E_k1[/math]
[math] m_ц gh+(m_ц v_0^2)/2=(m_ц v_1^2)/2[/math]
[math] 2gh+v_0^2=v_1^2[/math]
[math]v_1=√(2gh+v_0^2 )=√(2gh+〖(p_0/m_ц )〗^2 )[/math]
[math]|a|=|(v_2-v_1)/t|=|(p_б/m_ц -√(2gh〖(p_0/m_ц )〗^2 ))/t|; S=|(v_2^2-v_1^2)/2a|=t/2 (〖(p_б/m_ц )〗^2-2gh〖(p_0/m_ц )〗^2)/(p_б/m_ц -√(2gh+〖(p_0/m_ц )〗^2 ))[/math]


[math]Ответ: S=0,424м[/math]




  • Найти ускорение шара при скатывании с наклонной плоскости без скольжения(Дулма Соктоева)

Найти ускорение шара при скатывании с наклонной плоскости без скольжения.png
[math]Дано:[/math]


[math]m=40*10^(-3) кг[/math]
[math]R=1,5*10^(-2) м[/math]


[math]Найти: a[/math]


[math]Решение:[/math]
[math]При скатывании тела с наклонной плоскости его потенциальная энергия переходит в кинетическую[/math]
[math]mgh=(mv^2)/2+(Jω^2)/2 (1)[/math]
[math]h=lsinα – подставим в (1)[/math]
[math]ω=v/R – подставим в (1)[/math]
[math]mglsinα=v^2/2 (m+J/R^2 )[/math]
[math]l=(at^2)/2 – подставим в (1)[/math]
[math]v=at – подставим в (1)[/math]
[math] mg (at^2)/2 sinα=(a^2 t^2)/2(m+J/R^2 )[/math]
[math]a=(m_д sinα)/(m+J⁄R^2 )[/math]
[math]J=2/5 mR^2 – момент инерции шара[/math]
[math]J=2/5*40*10^(-3)*(1,5*10^(-2) )^2=2/5*40*2,25*10^(-7)=36*10^(-7) кг*м^2[/math]
[math]a=(40*10^(-3)*0,5*9,8)/(40*10^(-3)+16*10^(-3) )=(196*10^(-3))/(56*10^(-3) )=3,5 м⁄с^2 [/math]


[math]Ответ: a=3,5 м⁄с^2 [/math]




  • Расчёт импульса, который необходимо передать куску хлеба для его дальнейшего падения(Всеволод Макеев)

Расчёт импульса, который необходимо передать куску хлеба для его дальнейшего падения.png
[math]Дано:[/math]


[math]l=25*10^(-2)[/math]
[math]a=3,5 м⁄с^2 [/math]


[math]Найти: Р[/math]


[math]Решение:[/math]
[math]l=v^2/2a=\gt v=√2al=√(2*3,5*25*10^(-2) )=√1,75=1,32 м⁄с[/math]
[math]P=40*10^(-3)*1,32=0,0528 (кг*м)/с[/math]


[math]Ответ: Р=0,0528 кг*м/с[/math]


Результаты по проекту[править]

Машина Голдберга выполняет необходимую задачу: создает бутерброд с сыром. В процессе расчетов и пробных запусков пришлось убрать или модифицировать некоторые этапы. Вычисления немного подвели: пришлось исправлять высоту и длину некоторых конструкций. Возможно, если потестировать побольше, выявились бы еще несовершенства.

Видео запуска машины Голдберга. https://www.youtube.com/watch?v=1B0-O_PYyVA

Литература и ссылки[править]

  1. Инструкция по оказанию первой доврачебной помощи
  2. Инструкция по охране труда при работе с ручным инструментом
  3. Как создать машину Руба Голдберга самому
  4. Краткая теория по теоретической механике
  5. Машина Голдберга
  6. Методическое пособие по использованию ЧПУ лазерного станка DFKit
  7. Примеры различных машин Голдберга:
    75 Rube Goldberg Ideas & Inventions | DoodleChaos
    The Dresser - Rube Goldberg Machine for Getting Dressed | Joseph's Machines
    Marble run | Vivify cg
    Мастерская Голдберга | СПб и Мск | Лекториум
Источник — «http://tm.spbstu.ru/?title=Участник:MashinaG&oldid=53882»