Сравнение методов интегрирования уравнения гармонического осциллятора на python — различия между версиями
(Новая страница: « Курсовые работы 2018-2019 учебного года > '''Сравнение метод…») |
|||
| Строка 1: | Строка 1: | ||
| − | [[ Курсовые_работы_по_ВМДС:_2018-2019 | Курсовые работы 2018-2019 учебного года]] > '''Сравнение методов | + | [[ Курсовые_работы_по_ВМДС:_2018-2019 | Курсовые работы 2018-2019 учебного года]] > '''Сравнение методов решения уравнения гармонического осциллятора на python''' <HR> |
'''''Курсовой проект по [[Механика дискретных сред|Механике дискретных сред]]''''' | '''''Курсовой проект по [[Механика дискретных сред|Механике дискретных сред]]''''' | ||
Текущая версия на 13:32, 22 апреля 2019
Курсовые работы 2018-2019 учебного года > Сравнение методов решения уравнения гармонического осциллятора на pythonКурсовой проект по Механике дискретных сред
Исполнитель: Бальцер Анастасия
Группа: 43604/1
Семестр: осень 2018
Содержание
Постановка задачи[править]
Дано простейшее уравнение движения грузика на пружине: . Необходимо интегрировать его с помощью метода конечных разностей и средствами библиотеки scipy. Сравнить результаты интегрирования с аналитическим решением.
Решение[править]
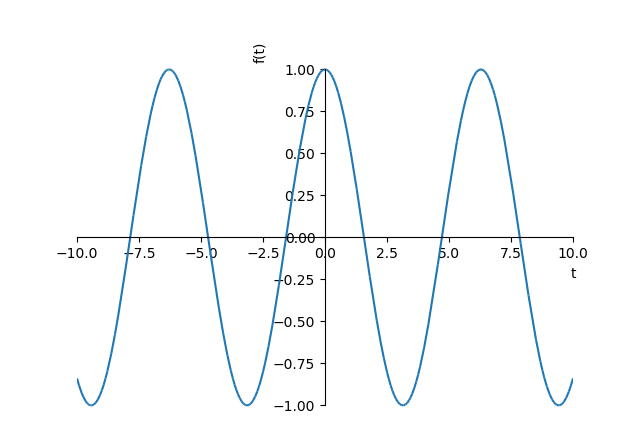
Рассмотрим уравнение модели гармонического осциллятора , где . Начальные условия , .
Аналитическое решение:
Найдем константы
Полное решение:
Построим график аналитического решения:
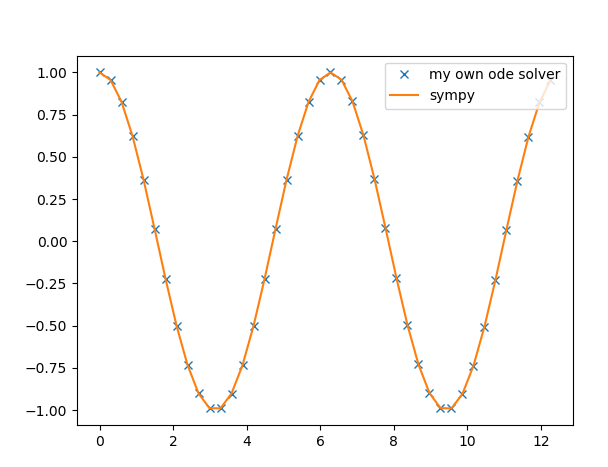
Численное решение методом конечных разностей:
То есть зная значения и находим значение на следующем шаге. находим из начальных условий.
Получаем решение (шаг по времени 0.001):
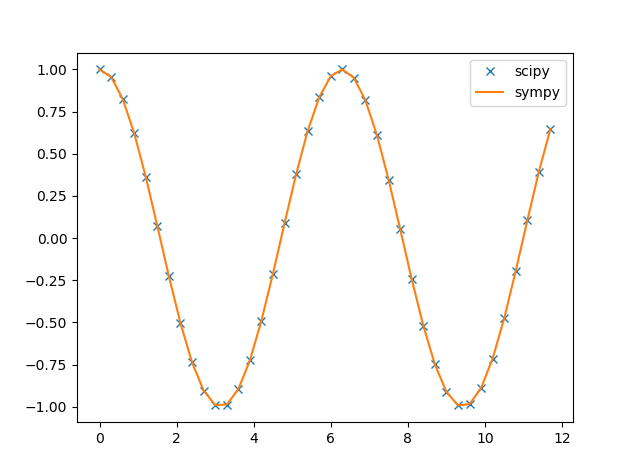
Численное решение с помощью библиотеки Scipy:
Будем решать систему ОДУ
Сравним полученное решение с аналитическим:
Выводы[править]
Таким образом, в ходе реализации данной работы можно сделать следующие выводы:
1. Если известно аналитическое решение, то лучше использовать его;
2. Реализация численных алгоритмов выполнима и в данной задаче показала высокую точность, однако в более сложных задачах это может быть более трудоемко;
3. Использование средств библиотеки scipy - быстрый и удобный способ решения задач, так как там уже реализовано множество численных методов. Для данной задачи оба численных решения показали высокую точность.