Переход к тепловому равновесию в гармонической ГЦК решетке — различия между версиями
(→Вывод уравнений) |
|||
| (не показано 18 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | '''Курсовой проект''' по [[Механика дискретных сред|Механике дискретных сред]] | |
| − | [ | + | '''Исполнитель:''' [http://tm.spbstu.ru/%D0%9B%D1%8F%D0%B6%D0%BA%D0%BE%D0%B2_%D0%A1%D0%B5%D1%80%D0%B3%D0%B5%D0%B9 Ляжков Сергей] |
| − | + | '''Группа:''' 43604/1 | |
| − | + | '''Семестр:''' осень 2018 | |
| − | =Результаты= | + | [[Файл: fcc.png|thumb|]] |
| + | |||
| + | ===Постановка задачи=== | ||
| + | |||
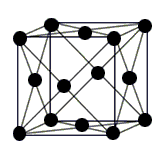
| + | Рассмотреть поведение кинетической температуры при переходе к тепловому равновесию в бесконечной гармонической гранецентрированной кубической (ГЦК) решетке при следующих начальных условиях: | ||
| + | |||
| + | # Частицы имеют нулевые перемещения. | ||
| + | # Частицы имеют случайные скорости. | ||
| + | # Распределение температуры - однородное. | ||
| + | # Кинетические температуры, соответствующие различным пространственным направлениям, не равны. | ||
| + | |||
| + | ===Вывод уравнений=== | ||
| + | |||
| + | Рассмотрим кристаллическую ГЦК решетку, состоящую из одинаковых частиц массой <math> m </math>, соединенных линейными пружинками жесткостью <math> c </math>. Уравнения движения частицы с радиус-вектором <math> \textbf{r} </math> имеют следующий вид: <br /> <math> m \ddot{\textbf{u}}(\textbf{r}) = \sum_\alpha \textbf{C}_\alpha \textbf{u}(\textbf{r}+\textbf{a}_\alpha)</math>, <br /> | ||
| + | где <math> \textbf{u}(\textbf{r}) = (u_x, u_y, u_z)^\top </math> - вектор-столбец, состоящий из компонент вектора перемещения частицы с радиус-вектором <math> \textbf{r} </math>, <math> \textbf{a}_\alpha </math> - векторы, соединяющие частицу с радиус-вектором <math> \textbf{r} </math> с ближайшими соседями. <math> \textbf{C}_\alpha </math> - матрицы, коэффициенты которых определяют вклад частицы номер <math> \alpha </math> в суммарную силу, действующую на частицу с радиус-вектором <math> \textbf{r} </math>. <math> \alpha = \pm 1...\pm 6 </math>, <math> \textbf{C}_\alpha = c\textbf{n}_\alpha \textbf{n}_\alpha</math>. <br /> | ||
| + | Векторы <math> \textbf{n}_\alpha = \frac{\textbf{a}_\alpha}{|\textbf{a}_\alpha|}</math> в ГЦК решетке имеют следующий вид: <br /> | ||
| + | <math> \textbf{n}_{\pm1}=\pm\frac{(\textbf{e}_x+\textbf{e}_y)}{\sqrt{2}}, \textbf{n}_{\pm4} = \pm(\textbf{n}_3-\textbf{n}_2) </math><br /> | ||
| + | <math> \textbf{n}_{\pm2}=\pm\frac{(\textbf{e}_y+\textbf{e}_z)}{\sqrt{2}}, \textbf{n}_{\pm5} = \pm(\textbf{n}_1-\textbf{n}_3) </math><br /> | ||
| + | <math> \textbf{n}_{\pm3}=\pm\frac{(\textbf{e}_x+\textbf{e}_z)}{\sqrt{2}}, \textbf{n}_{\pm6} = \pm(\textbf{n}_1-\textbf{n}_2) </math>, <br /> | ||
| + | где <math> \textbf{e}_x, \textbf{e}_y, \textbf{e}_z </math> - орты декартового базиса, направленные вдоль осей кубической симметрии. <br/> | ||
| + | Сделаем следующую подстановку в уравнения движения для получения дисперсионного соотношения <math> \omega </math>: <br /> | ||
| + | <math> \textbf{u}(\textbf{r}) = e^{\textrm{i}(\omega t + \textbf{k} \cdot \textbf{r})} </math>, | ||
| + | <br /> | ||
| + | где <math> \textbf{k} </math> - волновой вектор, и получим следующее уравнение: <br /> | ||
| + | <math> (\textbf{D}-\omega^2 \textbf{E})=0, \textbf{D} = -\frac{1}{m} \sum_\alpha \textbf{C}_\alpha e^{\textrm{i}{\textbf{k} \cdot \textbf{a}_\alpha}} </math>. <br/> | ||
| + | Таким образом, отыскание дисперсионного соотношения, необходимого для следующих формул, сводится к нахождению собственных чисел динамической матрицы <math> \textbf{D} </math>. <br/> Формула для для кинетической температуры <math> T </math>: <br/> | ||
| + | <math> T = \frac{T_0}{2} + B_1 + B_2 + B_3, \quad B_j = \int_\textbf{k} (\textrm{cos} (2\omega_j t)) \textrm{d} \textbf{k} </math>, <br /> | ||
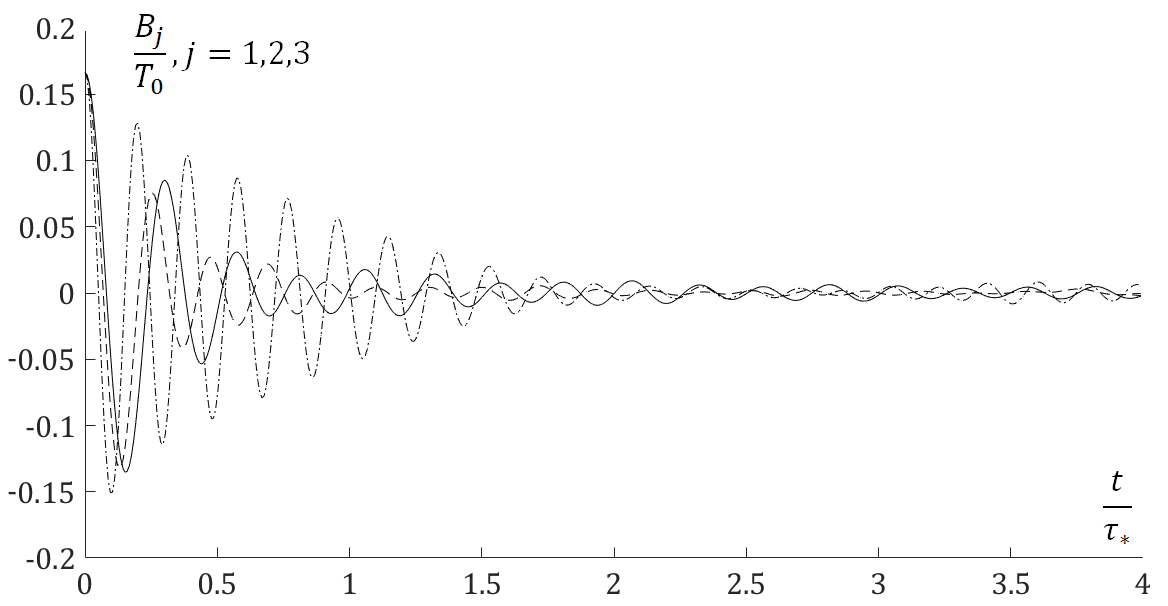
| + | где <math> T_0 </math> - начальное значение кинетической температуры. Величина <math> T </math> описывает колебания температуры, связанные с выравниванием кинетической и потенциальной энергий, величины <math> B_j </math> определяют вклад веток дисперсионного соотношения в эти колебания. <br /> | ||
| + | Рассмотрим бесконечное множество реализаций одного и того же кристалла. Кинетические температуры, соответствующие различным пространственным направлениям, в общем случае различаются. Следовательно, тепловое состояние описывается матричной температурой <math> \textbf{T}. </math> <br /> | ||
| + | <math> k_B \textbf{T} = m <\dot{\textbf{u}}(\textbf{r})\dot{\textbf{u}}(\textbf{r})^\top> </math>, <br /> | ||
| + | где <math> k_B </math> - постоянная Больцмана. <br /> | ||
| + | Поведение матричной температуры описывается следующей точной формулой: <br /> | ||
| + | <math> \textbf{T} = \int_\textbf{k} \textbf{P}\textbf{T}'\textbf{P}^\top, T'_{ij} = \frac{1}{2}(\textbf{P}^\top \textbf{T}_0 \textbf{P})_{ij}(\textrm{cos}((\omega_i+\omega_j)t)+\textrm{cos}((\omega_i-\omega_j)t)), </math> <br/> | ||
| + | где <math> \textbf{P} - </math> ортогональная матрица поляризации, составленная из единичных собственных векторов матрицы <math> \textbf{D} </math>, | ||
| + | <math> \textbf{T}_0 </math> - начальное значение матричной температуры. <br/> | ||
| + | Матричная и кинетическая температуры связаны следующим образом: <br/> | ||
| + | <math> T = \frac{1}{3}\textrm{tr}\textbf{T}. </math> | ||
| + | |||
| + | ===Результаты=== | ||
Вклады веток дисперсионного соотношения в колебания температуры: | Вклады веток дисперсионного соотношения в колебания температуры: | ||
| − | [[File:disp_stt.png]] | + | [[File:disp_stt.png|center]] |
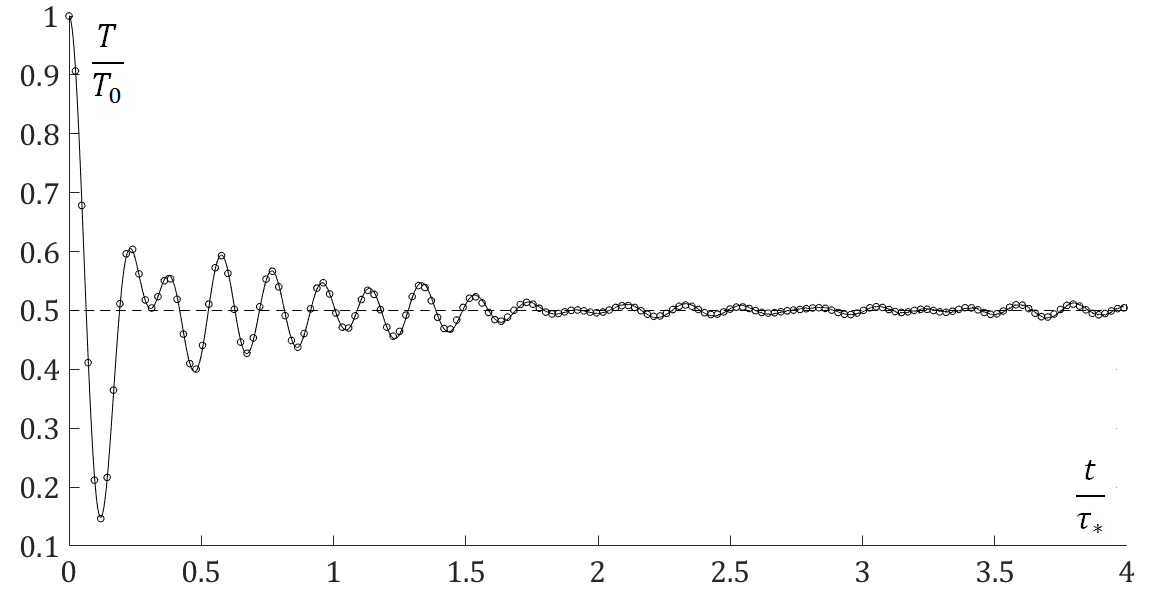
Колебания кинетической температуры, связанные с выравниванием кинетической и потенциальной энергий: | Колебания кинетической температуры, связанные с выравниванием кинетической и потенциальной энергий: | ||
| − | [[File:K_gck_ftt.png]] | + | [[File:K_gck_ftt.png|center]] |
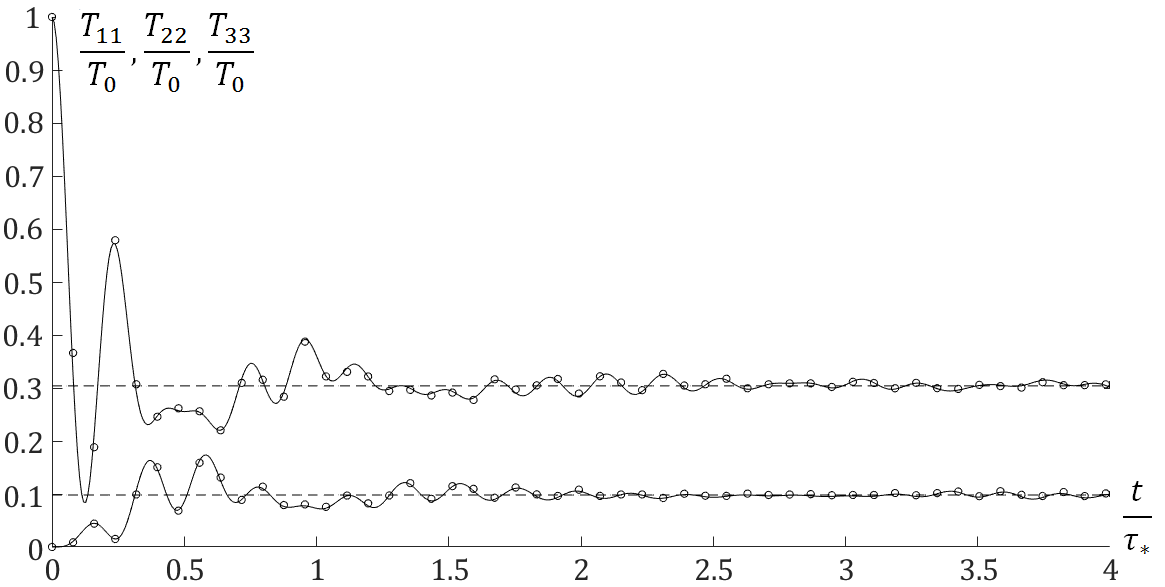
Перераспределение кинетической температуры по пространственным направлениям: | Перераспределение кинетической температуры по пространственным направлениям: | ||
| − | [[File:redistrib_ftt.png]] | + | [[File:redistrib_ftt.png|center]] |
| − | Линии - аналитическое решения по формулам, представленным в | + | Линии - аналитическое решения по формулам, представленным в нижеприведенной статье, точки - численное решение уравнения динамики решетки. |
| − | =Текст статьи= | + | ===Текст статьи=== |
[http://mech.spbstu.ru/File:FCC_stt.pdf Переход к тепловому равновесию в гармонической гранецентрированной кубической решетке] | [http://mech.spbstu.ru/File:FCC_stt.pdf Переход к тепловому равновесию в гармонической гранецентрированной кубической решетке] | ||
| − | =Неделя | + | ===Неделя науки 2018=== |
| + | |||
| + | Данный проект был представлен на конференции "Неделя науки 2018". | ||
[http://mech.spbstu.ru/File:Poster_NN.pdf Постер] | [http://mech.spbstu.ru/File:Poster_NN.pdf Постер] | ||
| + | |||
| + | ===См.также=== | ||
| + | |||
| + | [http://tm.spbstu.ru/%D0%9A%D1%83%D1%80%D1%81%D0%BE%D0%B2%D1%8B%D0%B5_%D1%80%D0%B0%D0%B1%D0%BE%D1%82%D1%8B_%D0%BF%D0%BE_%D0%92%D0%9C%D0%94%D0%A1:_2018-2019 Курсовые_работы_по_ВМДС:_2018-2019] | ||
Текущая версия на 18:48, 18 марта 2019
Курсовой проект по Механике дискретных сред
Исполнитель: Ляжков Сергей
Группа: 43604/1
Семестр: осень 2018
Содержание
Постановка задачи[править]
Рассмотреть поведение кинетической температуры при переходе к тепловому равновесию в бесконечной гармонической гранецентрированной кубической (ГЦК) решетке при следующих начальных условиях:
- Частицы имеют нулевые перемещения.
- Частицы имеют случайные скорости.
- Распределение температуры - однородное.
- Кинетические температуры, соответствующие различным пространственным направлениям, не равны.
Вывод уравнений[править]
Рассмотрим кристаллическую ГЦК решетку, состоящую из одинаковых частиц массой , соединенных линейными пружинками жесткостью . Уравнения движения частицы с радиус-вектором имеют следующий вид:
,
где - вектор-столбец, состоящий из компонент вектора перемещения частицы с радиус-вектором , - векторы, соединяющие частицу с радиус-вектором с ближайшими соседями. - матрицы, коэффициенты которых определяют вклад частицы номер в суммарную силу, действующую на частицу с радиус-вектором . , .
Векторы в ГЦК решетке имеют следующий вид:
,
где - орты декартового базиса, направленные вдоль осей кубической симметрии.
Сделаем следующую подстановку в уравнения движения для получения дисперсионного соотношения :
,
где - волновой вектор, и получим следующее уравнение:
.
Таким образом, отыскание дисперсионного соотношения, необходимого для следующих формул, сводится к нахождению собственных чисел динамической матрицы .
Формула для для кинетической температуры :
,
где - начальное значение кинетической температуры. Величина описывает колебания температуры, связанные с выравниванием кинетической и потенциальной энергий, величины определяют вклад веток дисперсионного соотношения в эти колебания.
Рассмотрим бесконечное множество реализаций одного и того же кристалла. Кинетические температуры, соответствующие различным пространственным направлениям, в общем случае различаются. Следовательно, тепловое состояние описывается матричной температурой
,
где - постоянная Больцмана.
Поведение матричной температуры описывается следующей точной формулой:
где ортогональная матрица поляризации, составленная из единичных собственных векторов матрицы ,
- начальное значение матричной температуры.
Матричная и кинетическая температуры связаны следующим образом:
Результаты[править]
Вклады веток дисперсионного соотношения в колебания температуры:
Колебания кинетической температуры, связанные с выравниванием кинетической и потенциальной энергий:
Перераспределение кинетической температуры по пространственным направлениям:
Линии - аналитическое решения по формулам, представленным в нижеприведенной статье, точки - численное решение уравнения динамики решетки.
Текст статьи[править]
Переход к тепловому равновесию в гармонической гранецентрированной кубической решетке
Неделя науки 2018[править]
Данный проект был представлен на конференции "Неделя науки 2018".