Переход к тепловому равновесию в гармонической ГЦК решетке — различия между версиями
(→Аннотация) |
(→top) |
||
| Строка 1: | Строка 1: | ||
| − | + | Курсовой проект по [[Механика дискретных сред|Механике дискретных сред]] | |
| − | [[Файл: fcc.png|thumb|]] | + | Исполнитель: [http://tm.spbstu.ru/%D0%9B%D1%8F%D0%B6%D0%BA%D0%BE%D0%B2_%D0%A1%D0%B5%D1%80%D0%B3%D0%B5%D0%B9 Ляжков Сергей] |
| + | |||
| + | Группа: 43604/1 | ||
| + | |||
| + | Семестр: осень 2018 | ||
| + | |||
| + | [[Файл: fcc.png|thumb|]] | ||
==Постановка задачи== | ==Постановка задачи== | ||
Версия 02:40, 22 января 2019
Курсовой проект по Механике дискретных сред
Исполнитель: Ляжков Сергей
Группа: 43604/1
Семестр: осень 2018
Постановка задачи
Рассмотреть поведение кинетической температуры при переходе к тепловому равновесию в бесконечной гармонической гранецентрированной кубической (ГЦК) решетке при следующих начальных условиях:
- Частицы имеют нулевые перемещения.
- Частицы имеют случайные скорости.
- Распределение температуры - однородное.
- Кинетические температуры, соответствующие различным пространственным направлениям, не равны.
Результаты
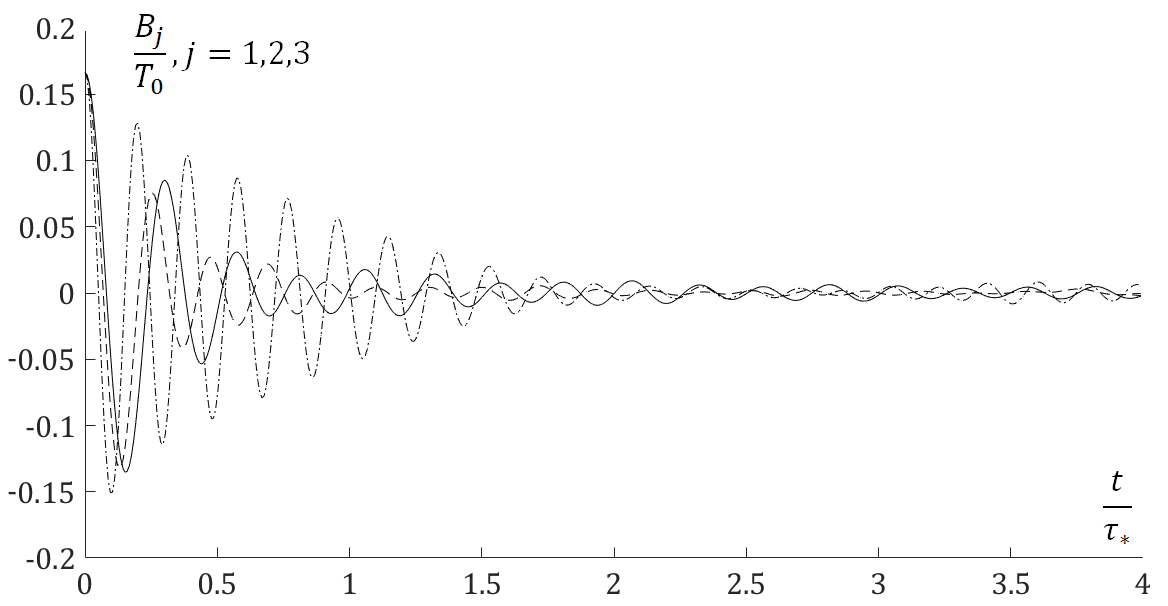
Вклады веток дисперсионного соотношения в колебания температуры:
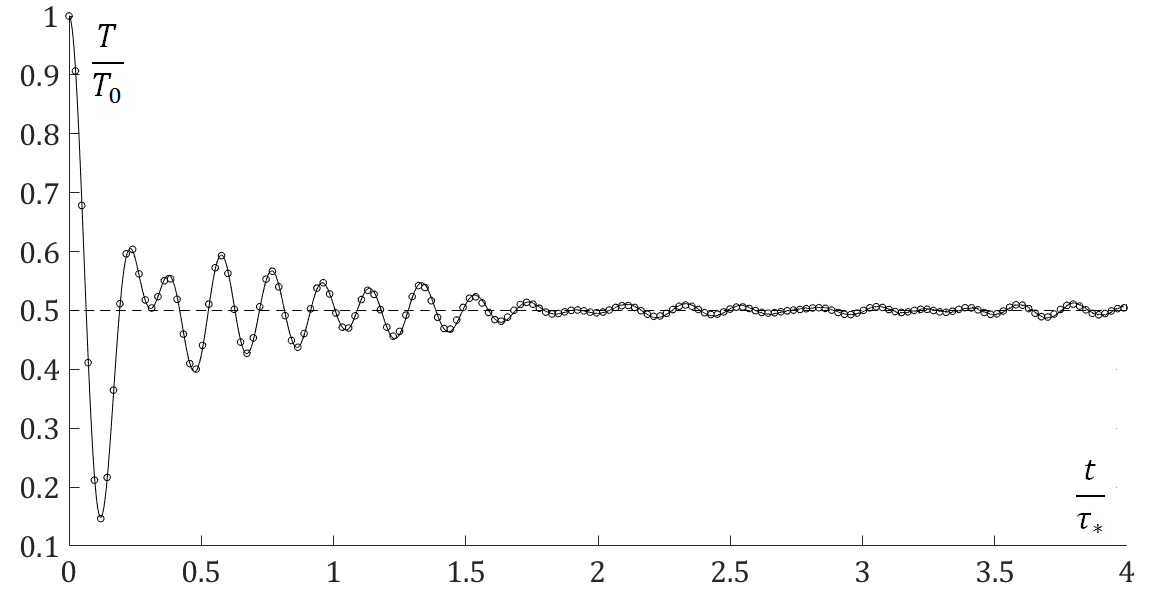
Колебания кинетической температуры, связанные с выравниванием кинетической и потенциальной энергий:
Перераспределение кинетической температуры по пространственным направлениям:
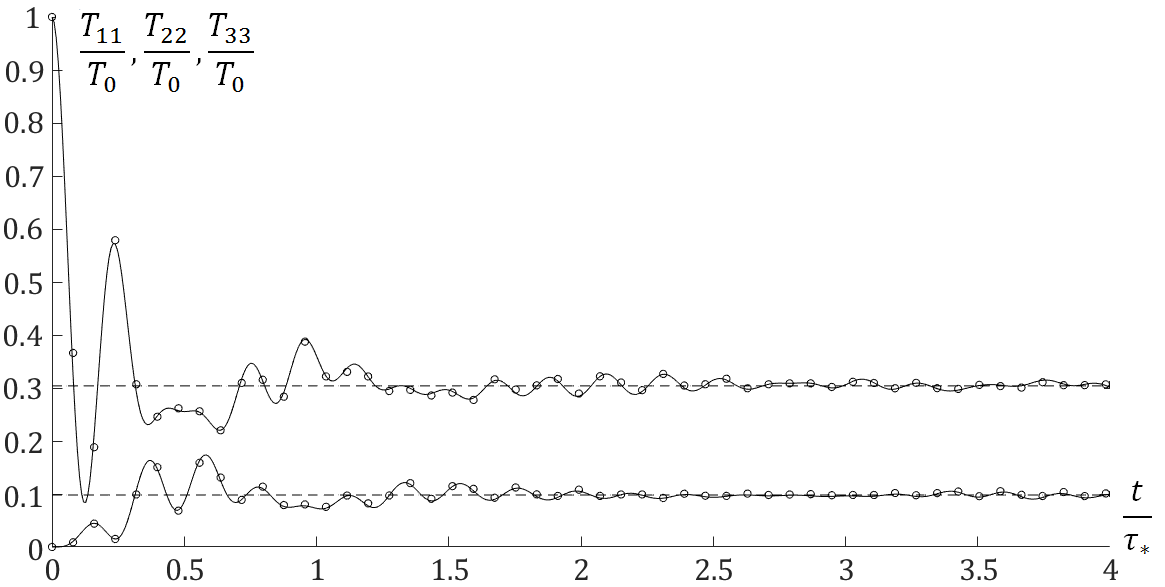
Линии - аналитическое решения по формулам, представленным в моей статье, точки - численное решение уравнения динамики решетки.
Текст статьи
Переход к тепловому равновесию в гармонической гранецентрированной кубической решетке