Перераспределение энергии по пространственным направлениям в кристаллах — различия между версиями
Meow (обсуждение | вклад) |
Meow (обсуждение | вклад) (→Заключение) |
||
| (не показано 20 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
'''''Выпускная квалификационная работа''''' | '''''Выпускная квалификационная работа''''' | ||
| + | |||
| + | '''Направление:''' 01.03.03 – «Механика и математическое моделирование» | ||
'''Выполнил:''' студент группы 43604/1 [[Шварёв Николай|Н.Г. Шварёв]] | '''Выполнил:''' студент группы 43604/1 [[Шварёв Николай|Н.Г. Шварёв]] | ||
| Строка 5: | Строка 7: | ||
'''Руководитель:''' кандидат физ.-мат. наук, доцент кафедры [[Теоретическая механика]] [[Виталий Кузькин|В.А. Кузькин]] | '''Руководитель:''' кандидат физ.-мат. наук, доцент кафедры [[Теоретическая механика]] [[Виталий Кузькин|В.А. Кузькин]] | ||
| + | Материалы: | ||
| + | * [[Медиа: Шварёв Н.Г._edited_3.pdf|диплом]] | ||
| + | * [[Медиа: PosterMeow.pdf|постер]] | ||
| + | * [[Медиа: ЗащитаMeow.pdf|презентация]] | ||
==Введение== | ==Введение== | ||
| Строка 28: | Строка 34: | ||
Из-за того, что температура прямо пропорциональна кинетической энергии, а в дальнейшем будет происходить рассмотрение только обезразмеренного значения температуры, то понятия температуры и кинетической энергии будут равносильны: <math> T_{xx} = E_x, T_{yy} = E_y </math> | Из-за того, что температура прямо пропорциональна кинетической энергии, а в дальнейшем будет происходить рассмотрение только обезразмеренного значения температуры, то понятия температуры и кинетической энергии будут равносильны: <math> T_{xx} = E_x, T_{yy} = E_y </math> | ||
| + | |||
| + | Для уменьшения влияния случайных начальных условий проводится усреднение по реализациям кристалла. | ||
| Строка 35: | Строка 43: | ||
• рассмотрение процесса выравнивания температур; | • рассмотрение процесса выравнивания температур; | ||
| + | |||
• рассмотрение влияния нелинейности на поведение системы; | • рассмотрение влияния нелинейности на поведение системы; | ||
| + | |||
• выделение медленного процесса, вызываемого нелинейностью; | • выделение медленного процесса, вызываемого нелинейностью; | ||
| − | • определение формы выделенного медленного процесса | + | |
| + | • определение формы выделенного медленного процесса. | ||
| + | |||
| + | |||
| + | ==Модель двумерного кристалла== | ||
| + | |||
| + | [[File:Triangular_lattice_10x10.png|thumbnail|Рис.1. Пример треугольной кристаллической решетки 10x10, получаемый в результате работы программы]] | ||
| + | |||
| + | • Рассматривается [[Треугольная кристаллическая решетка]]. | ||
| + | |||
| + | • Для взаимодействия между частицами используется [[Потенциал Леннард-Джонса]]. | ||
| + | |||
| + | • Задаются следующие начальные условия: | ||
| + | |||
| + | <math>v_x ≤ v_{max}, v_y = 0, u_x = 0, u_y = 0</math>. | ||
| + | |||
| + | В начальный момент времени рассматриваются случайные начальные скорости вдоль одной оси (оси X), ограниченные некоторым варьируемым максимальным значением <math>v_{max}</math>, нулевые начальные скорости вдоль другой оси (оси Y) и нулевые перемещения вдоль обеих осей. | ||
| + | |||
| + | • Используются периодические граничные условия Борна-Кармана. | ||
| + | |||
| + | |||
| + | ==Выравнивание температуры== | ||
| + | |||
| + | |||
| + | <gallery widths=400px heights=300px perrow = 1> | ||
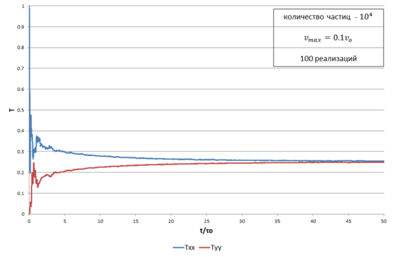
| + | Файл:Temperature equalization.png|Рис.2. Поведение кинетической температуры при усреднении по 100 реализациям | ||
| + | </gallery> | ||
| + | |||
| + | Как можно заметить, оба графика стремятся к асимптоте T = ¼ . Это связано с тем, что со временем при переходе к стационарному состоянию кинетическая и потенциальная энергия выравниваются, значит, половина кинетической энергии уходит в потенциальную. А при наличии нелинейности разность <math>T_{xx}-T_{yy}</math> стремится к нулю, следовательно, половина от оставшейся половины уходит на равное распределение по пространственным направлениям. | ||
| + | |||
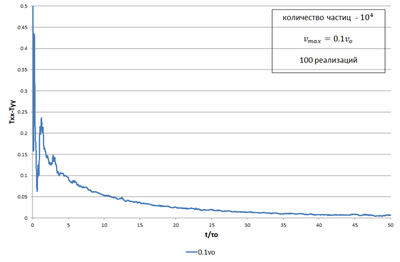
| + | На начальном интервале в несколько периодов <math>τ_o</math> происходит перераспределение кинетической и потенциальной энергии, а далее – перераспределение кинетической энергии по пространственным направлениям. | ||
| + | |||
| + | |||
| + | <gallery widths=400px heights=300px perrow = 1> | ||
| + | Файл:Redistribution_of_energy.png|Рис.3. График перераспределения кинетической температуры по направлениям | ||
| + | </gallery> | ||
| + | |||
| + | |||
| + | ==Степень влияния нелинейности== | ||
| + | |||
| + | Далее посмотрим, как, варьируя амплитуду начальных скоростей, а, следовательно, вместе с ней и температуру, можно изменять степень влияния нелинейности на поведение системы. | ||
| + | |||
| + | |||
| + | <gallery widths=400px heights=300px perrow = 1> | ||
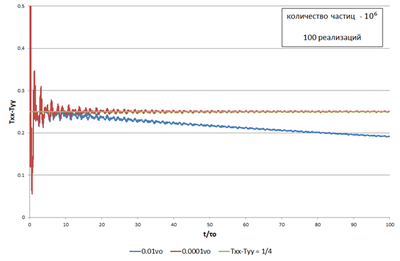
| + | Файл:Influence_of_nonlinearity.png|Рис.4. Степень влияния нелинейности | ||
| + | </gallery> | ||
| + | |||
| + | Видно, что скорость <math>0.0001v_o</math> настолько мала, что переходный тепловой процесс в кристалле Леннард-Джонса с такой скоростью хорошо описывается гармонической моделью и формулой, выведенной в работе [1], при стремлении к стационарному состоянию: | ||
| + | <math>\widehat T_{xx}-\widehat T_{yy}=\frac{1}{4}(\widehat T_{xx}^o-\widehat T_{yy}^o)</math>, | ||
| + | |||
| + | а при скорости <math>0.01v_o</math> разность <math>T_{xx}-T_{yy}</math> уменьшается в 4 раза, после чего достаточно медленно стремится к нулю. | ||
| + | |||
| + | |||
| + | ==Вывод формулы подобия== | ||
| + | |||
| + | Рассмотрим несколько расчетов с разными начальным скоростями. | ||
| + | |||
| + | <gallery widths=450px heights=300px perrow = 1> | ||
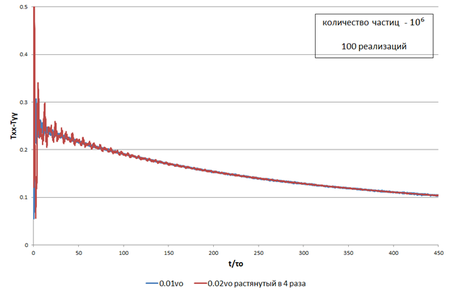
| + | Файл:Stretched_0.02.png|Рис.5. <math>0.01v_o</math> и <math>0.02v_o</math>, растянутый в 4 раза вдоль горизонтальной оси | ||
| + | </gallery> | ||
| + | |||
| + | <gallery widths=450px heights=300px perrow = 1> | ||
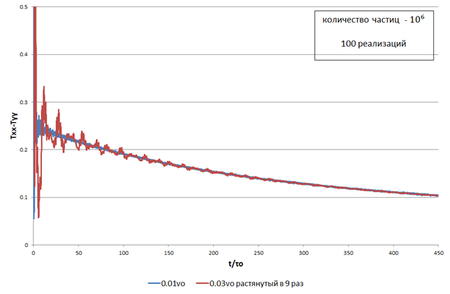
| + | Файл:Stretched_0.03.png|Рис.6. <math>0.01v_o</math> и <math>0.03v_o</math>, растянутый в 9 раз вдоль горизонтальной оси | ||
| + | </gallery> | ||
| + | |||
| + | <gallery widths=450px heights=300px perrow = 1> | ||
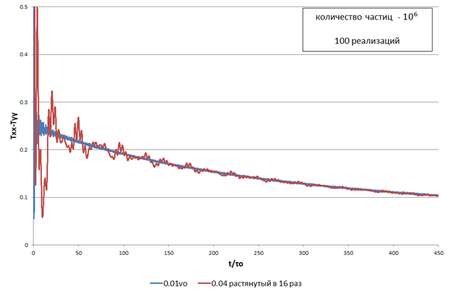
| + | Файл:Stretched_0.04.png|Рис.7. <math>0.01v_o</math> и <math>0.04v_o</math>, растянутый в 16 раз вдоль горизонтальной оси | ||
| + | </gallery> | ||
| + | |||
| + | <gallery widths=450px heights=300px perrow = 1> | ||
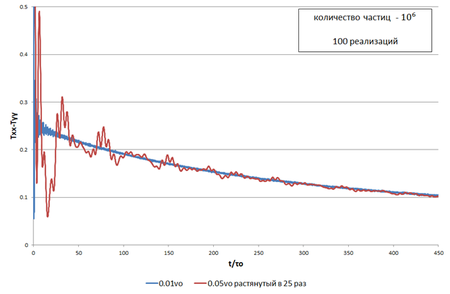
| + | Файл:Stretched_0.05.png|Рис.8. <math>0.01v_o</math> и <math>0.05v_o</math>, растянутый в 25 раз вдоль горизонтальной оси | ||
| + | </gallery> | ||
| + | |||
| + | Видно, что спустя некоторое время происходит полное совмещение графиков. Оценим это время: | ||
| + | <math> t ≥ 10 τ_o (\frac{v_{max2}}{v_{max1}})^2 </math>, | ||
| + | |||
| + | где <math> v_{max2} > v_{max1} </math>. | ||
| + | |||
| + | |||
| + | Таким образом, получаем формулу подобия для различных амплитуд начальных скоростей и оценку её области применимости: | ||
| + | |||
| + | <math>∆T_1(t)=∆T_2(t (\frac{v_{max2}}{v_{max1}})^2) </math>, | ||
| + | |||
| + | <math>t ≥ 10 τ_o </math>, | ||
| + | |||
| + | где за <math> ∆T</math> принята разность <math>T_{xx}-T_{yy}</math> | ||
| + | |||
| + | ==Выделение медленного процесса== | ||
| + | |||
| + | |||
| + | ==Заключение== | ||
| + | |||
| + | |||
| + | |||
| + | Автор благодарен [[Старобинский Егор|Е.Б. Старобинскому]] за полезные обсуждения. | ||
| + | |||
| + | ==Список литературы== | ||
Текущая версия на 20:20, 7 февраля 2018
Выпускная квалификационная работа
Направление: 01.03.03 – «Механика и математическое моделирование»
Выполнил: студент группы 43604/1 Н.Г. Шварёв
Руководитель: кандидат физ.-мат. наук, доцент кафедры Теоретическая механика В.А. Кузькин
Материалы:
Содержание
Введение[править]
Количественное описание неравновесных тепловых процессов в кристаллах – одна из актуальных проблем современной физики. Это связано со стремительным развитием нанотехнологий. В связи с этим большой интерес представляют процессы, происходящие в твердых телах при переходе к состоянию термодинамического равновесия. Неравновесное состояние может быть вызвано, к примеру, прохождением ударных волн или быстрым лазерным воздействием. Тогда кинетические энергии теплового движения атомов в разных направлениях могут значительно различаться. Это, в свою очередь, показывает, что кинетическая температура может проявлять тензорные свойства. На фронте ударной волны, распространяющейся вдоль одной из осей, например, оси X, выполняются следующее соотношение:
,
где - кинетические температуры вдоль соответствующих направлений, - постоянная Больцмана.
При переходе к равновесному состоянию в кристалле реализуется два процесса:
1)Выравнивание кинетической и потенциальной энергий;
2)Перераспределение кинетической энергии по пространственным направлениям.
Данная работа посвящена численному описанию перераспределения кинетической энергии по пространственным направлениям в негармонических кристаллах с треугольной кристаллической решеткой.
Далее будет рассматриваться обезразмеренное значение температуры: ,
где - значения в начальный момент времени соответственно
Из-за того, что температура прямо пропорциональна кинетической энергии, а в дальнейшем будет происходить рассмотрение только обезразмеренного значения температуры, то понятия температуры и кинетической энергии будут равносильны:
Для уменьшения влияния случайных начальных условий проводится усреднение по реализациям кристалла.
Цели и задачи работы[править]
Целью данной работы является проведение компьютерного моделирования перераспределения кинетической по пространственным направлениям в негармонических кристаллах с треугольной кристаллической решеткой. В связи с поставленной целью решаются следующие задачи:
• рассмотрение процесса выравнивания температур;
• рассмотрение влияния нелинейности на поведение системы;
• выделение медленного процесса, вызываемого нелинейностью;
• определение формы выделенного медленного процесса.
Модель двумерного кристалла[править]
• Рассматривается Треугольная кристаллическая решетка.
• Для взаимодействия между частицами используется Потенциал Леннард-Джонса.
• Задаются следующие начальные условия:
.
В начальный момент времени рассматриваются случайные начальные скорости вдоль одной оси (оси X), ограниченные некоторым варьируемым максимальным значением , нулевые начальные скорости вдоль другой оси (оси Y) и нулевые перемещения вдоль обеих осей.
• Используются периодические граничные условия Борна-Кармана.
Выравнивание температуры[править]
Как можно заметить, оба графика стремятся к асимптоте T = ¼ . Это связано с тем, что со временем при переходе к стационарному состоянию кинетическая и потенциальная энергия выравниваются, значит, половина кинетической энергии уходит в потенциальную. А при наличии нелинейности разность стремится к нулю, следовательно, половина от оставшейся половины уходит на равное распределение по пространственным направлениям.
На начальном интервале в несколько периодов происходит перераспределение кинетической и потенциальной энергии, а далее – перераспределение кинетической энергии по пространственным направлениям.
Степень влияния нелинейности[править]
Далее посмотрим, как, варьируя амплитуду начальных скоростей, а, следовательно, вместе с ней и температуру, можно изменять степень влияния нелинейности на поведение системы.
Видно, что скорость настолько мала, что переходный тепловой процесс в кристалле Леннард-Джонса с такой скоростью хорошо описывается гармонической моделью и формулой, выведенной в работе [1], при стремлении к стационарному состоянию: ,
а при скорости разность уменьшается в 4 раза, после чего достаточно медленно стремится к нулю.
Вывод формулы подобия[править]
Рассмотрим несколько расчетов с разными начальным скоростями.
Видно, что спустя некоторое время происходит полное совмещение графиков. Оценим это время: ,
где .
Таким образом, получаем формулу подобия для различных амплитуд начальных скоростей и оценку её области применимости:
,
,
где за принята разность
Выделение медленного процесса[править]
Заключение[править]
Автор благодарен Е.Б. Старобинскому за полезные обсуждения.