Мещерский 48.30 — различия между версиями

Версия 04:14, 4 февраля 2018

Задача 48.30 из сборника задач Мещерского : составить уравнения движения стержня и смоделировать систему на языке программирования JavaScript.

Формулировка задачи

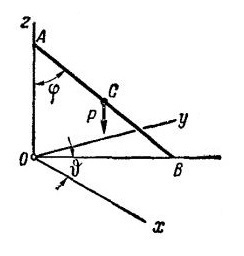
Однородный тонкий стержень АВ весом Р и длиной [math]2l[/math] скользит концом А по вертикальной прямой, а концом В по по горизонтальной плоскости. Составить уравнения движения стержня.

Реализация на языке JavaScript

Используемые библиотеки

• three.js
• stats.min.js
• dat.gui.min.js
• jquery-1.9.0.js

Решение задачи

Используем уравнение Лагранжа 2-го рода:

[math]\frac{d}{dt}\left(\frac{\partial L}{\partial\dot q_i}\right) - \frac{\partial L}{\partial q_i} = 0 , (i = 1,2)[/math] , где

L = T - П - функция Лагранжа
T - кинетическая энергия системы
П - потенциальная энергия системы
q - независимые обобщенные координаты

Решая задачу, получим следующие уравнения движения:

[math]ddot φ -dot ø^{2} sinφ cosφ = \frac{3g}{4l}sinφ)[/math]

[math]\ddot ø sin^{2}φ + 2dot ødot φsinφcosφ[/math],

где v0 - начальная скорость тела 1

См. также

• Задачи по теоретической механике