Моделирование провисания троса под действием силы тяжести — различия между версиями
Kozulski (обсуждение | вклад) |
Kozulski (обсуждение | вклад) |
||
| Строка 14: | Строка 14: | ||
== Моделирование == | == Моделирование == | ||
| − | Трос провисает под действием силы тяжести и течения. В данной модели учитывается только сила тяжести. Трос моделируется как набор грузов, связанных линейными и угловыми пружинами. Концы троса закреплены. Линейные пружины подчиняются закону Гука: <math>F = k \Delta l | + | Трос провисает под действием силы тяжести и течения. В данной модели учитывается только сила тяжести. Трос моделируется как набор грузов, связанных линейными и угловыми пружинами. Концы троса закреплены. Линейные пружины подчиняются закону Гука: |
| + | <math>F = k \Delta l</math>, | ||
| + | а угловые создают момент <math>M = C(\phi - \Pi).</math>. | ||
Версия 14:08, 26 января 2018
Курсовой проект по Механике дискретных сред
Исполнитель: Логинов Александр
Группа: 10 (43604/1)
Семестр: осень 2017
Введение
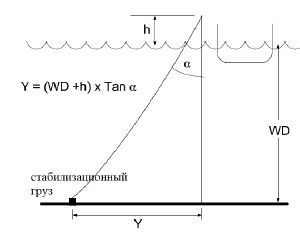
Данная задача о провисании троса возникла из судостроительной отрасли. При навигации судов при помощи системы динамического позиционирования необходимо знать местоположение судна (подробнее о системе ДП в этой и этой презентациях). Одним из датчиков, позволяющих определить относительную позицию судна, является taut wire. Конструкционно представляет собой кран-балку, установленную на судне, через которую перекинут трос, закрепленный на дне при помощи тяжелого груза. Измеряя угол отклонения троса у конца кран-балки от вертикали, система определяет смещение судна от заданной позиции. Отклонение формы троса от прямой оказывает сильное влияние на точность позиционирования.
Моделирование
Трос провисает под действием силы тяжести и течения. В данной модели учитывается только сила тяжести. Трос моделируется как набор грузов, связанных линейными и угловыми пружинами. Концы троса закреплены. Линейные пружины подчиняются закону Гука: , а угловые создают момент .