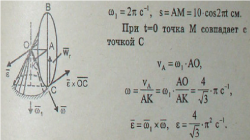Мещерский 25.18 — различия между версиями
Материал из Department of Theoretical and Applied Mechanics
| (не показано 5 промежуточных версий этого же участника) | |||
| Строка 10: | Строка 10: | ||
*dat.gui.js | *dat.gui.js | ||
| − | == | + | == Условия задачи == |
| − | |||
| − | [[File:25.18.png|thumb|right|Картинка к задаче.]] | + | [[File:25.18.png|250px|thumb|right|Картинка к задаче.]] |
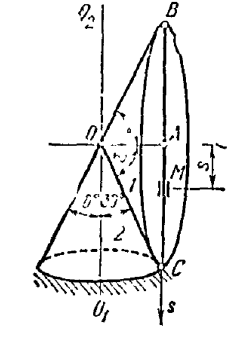
Круговой конус <math>1</math> с углом при вершине равным <math> \varphi </math> прикреплён к неподвижному конусу <math>2</math> с углом при вершине равным <math>180 - \varphi </math> шарниром <math>O</math> и катится без скольжения. При этом ось <math>O A</math> конуса <math>1</math> совершает вокруг вертикальной оси <math>O_1 O_2</math> один оборот в секунду. Вдоль диаметра <math>B C = 20 см</math> основания конуса <math>1</math> проложена направляющая, по которой скользит ползун <math>M</math>, совершая колебания около центра <math>А</math> по закону <math>s=AM=10cos2\pi t</math>. В начальный момент времени <math>t = 0</math> направляющая <math>В С</math> в одной вертикальной плоскости с шарниром <math>O</math>. Найти модуль абсолютного ускорения ползунка <math>M</math> в момент <math>t = 0</math>. | Круговой конус <math>1</math> с углом при вершине равным <math> \varphi </math> прикреплён к неподвижному конусу <math>2</math> с углом при вершине равным <math>180 - \varphi </math> шарниром <math>O</math> и катится без скольжения. При этом ось <math>O A</math> конуса <math>1</math> совершает вокруг вертикальной оси <math>O_1 O_2</math> один оборот в секунду. Вдоль диаметра <math>B C = 20 см</math> основания конуса <math>1</math> проложена направляющая, по которой скользит ползун <math>M</math>, совершая колебания около центра <math>А</math> по закону <math>s=AM=10cos2\pi t</math>. В начальный момент времени <math>t = 0</math> направляющая <math>В С</math> в одной вертикальной плоскости с шарниром <math>O</math>. Найти модуль абсолютного ускорения ползунка <math>M</math> в момент <math>t = 0</math>. | ||
| − | |||
| − | [[File:Solve1 25.18.png| | + | == Решение == |
| + | |||
| + | [[File:Solve1 25.18.png|250px|thumb|left|]] | ||
| + | |||
| + | <math> ω_1 = 2\pi c </math>, <math> s = AM = 10cos2\pi t </math> см. При <math> t = 0 </math> точка <math> M </math> совпадает с точкой <math> C </math> | ||
| + | |||
| + | <math> V_a = ω_1 AO </math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| − | |||
== См. также == | == См. также == | ||
| − | + | [[Проектная деятельность по информатике]] | |
| − | + | [[Задачи по теоретической механике]] | |
[[Category: Студенческие проекты]] | [[Category: Студенческие проекты]] | ||
Текущая версия на 15:36, 22 декабря 2017
Задача 38.31 из сборника задач Мещерского Задача: С помощью языка программирования JavaScript смоделировать систему состоящую из двух конусов и ползуна скользящему по основанию одного из них.
Содержание
Реализация при помощи JS[править]
Используемые библиотеки[править]
- three.js
- stats.js
- dat.gui.js
Условия задачи[править]
Круговой конус с углом при вершине равным прикреплён к неподвижному конусу с углом при вершине равным шарниром и катится без скольжения. При этом ось конуса совершает вокруг вертикальной оси один оборот в секунду. Вдоль диаметра основания конуса проложена направляющая, по которой скользит ползун , совершая колебания около центра по закону . В начальный момент времени направляющая в одной вертикальной плоскости с шарниром . Найти модуль абсолютного ускорения ползунка в момент .
Решение[править]
, см. При точка совпадает с точкой
См. также[править]
Проектная деятельность по информатике