Мещерский 48.37 — различия между версиями

Материал из Department of Theoretical and Applied Mechanics
Перейти к: навигация, поиск
 
(не показано 7 промежуточных версий этого же участника)
Строка 1: Строка 1:
 +
== Условия задачи ==
 +
По наклонной плоскости скользит призма, к которой посредством цилиндрического шарнира и крутильной пружины присоединен тонкий стержнень.
 +
 +
== Реализация ==
 +
 +
'''Модель предусматривает изменение входных параметров:'''
 +
* Высота и длина платформы
 +
* Масса, длина, жесткость, начальный угол и начальная угловая скорость стержня
 +
* Масса, скорость и начальное положение скатывающейся призмы
 +
 +
Окно профильной проекции кликабельно и может изменяться по размеру для удобства просмотра.
 +
Полноэкранный режим доступен [http://tm.spbstu.ru/htmlets/Degterev/WebGL/pr/interface.html по ссылке].
 +
 +
{{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Degterev/WebGL/pr/interface.html |width=1000 |height=600 |border=0 }}
  
 +
== Используемые библиотеки ==
 +
* '''three.min.js'''
 +
* '''OrbitControls.js'''
 +
* '''dat.gui.min.js'''
 +
* '''stats.js'''
  
−
== Условия задачи ==
+
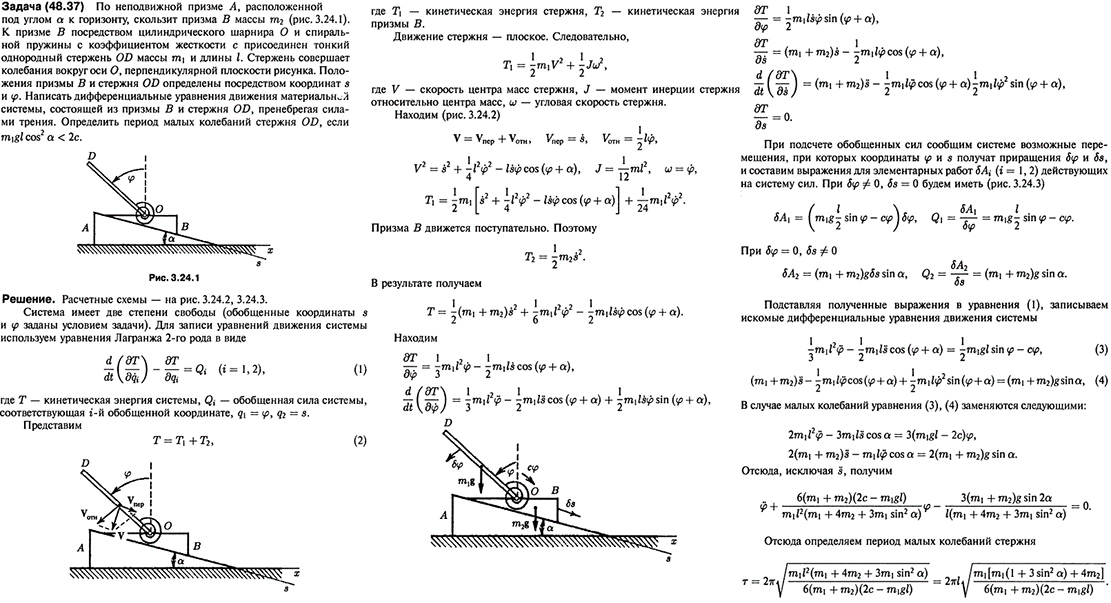
== Подробное решение ==
 +
[[File:M48373.png|frame|none]]
  
−
По неподвижной призме A, расположенной под углом α к горизонту, скользит призма В массы m2. К призме B, посредством цилиндрического шарнира O и спиральной пружины с коэффициентом жесткости c, присоединен тонкий однородный стержень OD массы m1 и длины l. Стержень совершает колебания вокруг оси O, перпендикулярной плоскости рисунка. Положения призмы В и стержня OD определены посредством координат s и φ. Написать дифференциальные уравнения движения материальной системы, состоящей из призмы В и стержня OD, пренебрегая силами трения. Определить период малых колебаний стержня OD, если m1gl cos2α< 2с.
 
−
== Решение ==
 
−
[[File:M4837.png|frameless]]
 
  
−
== Реализация ==
+
[[Дегтерев Данил]], 2017.
−
{{#widget:Iframe |url=http://tm.spbstu.ru/htmlets/Degterev/WebGL/pr/interface.html |width=1200 |height=700 |border=0 }}
 

Текущая версия на 21:01, 19 декабря 2017

Условия задачи[править]

По наклонной плоскости скользит призма, к которой посредством цилиндрического шарнира и крутильной пружины присоединен тонкий стержнень.

Реализация[править]

Модель предусматривает изменение входных параметров:

  • Высота и длина платформы
  • Масса, длина, жесткость, начальный угол и начальная угловая скорость стержня
  • Масса, скорость и начальное положение скатывающейся призмы

Окно профильной проекции кликабельно и может изменяться по размеру для удобства просмотра. Полноэкранный режим доступен по ссылке.

Используемые библиотеки[править]

  • three.min.js
  • OrbitControls.js
  • dat.gui.min.js
  • stats.js

Подробное решение[править]

M48373.png


Дегтерев Данил, 2017.

Источник — «http://tm.spbstu.ru/?title=Мещерский_48.37&oldid=49239»